Әдебиеттер [4] І тарау § 1,§ 2, [5], [6] I тарау, 1.,2.,3., [7] 1-тарау
Егер жазықтықта салу есебі төмендегі салу постулаттарына келтірілген болса, онда есеп циркуль мен сызғыштың жәрдемімен шешілген болып есептеледі:
1. Берілген екі нүкте арқылы түзу жүргізуге болады.
2. Егер центр және радиус берілсе, онда шеңбер салуға болады.
3. Берілген екі түзу параллель болмаса, онда олардың қиылысу нүктесін салуға болады.
4. Берілген түзу мен берілген шеңбердің қиылысу нүктелерін (егер олар бар болса) салуға болады.
5. Берілген екі шеңбердің қиылысу нүктелерін (егер олар барболса) салуға болады.
6. Жазықтықтың кез келген нүктесін салуға болады.
Циркульдің ашасын ашып, оның жәрдемімен кез келген радиуспен шеңбер салуға, ал сызғыш бір жақты және онымен ұзындығы шектеусіз түзу сызықтар жүргізуге болады деп есептеледі.
Салу есептерін шығарудың негізгі әдістері:
1. Нүктелердің геометриялық орындар (НГО) әдісі.
2. Геометриялық түрлендірулер әдісі.
3. Алгебралық әдіс.
Қарапайым НГО:
1. Берілген О нүктесінен берілген r қашықтықта жатқан НГО - шеңбер.
2. Белгіленген екі нүктеден бірдей қашықтықта жатқан НГО – кесіндінің орта перпендикуляры.
3. Берілген түзуден d қашықтықта жатқан НГО - түзуден d қашықтықтағы параллель екі түзу.
4. Берілген параллель екі түзуден бірдей қашықтықта жатқан НГО – екі параллель түзулер ара қашықтығының ортасынан жүргізілген оларға параллель түзу.
5. Бұрыштың қабырғаларынан бірдей қашықтықтағы НГО – бұрыштың биссектрисасы.
6. а кесіндісі берілген бұрышпен көрінетін НГО салу.
7. Берілген кесінді тікбұрышпен көрінетін НГО – кесіндінің ортасын центр етіп радиусы кесіндінің жартысына тең жарты шеңбер.
НГО табуға берілген есептерді шығару әдетте талдаудан, салудан дәлелдеуден, зерттеуден құралады.
Салынған НГО дәлелдеу өз ара кері мынадай екі сөйлемнің дұрыс екендігін айқындауға келіп тіреледі.
а) НГО мінездемелік қасиетіне ие болатын кез келген М нүктесі табылған фигураға тиісті;
б) егер нүкте табылған фигураға тиісті болса, онда ол іздеп отырған НГО мінездемелік қасиетіне ие болады.
НГО іздегенде фигураның мінездемелік қасиетке ие болатын барлық нүктелерінің жиынын табу қажет. Егер мінездемелік қасиетке ие болатын нүктелердің табылған фигурадан тыс фигурада жатпайтындығына көзімізді жеткізсек, онда табылған фигураны іздеген НГО деп санай аламыз.
Сондай-ақ, жоғарыда келтірілген екі сөйлемнің әрқайсысын дәлелдеуді оларға эквивалентті мынадай сөйлемдерді дәлелдеумен алмастыруға болатындығын байқаймыз:
а) егер М нүктесі табылған фигурада жатпайтын болса, онда ол нүкте іздеп отырған НГО мінездемелік қасиетіне ие болмайды;
б) егер М нүктесі іздеп отырған НГО мінездемелік қасиетіне ие болмаса, онда ол нүкте табылған фигурада жатпайды.
НГО табу есептерін шығарайық:
1-есеп. Берілген АВ кесіндісі тік бұрышпен көрінетін НГО табу керек.
Шешуі. 1-тәсіл. АВ кесіндісі М нүктесінен тік бұрышпен көрінеді делік (1-сурет).
| М |
| В |
| О |
| А |

|

|

|
| 1-сурет |
 AMO=
AMO=  MAB=α бұрышын салайық, сонда
MAB=α бұрышын салайық, сонда 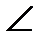 OMB=
OMB= 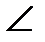 MBO=
MBO= 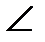 β=900-α. АОМ және МОВ — тең бүйірлі үшбұрыштар, олай болса, АО= ОМ=ОВ, яғни ОМ =
β=900-α. АОМ және МОВ — тең бүйірлі үшбұрыштар, олай болса, АО= ОМ=ОВ, яғни ОМ = 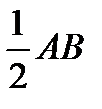 . Сонымен, М нүктесі берілген кесіндінің ортасынан тұрақты шама-
. Сонымен, М нүктесі берілген кесіндінің ортасынан тұрақты шама- 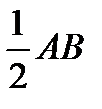 -ге тең кашықтықта жатады, олай болса, М нүктесі центрі О және радиусы r =АВ: 2 болатын шеңбердің бойында жатады.
-ге тең кашықтықта жатады, олай болса, М нүктесі центрі О және радиусы r =АВ: 2 болатын шеңбердің бойында жатады.
Кері сөйлем де дұрыс болады. Нүкте табылған шеңберде жатады делік, олай болса, шеңберге іштей сызылған және диаметрге тірелген бұрыш болғандықтан, 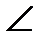 АМВ = 90° болады. Бұдан мынадай қорытынды жасаймыз: шеңбердің А және В нүктелерінен басқа кез келген М нүктесінен қарағанда АВ кесіндісі тікбұрышпен көрінеді.
АМВ = 90° болады. Бұдан мынадай қорытынды жасаймыз: шеңбердің А және В нүктелерінен басқа кез келген М нүктесінен қарағанда АВ кесіндісі тікбұрышпен көрінеді.
Сонымен, берілген АВ кесіндісі тікбұрышпен көрінетін НГО — А және В нүктелерін есептемегендегі, диаметрі АВ болатын шеңбер.
Егер М 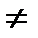 А және М
А және М 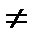 В болып, М нүктесі шеңбердің бойында жатса, онда
В болып, М нүктесі шеңбердің бойында жатса, онда 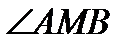 = 90° болады. Егер М шеңбердің ішінде немесе шеңберден тыс жатса, онда
= 90° болады. Егер М шеңбердің ішінде немесе шеңберден тыс жатса, онда 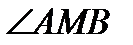
 90° болады (төбесі дөңгелектің ішінде және дөңгелектен тыс жатқан бұрыштардың қасиеті бойынша). Осы себептен іздеп отырған НГО жоғарыда табылған НГО - бірдей болып келеді.
90° болады (төбесі дөңгелектің ішінде және дөңгелектен тыс жатқан бұрыштардың қасиеті бойынша). Осы себептен іздеп отырған НГО жоғарыда табылған НГО - бірдей болып келеді.
2 - т ә с і л. АВ кесіндісі М нүктесінен тікбұрышпен көрінеді делік (2-сурет).
М нүктесін АВ кесіндісінің О ортасымен қосып, ОМ түзуінің бойына ОМ = ОД кесіндісін салайық. АД және ВД кесінділерін жүргізейік.
| М |
| В |
| O |
| D |
| А |
| К |
| 2-сурет |
АМВД төртбұрышы — тіктөртбұрыш, олай болса, ДМ=АВ; бұдан ОМ= 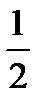 АВ = ОА = ОВ екендігі шығады. Сонымен, М нүктесі центрі О нүктесі және радиусы ОМ=
АВ = ОА = ОВ екендігі шығады. Сонымен, М нүктесі центрі О нүктесі және радиусы ОМ= 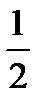 АВ болып келген шеңбердің нүктесі болады.
АВ болып келген шеңбердің нүктесі болады.
Кері сөйлемнің дұрыстығын дәлелдеу есепті шешудің бірінші тәсілін қарастырғанда берілген.






