53-есеп. Үшбұрышты пирамиданың бүйір жақтарының бірі табан жазықтығына перпендикуляр. Осы бүйір жағы мен табаны дұрыс үшбұрыштар. Пирамиданың кескіні ретінде диагоналдармен қоса алынған ABCD төртбұрышын алып, кескіннің параметрлер санын анықтайық.
Шешуі: Пирамида табанындағы дұрыс үшбұрыштың кескіннің кез келген үшбұрыш болып алынуынан екі параметр жаратылады (84-сурет).
Нақтырақ айтсақ, мұнда АВ=ВС=АС және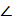 
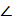A= B= 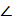C метрикалық қасиеттері сақталмай отыр. Осы сияқты бір бүйір жағының да дұрыс үшбұрыш екендігін ескерсек, оған да екі параметр жаратылады және осы салынған үшбұрыштардың жазықтықтары түпнұсқада перпендикуляр екендігін ескерсек, кескінге тағы да бір метрикалық шарт қойылады, яғни тағы бір параметр жаратылады. Олай болса, берілген пирамиданың кескініне бес параметр жаратылған, яғни кескіннің параметрлік саны р=5, сондықтан бұл кескінде бұлардан басқа ешқандай метрикалық салуларды еркін орындауға болмайды. Енді осы SABC пирамиданың кескінінде SAC жағының SK биіктігін салу қажет болсын. Ол үшін қосымша салулар жүргізу қажет. ABC үшбұрышының BN медианасын жүргіземіз.
Сурет-84
ABC дұрыс үшбұрыш болғандықтан BN әрі биіктік болады, яғни BN┴ АС. Осыған ұқсас SAB үшбұрышының SD медианасын, әрі биіктігін жүргіземіз. Мұндағы SD┴AB және SD┴ (ABC). DK||BN жүргіземіз, сонда DK┴AC болады. S нүктесі мен К нүктесін кесіндімен қосамыз. SD кесіндісі ABC жазықтығына перпендикуляр болғандықтан, DK оның ABC жазықтығындағы проекциясы және DK ┴ АС екендігін ескерсек үш перпендикуляр туралы теорема бойынша SK┴ АС болатындығын көреміз.
Сурет-85
Міне көріп отырғанымыздай, SK биіктігінің табаны К нүктесі АС қабырғасының бойынан жалғыз түрде анықталады, демек SK биіктігі де жалғыз түрде анықталып отыр.
54-есеп. Сызбада берілген ABC үшбұрышы тең қабырғалы үшбұрыштың кескіні болып табылады. Осы үшбұрышқа сырттай сызылған шеңбердің кескінін салу қажет (85-сурет).
Шешуі. AN, ВМ, CL медианаларын жүргіземіз. ABC дұрыс үшбұрыш болғандықтан бұл медианалар әрі биіктік, әрі биссектриса да болып табылады. AО=2ОN=r екендігін ескеріп, AN түзуіне ND=ON, ВМ медианасының созындысына MF=OM, CL медианасының созындысына TL=OL кесінділерін өлшеп саламыз. Осы A, Ғ, С, D, В, Т нүктелері арқылы ізделінді шеңбердің кескінін жүргіземіз.
Бұл мысалды шығара отырып, тең қабырғалы үшбұрыш кескіні ретінде кез келген үшбұрышты алуға болатындығына көз жеткізілді. Үшбұрыштың кескіні таңдалып алынғаннан соң, оған сырттай сызылған шеңбердің кескіні толық анықталды, Алынған қорытынды мен бұрынғы тәсілдерді байланыстыра отырып дұрыс үшбұрыш кескіні де бейнелеу жазықтығындағы кескіннің метрикасын анықтайтындығын көреміз.
55-есеп. Сызбада шеңбердің кескіні берілген. Осы шеңберге сырттай сызылған тік бұрышты үшбұрыштың кескінін салу керек (86-сурет).
Шешуі: Эллипстің MN және KL өзара түйіндес диаметрлерін жүргіземіз. К және М нүктелері арқылы эллипске жанамалар жүргіземіз, олар сәйкесінше өзара түйіндес MN, KL диаметрлеріне параллель болады. Сондықтан бұл жүргізілген жанамалар да өзара перпендикуляр түзулердің кескіндерін береді.
Шындығында, шеңбердің АС жанамасына ОМ радиусы немесе MN диаметрі перпендикуляр болуы керек. Ал есеп шешімі бойынша MN және KL өзара перпендикуляр диаметрлер. Олай болса, AC ┴KL болуы керек, ал кескіндеу барысында олардың параллельдігі сақталады. Дәл осылай ВС мен MN параллелдігінде дәлелдеп көрсетуге болады.
Үшбұрыштың гипотенузасын кескіндеу үшін эллипске үшінші жанама жүргізіледі.
Сурет-86
Көпбұрышты пирамиданың кескінін салу
Көпбұрышты пирамидалардың кескінін салу техникасы да, үшбұрышты пирамиданың кескінін салу тәсіліне ұқсас орындалады. Пирамида түпнұсқасынан базистік нүктелер ретінде оның төбелері алынады. Үшеуі оның табанынан алынады, төртінші нүкте пирамиданың төбесі болады.
Үшбұрышты пирамиданың кескінін салғандағыдай түпнұсқаның базистік төрт нүктесінің кескінін бейнелеу жазықтығында бірден белгілеп алу тиімсіз болады. Пирамиданың төбесінің кескіні болатын S базистік нүктесін, пирамида табанын, одан кейін пирамида биіктігін кескіндегеннен соң барып салған дұрыс.
56-есеп. SABCD пирамидасы берілген. ABCD тең бүйірлі трапеция. SAB бүйір жағы тең бүйірлі үшбұрыш және табан жазықтығына перпендикуляр. Осы пирамиданың кескінін салу керек.
Шешуі: Табанындағы ABCD тең бүйірлі трапециясының кескінін кез келген трапеция етіп саламыз. Түпнұсқада пирамида биіктігі табанының АВ қырының ортасына түседі. Олай болса, АВ қырының кескінінің ортасы Н нүктесін анықтаймыз.
Сурет-87
Осы нүктеден HS вертикаль кесіндісін тұрғызамыз. S нүктесінен пирамида табанындағы трапеция төбелерін кесінділер арқылы қосып, ізделінді пирамиданың кескінін аламыз. Яғни, мына жоғарыдағы 87- суреттегі ретпен орындалады.
Призманың кескінін салу
Базистік нүктелер ретінде призманың төбелерін ала отырып, призманың кескінін оңай салуға болады. Оның үшеуін бір табанынан, ал төртіншісін басқа табанынан аламыз. Базистік нүктелердің үшеуін призманың төменгі табанындағы көпбұрыштың төбелері етіп таңдап ала отырып, бірінші кезекте бейнелеу жазықтығында оның табанының кескінін салып аламыз. Төртінші базистік нүктесін призманың жоғарғы табанынан таңдап алып, оны бейнелеу жазықтығында ыңғайлы түрде кескіндей отырып призманың оңай орындалатын және көрнекі түрдегі дұрыс кескінін аламыз. Яғни, ол фигура кескініне қойылатын барлық негізгі үш талапты қанағаттандыратын болады [31].
57-есеп. Табаны а және биіктігі һ болатын дұрыс үшбұрышты тік призманың кескінін салу керек.
Шешуі. A'B'С'A11B1'C11дұрыс үшбұрышты призмасы берілген болсын. Призманың төменгі табанындағы A1B1C1 дұрыс үшбұрышының төбелерін базистік нүктелер етіп ала отырып, бейнелеу жазықтығында “Бар болудың бірінші теоремасы” негізінде кез келген ABC үшбұрышын саламыз (88,a - сурет). Ал, төртінші базистік нүктені призманың А11 төбесі етіп аламыз. Оның бейнелеу жазықтығындағы кескінін салу үшін А нүктесінен АА1 вертикаль кесіндісін жүргіземіз (88, ә - сурет). Осы ретпен призманың төрт базистік нүктесінің кескіні еркін түрде салынғаннан соң басқа төбелерінің кескіндерін еркін түрде салуға болмайды. Өйткені, “Бар болудың екінші теоремасы” негізінде төрт базистік нүктені кескіндей отырып бейнелеу жазықтығындағы барлық нүкте бір мәнді анықталады. Шындығында, A'B'С'A11B1'C11 призманың түпнұсқасында A'A11,
B'B1', C1C11, бүйір қырлары өзара параллель, әрі тең. Олай болса, призма кескініндегі сәйкес АА1, ВВ1, СС1 қырларыда өзара параллель, әрі тең болуы керек. Демек, призманың кескіні одан әрі мына ретпен салынады: В және С нүктелері арқылы AA1 кесіндісіне параллель түзулер жүргізіліп, оның бойына АА1 кесіндісіне тең ВВ1 және СС1 кесінділері өлшеніп салынады. А1, В1, С1 нүктелерін кесінділермен қосып дұрыс үшбұрышты призманың кескінін аламыз (88, б - сурет) [32].
Сурет-88
ҚОРЫТЫНДЫ
Есептерді геометриялық әдіспен шешкенде логикалық ойлаудың жәрдемімен белгілі теоремалар арқылы тұжырымдауды қажет ететін сөйлемдерді дәлелдейміз.
Геометриялық салу — кейбір геометриялық есептерді абсолют дәл деп ұйғарылатын әр түрлі аспаптардың (сызғыштың, циркульдің, тағы басқа) көмегімен шығару.
Есептердің түрі аспаптардың таңдап алынуына тәуелді болады. Салу есептері циркуль мен сызғыштың көмегімен, ізделініп отырған нүктелердің координаттары операциялар (қосу,көбейту, бөлу және квадрат түбір табу) саны шекті болып келген өрнек түрінде жазылса ғана шығарылады. Егер мұндай өрнек табылмаса, онда салу есебін циркуль мен сызғыштың көмегімен шығаруға болмайды. Мысалы, мұндай есептерге кубты екі еселеу, бұрыштың трисекциясы, дөңгелек квадратурасы жатады. Циркуль мен сызғыштың көмегімен шығарылатын кез келген салу есебін бір ғана циркульмен не сызғыштың (кейде бұрыштықпен) өзімен де шығаруға болады.
Жұмысты қорытындылай келе келесі ұсыныстарды беруді жөн санадық.
Әдістемелік ұсыныстар:
1. Салуға берілген есепті шешуге кірісуден бұрын материалдың теориялық жағын меңгеріп алу қажет.
2. Салу есептерін шешуге кіріскенде алдымен қарапайым салулардан бастап шешу керек.
3. Есептер шешу кезінде әсіресе көрнекі құралдар мен модельдерді (нұсқаларды) пайдаланудың ерекше маңызы бар.
4. Негізгі салуларды дәл орындау керек:
а) кеңістіктегі нүктенің орнын анықтау;
б) берілген екі нүкте арқылы түзу жүргізу;
в) бір түзудің бойында жатпайтын үш нүкте арқылы жазықтық жүргізу;
г) түзу мен жазықтықтың қиылысу нүктесін табу;
д) әрбір жазықтықта барлық планиметриялық салулардың орындалуы;
е) егер өзін анықтайтын элементтер берілсе, онда геометриялық дене салу.
Егер кеңістікте салуға берілген есептердегі негізгі амалдар, яғни онда ұсақ бөліктерге бөлінетін негізгі қарапайым салулар түгел орындалса, онда кеңістіктегі кез-келген геометриялық салу орындалады деп есептеледі.
Геометриялық ұқсас түрлендіру әдісінің мәнісі, геометриялық есептерді шығару кезінде сай келетін геометриялық өзгертулерді пайдалану керек, оның қасиеттеріне сүйенгенде есеп шығаруға мүмкіндік береді.
Түрлендіру әдістерімен есептер шығару үшін, осы әдіс компоненттерін падалана блуіміз керек:
§ кез-келген түрлендіруде фигуралар бейнелерін жасай білу;
§ сай келетін фигураларда өзгертетін фигуралардың нүктелерін көре білу;
§ белгілі бір түрлендіруді анықтайтын элементтерді айқындай білу (ось немесе симметрия центрі, центр және айналу бұрышы, параллель көшіру векторы, гомотетияның центрі мен коэффициенті т.б.);
§ түрлендіруде сай келетін нүктелерді сай келмейтін фигураларға сала білу.
Ескеру керек, бір геометриялық есепті шығарған кезде, базалық фигураның ерекшелігін және оның ізделінуші элементтредің арасындағы осы фигаремен байланысын есепке ала отырып орындау керек. Ал дұрыс таңдай жасай білу, ереже бойынша, есепті рационалды шығаруға мүмкіндік береді. Бұл жерде түрлендіруді таңдауда базалық фигураның формасы мен қасиеті мағызды болып табылады. Симметрияны тек базалық фигураның симметриялық центрі (параллелограм, шеңбер және т.б.) немесе симметриялық өсі (түрліқабырғалы бұрыш,түрліқабырғалы трапеция, шеңбер т.б.) болған кезде жүргізген дұрыс. Айналуға базалық фигура бұрылмалы қасиетке ие болғанда жүргізіледі (дұрыс үшбұрыш, квадрат, дұрыс алтыбұрыш, шеңбер т.б.). Есептерде қозғалысты қолданған кезде, бүкіл фигураның түрленуін емес, оның кейбір бөліктерін қарастыруға да болады (трапецияның бір бүйірін көшіру немесе негіздердің бірімен анықталатын диагональдарының бірін векторға ауыстыру).
Гомотетия есептерінде екі базалық фигура гомотетия центрі болып табылуы керек (параллель жақтары бар екі үшбұрыш, түрлі радиустағы екі шеңбер т.б.). Гомотетия мен ұқсастықты пайдалана есептерді шығарған кезде мына амлдар жиі қолданылады: талдама жасау кезінде берілген сызықтық элементтерді алып тастау керек немесе берілген фигуралардың біразын ескермей-ақ қою керек(бір нүктелер позициясын) және құрылымды фигураның қалған бөліктерінің позициясы арқылыжасауға болады, сонан соң ғана алынып тасталған элементті қайта қоюға болады.
Жазықтық инверсиясын түрлендіру, оның сызықтық болмауына қарамастан, қатарлауға геометриялық есептер шығаруда қолдануға болады. Инверсияны қолдану арқылы конструктивті есептер шығару кезінде негізгі идея, сәтті инверсияны таңдау, атап айтқанда – түрлендірген фигурамен есептер шығару оңай болып, қажетті нәтиже жақсы алынады.
Сонымен, біз ұқсас түрлендіру әдістерімен есептер шығару есеп шартарының егжей-тегжей талқылануын және түрлендіруді таңдауға сауатты кһз-қараспен қарап, асықпай шешім қабылдау қажет: 1) есеп шартын асықпай талдап, базалық фигураны таңдап алу қажет; 2) түрлендіруді таңдау барысында, алдын-ала оны құрайтын барлық элементтерді түгелдеп алу керек; 3) түрлендіру қасиеттерін еске түсіріп, оларды есеп шығаруда қолдана білу керек; осыдан кейін ғана есеп шығаруға кіріскен жөн.
Әрине ұтымды түрлендіру түрін таңдау, геометриялық ұқсас түрлендіру есептерін шығаруда көп тәжірибе мен білімді қажет етеді.
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
1. Программа для базового образования школ Казахстана» Алматы: Министерство образования РК 1992
2. Программа для школ с углубленным изучением математики Алматы: Министерство образавания РК 1994
3. Абілқасимова А.Е., Көбесов А.К., Рахымбек Д.Р., Кенеш Ә.С. «Математиканы оқытудың теориясы мен әдістемесі» Алматы «Білім» 1998
4. Атанасян Л.С. және т.б. «Геометрия» Алматы 1992
5. Алдамұратова Т.А., Байшоланов Е.С. Математика. Оқыту әдістемесі. Алматы. Атамұра. 2005
6. Аргунов Б.И., Балк М.Б. Жазықтықта орындалатын геометриялық салулар. Алматы 1955
7. Бекбоев И.Б. және т. б., «Геометрия» Алматы Мектеп. 2007
8. Бекбоев И., Абдиев А «Геометрия» 7,8,9-сыныптарына арналған оқулық. А., Мектеп. 2008
9. Бекбоев И., Абдиев А., Қайдасов Ж., Хабарова Ғ. «Геометрия» 8-сынып. А., Мектеп. 2008
10. Бабанский Ю.К. «Выбор методов обучения в средней школе» Москва 1989
11. Бидосов Ә. «Математиканы оқыту методикасы» Алматы 1989
12. Богоявлинский Д.Н., Менчинская Н.А. «Психология усвоения знаний в школе» Москва 1959
13. Волович М.В. «Математика без перегрузок» Москва 1991
14. Гусев В. А., Мордкович А. Г. «Математика» Москва 1990
15. Давыдов В.В. «Проблемы развивающегося обучения» Москва 1986
16. Жүнісов Т.А., Планиметриялық салу есептерін шығару әдістері. Алматы 1998
17. Жұбаев Қ., Геометрияны оқыту әдістемесі. Алматы. РБК. 1992
18. Мадияров Н.К. Геометриялық фигураларды кескіндеу. Оқу құралы.Шымкент.М. Әуезов атындағы ОҚМУ. 2010
19. Мишин В. И. «Методика преподавания математики в средней школе» Москва 1987
20. Мордкович А. Г. «Методические проблемы изучения тригонометрии в общеобразовательной школе» Москва 2002
21. Мұханов М. «Жас және педагогикалық психология» Алматы 1981
22. Көбесов А. «Орта мектепте математиканы оқыту методикасы» Алматы 1989
23. Көбесов А. «Математика тарихы» Алматы 1997
24. Қайдасов Ж., Хабарова Ғ., Абдиев А., «Геометрия» 8-сынып. А., Мектеп. 2008
25. Лернер И.Я. «Процесс обучения и его закономерности» Москва 1980
26. Лернер И.Я. «Дидактические основы методов обучение» Москва 1981
27. Погорелов А.В. «Геометрия» Жалпы білім беретін мектептің 7-11 сыныптарына арналған оқулық. Алматы. Просвещение-Қазақстан. 2003
28. Рахымбеков Д., Кенешев Ә. «Математикалық ұғымдарды оқыту» Жезқазған 1997
29. Рахымбеков Д. «Оқушылардың логика – методологиялық білімдерін жетілдіру» Алматы 1998
30. Рахымбек Д., Кенеш Ә. Мектеп геометрия (планиметрия) курсын оқыту әдістемесі. Оқу құралы. А. Эверо. 2015
31. Рахымбек Д., Кенеш Ә. Мектеп геометрия (стереометрия) курсын оқыту әдістемесі. Оқу құралы. А. Эверо. 2015
32. Рахымбек Д.,Мадияров Н.К. Геометриялық салу есептері. Оқу құралы. А. Эверо. 2015
33. Рыжик В.И. «Геометрия» Москва 1992
34. Слепкань З.И. «Психолого – педагогические основы обучения математике» Киев 1983
35. Столяр А.А. «Педагогика математики: Учеб.пособие для физ-мат фак.пед.ин-тов» Минск 1986
36. Шыныбеков Ә.И., «Геометрия» 7-сынып. А., Атамұра. 2007
37. Шыныбеков Ә.И., «Геометрия» 9-сынып. А., Атамұра. 2007
38. Шамова Т.И. «Активизация учения школьников» Москва 1982
39. С.Е. Шәкілікова, С.Ш.Жақсымбетова «Геометрия есептері» Алматы1995
40. Эрдниев П.М., Эрдниев Б.П. «Укрупнение дидактических единиц в обучении математике» Москва 1986
41. Юсупов Ж., Зәуірбеков С.С., Геометрия. Жалпы білім беретін мектептің 7,8.9 сыныптарына арналған байқау оқулығы. Алматы. Рауан.2000
Осымша А
Сабақ жоспары (үлгі ретінде)
| 08.12.201ж | Геометрия | 9 сынып | |||
| Сабақтың тақырыбы: | «Ұқсастық түрлендіру және оның қасиеттері. Ұқсас фигуралар» | ||||
| Сабақтың мақсаты: | Білімділік: Ұқсас түрлендіру, гомотетия, гомотетия центрі, гомотетия коэффиценті, гомотетия қасиеттерін түсінеді. Дамытушылық: Гомотетиямен байланысты тапсырмаларды орындау дағдысын меңгеріп, фигуралардың гомотетиялығын анықтау, есептер шығаруға дағдыланады. Тәрбиелілік: Сызба сызуда сызу сабағының элементтерін пайдалануға, ұқыптылыққа тәрбиелеу. | ||||
| Күтілетін нәтиже | 1. Қозғалыстың түрлерін меңгере отырып, ұқсастық түрлендіруі ұғымымен танысады және фигураларды түрлендіру тәсілін анықтауды үйренеді. 2. Есеп шығарудағы қабілеттілігі артады. 3. Бір – бірімен ақылдасады. | ||||
| Сілтеме | 9 сынып «Геометрия» оқулығы | ||||
| Сабақта қолданылатын материалдар: | Слайд Оқулық Тақырыпқа байланысты көрнекіліктер | ||||
| Оқыту әдістері: | 1. Жеке жұмыс 2. Жұптық жұмыс | ||||
| Сабақтың барысы. І.Ұйымдастыру кезеңі | 1. Сәлемдесу, түгендеу 2. Оқушылардың зейінін сабаққа аудару 3. Сабақ барысымен таныстыру, жұпқа бөлу | ||||
| ІІ.Үй тапсырмасын тексеру | Миға шабуыл сұрақтары | ||||
| ІІІ. Жаңа сабақ | Жаңа тақырыпты түсіндіру | ||||
| ІҮ. Тапсырма | Тест жұмысы | ||||
| Ү. Сергіту сәті | Тренинг ұйымдастыру | ||||
| Ү. Қорытынды | Жаңа тақырып бойынша сұрақтар қойылады. | ||||
| ҮІ. Үй тапсырмасы | Оқулық № 57-59 есептер | ||||
Сабақ бойынша мұғалім мен оқушының іс-әрекеті:
| Мұғалімнің іс-әрекеті | Оқушының іс-әрекеті | |
| І. Ұйымдастыру кезеңі 5 минут | Оқушылардың зейінін сабаққа аудару, түгендеу, жұпқа бөлу ББҮ үлестірме қағазын таратып беру | Оқушылар жұптарға бөлінеді. |
| ІІ.Үй тапсырмасын тексеру Миға шабуыл сұрақтары 10 минут | Әр қасиеттерін атаңдар | Оқушылар жұппен ақылдасып, сұрақтарға жауап береді. |
| ІІІ. Жаңа сабақ 5 минут | Анықтама. Егер Ф фигурасын Ф1 фигурасына бейнелегенде, олардың сәйкес нүктелерінің арақашықтықтары бірдей к қатынасына өзгеретін болса, онда Ф фигурасын Ф1 фигурасына ұқсас деп атаймыз. Анықтама. Жазықтықтағы әрбір А нүктесі үшін ОА сәулесінің бойында жататын және ОА1/ОА=к шартын қанағаттандыратын А1 нүктесін А нүктесіне гомотетиялы нүкте деп атаймыз. Ал жазықтықтың бұл түрлендіруін гомотетия деп атайды. | Оқушылар сабақты мұқият тыңдайды. Қажетті мәліметтерді дәптерлеріне жазып алады. |
| ІҮ. Тапсырма 15 минут | Тест жұмысы
1.  . а) АВ және СD кесінділері гомотетиялы бола ма?
ә) Гомотетия коэффициенті қандай?
A. а) болады; ә) 
B. а) болады; ә) 
C. а) болмайды; ә) 
D. а) жауабы өзге.
2.  ді табыңдар.
A. 
B. 
C. 
D. 
3.  мен  -ді табыңдар.
A. 
B. 
C. 
D. жауабы өзге
4.  -ның периметрін табыңдар.
A. 12 см
B. 13 см
C. 14 см
D. 15 см
5.  және тең бүйірлі үшбұрыштар.  -ны табыңдар.
A. 
B. 
C. 
D. 
6. , АВС үшбұрышының периметрі 42 см, ал  -дің периметрі 14 см және  АВ-ны табыңдар.
A. 13 см
B. 14 см
C. 15 см
D. 16 см
| Тест жұмысын орындап, жұппен тексереді, дәптерлеріне жазып алады. |
| Ү. Қорытынды 5 минут | 1. Қандай фигураларды ұқсас фигуралар деп атайды? 2. Ұқсастық коэффициенті деп қандай санды айтады? | Сұрақтарға жауап береді. |
| ҮІ.Үй тапсырмасы 2 минут | §4 оқу.Анықтамалар жаттау. | Тапсырмаларды мұқият тыңдап, түртіп алу |
| ҮІІ. Бағалау 3 минут | Білемін Білгім келеді Үйрендім Сабақ барысында алған баллдарын қорытып, бағалау | Сабақта алған бағаларын күнделіктеріне қойдыру. |
Осымша В
Өзіндік жұмыс үшін планиметриядағы ұқсас түрлендіруге берілетін есептердің үлгілері
1. Гомотетия арқылы X нүктесі X' нүктесіне, ал Ү нүктесі Ү' нүктесіне көшеді. Егер X, X', Ү, Ү' нүктелері бір түзудің бойында жатпаса, гомотетия центрін қалай табуға болады?
2. Гомотетия арқылы X нүктесі X' нүктесіне көшеді. Гомотетия коэффициенті 2-ге тең деп алып, гомотетия центрін салып көрсетіңдер.
3. Үшбұрыш сызыңдар. Оның төбелерінің бірін гомотетия центрі деп алып және де гомотетия коэффициенті 2-ге тең деп есептеп берілген үшбұрышқа гомотетиялы үшбұрыш салыңдар.
4. 2.4-суретте 1: 1000 масштабпен үй маңының жоспары кескінделген. Оның өлшемдерін (ұзындығы мен енін) анықтаңдар.
5. Үшбұрышқа ұқсас фигура не болып табылады?
6. Ұқсас ABCжәне А1В1С1 үшбұрыштарының 
A = 30°, АВ = 1 м, ВС = 2 м, В1С1= 3 м. A1 бұрышы мен А1В1 қабырғасы неге тең?
7. Шеңберге ұқсас фигура да шеңбер болатынын дәлелдеңдер.
8. Бұрыш берілген және де оның ішінен А нүктесі белгіленген. Бұрыштың қабырғаларын жанап және де берілген А нүктесінен өтетін шеңберді салыңдар.
9*. Берілген үшбұрышқа іштей квадрат сызыңдар, сонда мұның екі төбесі бір қабырғаның бойында жатсын да, ал қалған екі төбесі былайғы екі қабырғаның бойында жататын болсын.
10. Табандарына қарсы төбелеріндегі бұрыштары бірдей тең бүйірлі үшбұрыштардың ұқсас болатындығын дәлелдеңдер.
11. Тең бүйірлі екі үшбұрыштың бүйір қабырғаларының арасындағы бұрыштары тең. Бір үшбұрыштың бүйір қабырғасы мен табаны 17 см-ге және 10 см-ге тең, екінші үшбұрыштың табаны 8 см-ге тең. Оның бүйір қабырғасын табыңдар.
12. ABC және А1В1С1 үшбұрыштарында: A = А\,
B= В1, AB= 5 м, BC =7 m, А1В1=10 м, А1С1= 8 m. Үшбұрыштардың қалған қабырғаларын табыңдар.
13. 12-есепте AВ =16 cm, ВС = 20 cm, А1В1= 12 cm. AC — А1С1 = 6 cm деп алып, оны қайта шығарыңдар.
14. Тік бұрышты үшбұрыштың тік бұрышының төбесінен түсірілген биіктігі оны соның өзіне ұқсас екі үшбұрышқа бөлетінін дәлелдеңдер.
15. ABC үшбұрышының АВ қабырғасына параллель түзу оның АСқабырғасын A1 нүктесінде, ал ВС қабырғасын В1 нүктесінде қиып өтеді. ABCмен А1В1С1 үшбұрыштары ұқсас екендігін дәлелдеңдер.
16. Табаны а және биіктігі һболатын үшбұрышқа іштей сызылған квадраттың екі төбесі үшбұрыш табанына, қалған екі төбесі бүйір қабырғаларға тірелген. Квадраттың қабырғасын есептеп шығарыңдар (В-1- сурет).
17. ABC үшбұрышының АВ қабырғасына параллель түзу оның АСқабырғасын, С төбесінен бастап есептегенде, т: п қатынасында бөледі. Ол түзу ВСқабырғасын қандай қатынаста бөледі?
18. ABC үшбұрышының АС қабырғасына параллель DE кесіндісі жүргізілген (кесіндінің D ұшы АВ қабырғасында, ал Е ұшы ВС қабырғасында жатыр). АВ=16 см, АС = = 20 см және DE = 15 см деп алып, AD кесіндісін
табыңдар.
19. 18-есепте AC:DE = 55:28 деп алып, AD'.BD қатынасын табыңдар.
20. Мына деректерді пайдаланып, 18-есептегі DEкесіндісінің ұзындығын табыңдар.
1) АС = 20 см, АВ = 17 см және BD = 11,9 см;
2) АС = 18 дм, AВ = 15 дм және AD = 10 дм.
21. ABCD трапециясының диагональдары Е нүктесінде қиылысады (В-2 - сурет). ВСЕ және DAE үшбұрыштарының ұқсас болатынын дәлелдеңдер.
22. Трапеция табандарының қатынасы т: п қатынасындай. Оның бір диагоналы екінші диагоналымен қиылысқанда шығатын кесінділердің қатынасын табыңдар.
Сурет В-1 Сурет В-2
23. Трапеция диагональдарының қиылысу нүктесінен өтетін түзу оның бір табанын т: пқатынасында бөледі. Ол түзу трапецияның екінші табанын қандай қатынаста бөледі?
24. АС диагоналы жүргізілген ABCDтрапециясында ABC және ACD бұрыштары тең. Трапецияның ВС мен AD табандары сәйкесінше 12 м-ге және 27 м-ге тең, АС диагоналын табыңдар.
25. Трапеция табандарына параллель түзу оның бір бүйір қабырғасын т:п қатынасында бөледі. Ол екінші бүйір қабырғаны қандай қатынаста бөледі?
26. ABCDтрапециясының бүйір АВ мен CD қабырғаларының созындылары Е нүктесінде қиылысады. АВ=5см, ВС = = 10 cm, CD = 6 cm, AD=15 cm, AED үшбұрышының қабырғаларын табыңдар.
27. 26-есепте ВС= 7 cm, AD = 21 см және трапецияның биіктігі 3 см деп алып,AED үшбұрышының биіктігін табыңдар.
28. *. Трапеция диагоналдары Е нүктесінде қиылысады, ал бүйір қабырғаларының созындылары Ғ нүктесінде қиылысады. ЕҒ түзуі трапеция табандарын қақ бөлетінін дәлелдеңдер (В-3 - сурет).
29. *. Табаны АС, оған қарсы жатқан бұрышы 36° болып, келген тең бүйірлі ABCүшбұрышының AD биссектрисасы жүргізілген. 1) ABCжәне CAD үшбұрыштарының ұқсастығын дәлелдеңдер.
2) ABC үшбұрышының бүйір қабырғасын а - ға тең деп алып, оның табанын табыңдар.
30. ABCжәне А1В1С1 үшбұрыштарының В мен В1 бұрыштары тең. ABCүшбұрышының В бұрышына іргелес қабырғалары А1В1С1 үшбұрышының В1 бұрышына іргелес қабырғаларынан 2,5 есе артық. АС мен А1С1 қосындысы 4,2 м-ге тең деп алып, осы қабырғаларды табыңдар.
Сурет В-3 Сурет В-4
31. С бұрышы сүйір болып келген ABCүшбұрышының АЕ және BDбиіктіктері жүргізілген. Сонда ∆ ABC ∞ ∆ EDC болатынын дәлелдеңдер.
32*. Сүйір бұрышты ABC үшбұрышының AD, BE, СҒ биіктіктері жүргізілген. ABC үшбұрышының бұрыштары белгілі деп алып, DEF үшбұрышының бұрыштарын табыңдар (В-4 - сурет).
33*. 32-есепте айтылған DEFүшбұрышының биссектрисалары ABCүшбұрышының биіктіктерінде жататындығын дәлелдеңдер.
34. Тең қабырғалы екі үшбұрыш ұқсас па?
35. Мына деректерге қарағанда ABC және А1В1С1 үшбұрыштары ұқсас па:
1) АВ = 1 м, АС =1,5 м, ВС = 2 м;
А1В1=10 см, А1С1= 15 см, В1С1= 20 см;
2 ) АВ = 1 м, АС = 2 м, ВС = 1,5 м;
А1В1=8 дм, А1С1= 16 дм, В1С1=12 дм;
3) АВ= 1 м, АС = 2м, ВС= 1,25 м;
А1В1= 10 см, А1С1= 20 см, В1С1 = 13 см?
36. Ұқсас үшбұрыштардың периметрлерінің қатынасы сәйкес қабырғаларының қатынасындай болатынын дәлелдеңдер.
37. Үшбұрыш қабырғалары 0,8 м, 1,6 м және 2 м. Бұған ұқсас үшбұрыштың периметрі 5,5 м-ге тең, осы үшбұрыштың қабырғаларын табыңдар.
38. Бір үшбұрыштың периметрі оған ұқсас үшбұрыш периметрінің 11: 13 бөлігіндей. Сәйкес екі қабырғаның айырмасы 1 м-ге тең. Осы қабырғаларды табыңдар.
39. Тік бұрышты екі үшбұрыштың біреуінің 40° бұрышы бар, ал екіншісінің: 1) 50°-қа тең; 2) 60°-қа тең бұрышы бар, осы үшбұрыштар ұқсас па?
40. Тік бұрышты үшбұрыштың гипотенузасына түсірілген биіктігі гипотенузаны 9 см және 16 см кесінділерге бөледі. Үшбұрыштың қабырғаларын табыңдар.
41. Тік бұрышты үшбұрыштың гипотенузасы 25 см-ге, ал катеттерінің бірі 10 см-ге тең. Екінші катетінің гипотенузадағы проекциясын табыңдар.
42. Ұқсас үшбұрыштардың сәйкес биіктіктерінің қатынасы сәйкес қабырғаларының қатынасындай болатынын дәлелдеңдер.
43. Тік бұрышты үшбұрыш катеттерінің қатынасы т: п қатынасындай. Катеттердің гипотенузаға түсірілген проекцияларының қатынасын табыңдар.
44. Фабрика құбырынан түскен көлеңкенің ұзындығы 35,8 м, жерге тігінен (вертикаль) шаншылған, биіктігі 1,9 м, қаданың сол мезеттегі көлеңкесінің ұзындығы 1,62 м. Құбырдың биіктігін табыңдар (В-5 - сурет).
Сурет В-5 Сурет В-6
45. ABCүшбұрышына ADEFромб іштей сызылған, А бұрышы ортаң та, Е төбесі ВСқабырғасына келіп тірелген (В-6 - сурет). АВ = с және AC = b деп алып, ромб қабырғасын табыңдар,
46. *. ABCүшбұрышының Стөбесіндегі сыртқы бұрышының биссектрисасы АВтүзуін D нүктесінде қияды (В-7 - сурет). Сонда АD:ВD = АС:ВС болатынындәлелдеңдер.
47. *. Берілген екі нүктеге дейінгі ара қашықтықтарының қатынасы тұрақты болып қалатын (бірге тең емес) нүктелерінің геометриялық орны шеңбер болатынын дәлелдеңдер.
48. Үшбұрыштың қабырғасы 10 см-ге тең де, ал оған қарсы жатқан бұрыш 150°. Сырттай сызылған шеңбердің радиусын табыңдар.
49. A, В, С нүктелері шеңбер бойында жатыр. Егер ABC бұрышы 30°-қа, ал шеңбердің диаметрі 10 см-ге тең болса, АСхордасы неге тең болады?
50. A, В, С нүктелері шеңбер бойында жатыр. Егер АСхордасы шеңбердің радиусына тең болса, ABC бұрышы неге тең болады? (Екі жағдайды қарастыру керек.)
51. Тік бұрышты үшбұрышқа сырттай сызылған шеңбердің центрі гипотенузаның ортасы екендігін дәлелдеңдер.
52. Тік бұрышты үшбұрыштың гипотенузасына жүргізілген медиана оны тең бүйірлі екі үшбұрышқа бөлетінін дәлелдеңдер.
53. Гипотенуза мен тік бұрыштың төбесінен сол гипотенузаға түсірілген биіктік бойынша тік бұрышты үшбұрышты салыңдар.
Сурет В-7 Сурет В-8
54. Шеңбер бойынан төрт нүкте A, В, С, D белгіленген. Егер ABC бұрышы а-ға тең болса, ADC бұрышы неге тең болады? (Екі жағдайды қарастырыңдар.)
55. Шеңбердің AD және ВС хордалары өзара қиылысады. ABC бұрышы 50°-қа, ал ACD бұрышы 80°-қа тең. CAD бұрышын табыңдар.
56. *. ІІІеңберге іштей сызылған төртбұрыштың қарама-қарсы жатқан бұрыштарының қосындысы 180°-қа тең екендігін дәлелдеңдер.
57. Қабырғалары берілген екі нүктеден өтетін тік бұрыштардың төбелерінің геометриялық орны шеңбер болатынын дәлелдеңдер.
58. Қабырғалары берілген екі нүкте арқылы өтетін, ал төбелері сол нүктелерді қосатын түзудің бір жағында жататын, мұнымен қоса градустық өлшемі белгілі бұрыштар төбелерінің геометриялық орны, ұштары сол нүктелерде жататын шеңбер доғасы болатынын дәлелдеңдер (В-8 - сурет).
59. Шеңбер хордасымен және шеңберді сол хорданың ұшынан жанап өтетін жанаманың арасындағы бұрыш хорданың ұштарына жүргізілген радиустардың арасындағы бұрыштың жартысына тең болатынын дәлелдеңдер (В-9 - сурет).
60. Бір қабырғасы мен оған қарсы жатқан бұрышы және сол бұрыштың төбесінен жүргізілген биіктігі бойынша үшбұрыш салыңдар.
61. Шеңбердің С нүктесінен оның АВдиаметріне CD перпендикуляры жүргізілген. CD2=AD*BD болатынын дәлелдеңдер.
62. 
Шеңберді қиюшы кесінділердің көбейтіндісі сол нүктеден жүргізілген жанама кесіндісінің квадратына тең болатынын: AC*BC = CD2 дәлелдеңдер (В-10 - сурет).
Сурет В-9 Сурет В-10
Осымша С
