1. АВ бағытталған кесіндісіне гомотетиялы фигура кесінді болады, яғни А1В1 = к АВ. Бұл кесінді берілген кесіндіге параллель және оның ұзындығы к АВ болады.
2.Гомотетия центрі өзіне өзі бейнеленеді
3.Егер к >0 болса, онда гомотетиялы фигуралар О центрінен бір жақта жатады. Егер к <0 болса, онда гомотетиялы фигуралар О центрінің екі жағында жатады.
Салдар. 1) Гомотетияны қолданғанда фигураның барлық өлшемдері к санына пропорционал өзгереді.
1).Гомотетиялы фигуралар ұқсас болады.
2).Егер берілген Ф және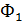 
екі фигураның біріне тең, ал екіншісіне гомотетиялы Ф2 фигурасы болса, онда Ф мен Ф1 фигуралары ұқсас деп аталады.
Мысал. Коэффициенті к болғандағы (N,r) шеңберіне гомотетиялы фигураны салу керек.
Берілгені (N,r) шеңбері, гомотетия коэффициенті к.
Ш е ш у і.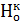 
- гомотетияны қарастыралық. Егер 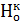(0) = О,
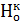= (N) 
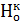және (М) =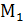 
болса, онда O 
= kON, 
kNM,
O 
= kОМ тендіктері орналады, ендеше 
= kNM, 
болады. Сонымен, w(N,r) шеңбері 
гомотетия арқылы (
шеңберіне бейнеленеді [17].
Гомотетияның мынадай қарапайым қасиеттері бар:
1°. Гомотетия түзуді өзіне параллель түзуге көшіреді, ал гомотетия центрі арқылы өтетін түзуді өзіне - өзін көшіреді.
2°. Гомотетия кесіндіні өзіне параллель кесіндіге көшіреді.
3°. Гомотетия бұрышты өзіне тең бұрышқа көшіреді.
4°. Гомотетия шеңберді шеңберге көшіреді. Жалпы, кез келген екі шеңберді өзара гомотетиялы деп қарастыруға болады. Мұнда ұқсастық коэффициенті олардың радиустарының қатынасына тең.
5°. Егер 
нүктесі ОА сәулесінде жатса, онда центрі О болатын және А- ны А1 нүктесіне бейнелейтін бір ғана гомотетия табылады.
6°. Әрбір ұқсастық түрлендіруін қозғалыс пен гомотетияны бірінен кейін бірін қолдану арқылы алуға болады. Мұнда ұқсастық түрлендіруі мен гомотетияның ұқсастық коэффициенттері бірдей болады.
Мысалы, 2-суретте ABC үшбұрышын А1В1С1 үшбұрышына ұқсастық түрлендіруі қарастырылған. Бұл ұқсастық түрлендіруін алу үшін, алдымен ABC үшбұрышына гомотетиялы А1В1С1 үшбұрышын тұрғызып, сонан соң бұл үшбұрышты А1 төбесінің маңында сағат тілінің бағытымен α бұрышына бұрамыз.
Сурет-2
Келтірілген қасиеттердің алғашқы бесеуі оңай дәлелденеді, ал 6°- қасиеттің дәлелдемесі мектеп бағдарламасына енбегендіктен, оны дәлелдеу қажет емес.
Ескерту. Гомотетияның анықтамасы бойынша А және А1 нүктелері ОА сәулесінде жатады деп айтылған. Енді А1 нүктесін ОА сәулесінің толықтауыш ОА сәулесін алып, 
= к шарты орындалсын делік (3-сурет). Бұл түрлендіруді кері немесе теріс гомотетия деп те атайды. Ал біз бұл түрлендіруді гомотетияға қоспай, жай ұқсастық түрлендіруі ретінде қарастырамыз. Өйткені, әуелі ABC үшбұрышын (3-суреттегі) онымен гомотетиялы А2В2С2 үшбұрышына көшіріп, сонан соң бұл үшбұрышқа центрлік симметрияны қолданып, А1В1С1 үшбұрышын аламыз [7].
Сурет-3
