Шеңбер
Шеңбер деп берілген нүктеден бірдей қашықтықта жатқан жазықтықтың барлық нүктелерінен тұратын фигураны айтады. Берілген нүкте шеңбердің центрі деп аталады.
ПІеңбер нүктелерінен оның центріне дейінгі ара қашықтық шеңбердің радиусы деп аталады. Радиус деп, сондай-ақ шеңбер нүктесін оның центрімен қосатын кез келген кесіндіні айтады (24-сурет).
Шеңбердің екі нүктесін қосатын кесінді хорда деп аталады. Центр арқылы өтетін хорда диаметр деп аталады. 25-суреттегі ВС — хорда, AD— диаметр.

Сурет24 Сурет25 Сурет26
Есеп (6). Хорданың ортасы арқылы өтетін диаметр хордаға перпендикуляр болатынын дәлелдеңдер.
Шешуі. АВ — шеңбердің хордасы, ал С— оның ортасы болсын (26-сурет). АОВ— табаны АВболатын тең бүйірлі үшбұрыш. Оның ОА және ОВқабырғалары шеңбердің радиустары болғандықтан тең. Тең бүйірлі үшбұрыш -тың табанына жүргізілген медианасының қасиеті бойынша ОС кесіндісі биіктік болып табылады. Сондықтан хорданың ортасы арқылы өтетін диаметр хордаға перпендикуляр болады
Үшбұрышқа сырттай сызылған шеңбер
Егер шеңбер үшбұрыштың барлық төбелері арқылы өтсе, онда ол үшбұрышқа сырттай сызылған шеңбер деп аталады.
Теорема 6. Үшбұрышқа сырттай сызылған шеңбердің центрі үшбұрыш қабырғаларының орталары арқылы жүргізілген перпендикулярдың қиылысу нүктесі болып табылады.
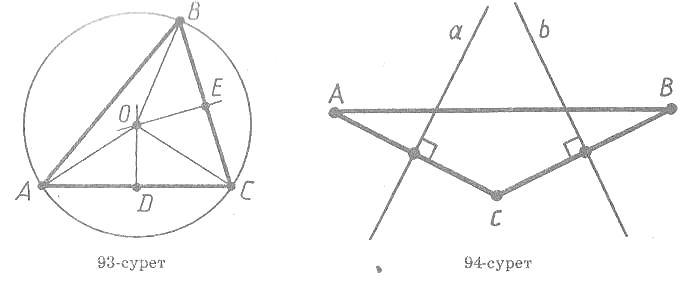
Сурет27 Сурет28
Дәлелдеу. Айталық ABC — берілген үшбұрыш және О — оған сырттай сызылған шеңбердің центрі болсын (27-сурет). АОС үшбұрышы тең бүйірлі: оның ОАмен ОСқабырғалары радиустар болғандықтан тең. Бұл үшбұрыштың OD медианасы оның биіктігі де болып табылады. Сондықтан шеңбердің центрі АСқабырғасына перпендикуляр әрі оның ортасынан өтетін түзудің бойында жатады. Дәл осылайша шеңбердің центрі үшбұрыштың қалған екі қабырғасының да перпендикулярында жататыны дәлелденеді. Теорема дәлелденді [27].
Ескерту. Кесіндінің ортасы арқылы өтіп және оған перпендикуляр болатын түзуді көбінесе орта перпендикуляр деп атайды. Осыған байланысты кейде былай дейді: үшбұрышқа сырттай сызылған шеңбердің центрі үшбұрыш қабырғаларының орта перпендикулярының қиылысу нүктесінде жатады.
Есеп (7). Үшбұрыштың екі қабырғасының орта перпендикуляры қиылысатынын дәлелдеңдер.
Ш е ш у і. Айталық, ABC — үшбұрыш, ал а және b — оның АС және ВС қабырғаларының орта перпендикуляры болсын (28-сурет). а жөне b түзулері қиылыспайды, яғни параллель деп жориық. АСтүзуі а түзуіне перпендикуляр. ВСтүзуі b түзуіне перпендикуляр, демек, ол a түзуіне де перпендикуляр, өйткені а және b түзулері параллель. Сонымен АС және ВС түзулерінің екеуі де а түзуіне перпендикуляр, олай болса, олар параллель. Ал бұл дұрыс емес. АС және ВСтүзулері С нүктесінде қиылысады. Біз қайшылыққа келдік. Пікір дәлелденді [27].
Шеңберге жанама
Шеңбердің бір нүктесі арқылы өтіп және осы нүктеге жүргізілген радиусқа перпендикуляр болатын түзу жанама деп аталады. Шеңбердің берілген нүктесі жанасу нүктесі деп аталады.
29-суретте а түзуі шеңбердің Анүктесі арқылы ОА радиусына перпендикуляр болып өтеді. а түзуі шеңберге жанама болып табылады. А нүктесі жанасу нүктесі болып табылады. Былай айтуға да болады: шеңбер а түзуін А нүктесінде жанайды.

Сурет29 Сурет30
Есеп (8). Шеңбер мен жанаманың жанасу нүктесінен басқа ортақ нүктесі жоқ екенін дәлелдеңдер.
Шешуі. a — шеңберге А нүктесінде жүргізілген жанама болсын
(30-сурет). Жанама мен шеңбердің А нүктесінен өзге тағы бір ортақ нүктесі В бар деп жориық. АОВ— табаны АВболатын тең бүйірлі үшбұрыш болады. Оның ОАжәне ОВ қабырғалары — шеңбердің радиустары. Тең бүйірлі үшбұрыштың табанындағы бұрыштары тең, ал Атөбесіндегі бұрышы тік болғандықтан, бұл үшбұрыштың екі тік бұрышы бар болады. Ал, бұл мүмкін емес. Біз қайшылық -қа келдік. Пікір дәлелденді.

Ортақ нүктесі бар екі шеңбердің осы нүктеде ортақ жанамасы бар болса, шеңберлер осы нүктеде жанасады дейді (31- сурет). Егер шеңберлердің
Сурет31
центрлері ортақ жанаманың бір жағында жатса, онда жанасу іштей жанасу деп аталады (31, а - сурет). Егер шеңберлердің центрлері ортақ жанаманың әр жағында жатса, онда жанасу сырттай жанасу деп аталады (31, б-сурет).




