Салуға берілген есептерді ұқсас түрлендіру (гомотетия) әдісімен шығару мысалдары

 

Есеп шығарғанда гомотетия әдісін пайдалануды мынадай ретпен жүргізген тиімді болады.

Есепке анализ жасап, іздеп отырған фигурамыздың өлшемдерін сипаттайтын шарттардың бірін алып тастайды. Мысалы, іздеп отырған үшбұрыштарымыздың қабырғасы жазықтықтың белгілі бір нүктесі арқылы өту керек деген немесе оның кез-келген бір төбесі берілген шеңбердің бойында жатуы тиіс деген шартын алып тастап, алдымен іздеп отырған Ф фигурасын емес, оған гомотетиялы Ф' фигурасын салу мүмкіндігін анықтайды. Сонан соң Ф' фигурасын салып, оны - түрлендіріп болған соң, бұрын тастаған шарт орындалатындай етіп, гомотетиялы түрлендірулер жасайды, сонда іздеп отырған Ф фигура шығады.

Жоғарыда айтылғандардан, гомотетия методымен шығарылатын есептер қатарына ең алдымен берілгендерінің ішінде тек біреуі ғана кесіндімен бейнеленіп, ал қалғандарының не бәрі бұрыштар, не бұрыштардың не кесінділердің қатынастары болып келген есептер жататындығы шығады.

Бұл типтес есептерді шешкенде мыналарды еске алу қажет.

1) Гомотетия центрі ретінде жазықтықтың кез-келген нүктесін алуға болады, ал іс жүзінде гомотетия центрін дұрыс таңдап алу салуды оңайлата түседі. Есепті оңай және тез шешуге келтіретін алдын ала таңдап алу есептің шарты мен талабына байланысты. Гомотетия центрі ретінде көбінесе берілген фигураға көмекші фигураның бір төбесін немесе сызықтық элементінің бір ұшын алатындығын байқауға болады. Мысалы, А төбесіндегі бұрышты және сырттай сызылған шеңбердің R радиусы бойынша тең бүйірлі ВАС үшбұрышын салу үшін ұқсас А төбесіндегі бұрышы мен тең бүйірлі В 'А' С' үшбұрышын салып, сонан соң осы үшбұрышты сырттай сызылған шеңбердің центрін гомотетия ретінде алып және k = R деп жоримыз да В 'А' С' үшбұрышын іздеп отырған үшбұрышқа түрлендіреміз.

2) Ұқсас екі фигураның сәйкес сызықтық элементтерінің қосындысының (айырмасының) қатынасы. Олардың ұқсас (сәйкес) сызықтық элементтерінің қатынасына және гомотетияның k коэффициентіне тең, мысалы, ұқсас үшбұрыштардың периметрлері олардың сәйкес қабырғаларының гомотетия коэффициенті ретінде алынады. Ұқсас екі фигураның аудандары олардың сәйкес элементтерінің квадраттарының қатынасындай болады [30].

Әртүрлі коэффициентті гомотетияға мысалдар қарастырайық.

53 - суретте центрі М₀ нүктеде және коэффициенті k=2 болған гомотетиядағы АВС үшбұрышының бейнесі құрылған, ал екіншіде центрі М₀ нүктеде және коэффициенті k= - 2 болған гомотетия мысалы көрсетілген.

Бұл сызбалардан байқайтынымыз суреттерде жұп ұқсас үшбұрыштар бейнеленген. Екі жағдайда да ұқсастық коэффициенті 2 және де АВС және

А¹В¹С¹үшбұрыштарының сәйкес қабырғалары өзарапараллель.

Сурет - 53.Центрі М₀ нүктеде және Сурет - 54. Центрі М₀ нүктеде және

коэффициенті k=2 болған гомотетия коэффициенті k=-2 болған гомотетия.

Мысал 27. Центрі үшбұрыш медианаларының қиылысу нүктесіндежәне

коэффициенті гомотетиядағы осы үшбұрыштың төбелері қарсы жатқан қабырғаларының ортасына өтеді.

Дәлелдеу. 55-суреттегі сызбаны қарастырайық.Үшбұрыш медианасының белгілі қасиеті бойынша, медианалар қиылысу нүктесі оларды төбеден бастағанда 2:1 қатынасында бөледі.

Сонымен, центрі М нүктеде және коэффициенті болатынгомотетияда, А төбесі А ₁ төбесіне, Втөбесі В₁ төбесіне, ал С төбесі С₁ төбесіне көшеді. Осыны дәлелдеу керек еді.

Сурет 56.28 мысалға.

Сурет -55. 27 мысалға.

Ескерту. АВС және А₁В₁С₁үшбұрыштар гомотетиялы.

Мысал 28. Үшбұрыштың биіктіктері бір нүктеде қиылысады.

Дәлелдеу. А₁В₁С₁үшбұрышын қарастырайық.Оның төбелері арқылы қарама-қарсы қабырғаларынапараллель түзулер жүргізейік. Берілген үшбұрышқа гомотетиялы АВС үшбұрышын аламыз. Бірінші үшбұрыштың төбелері екінші үшбұрыштың қабырғаларының орталары болатынын дәлелдеуді оңай көрсетуге болады (өздерің көрсетіңдер). Берілген үшбұрыштың А₁Н₁, В₁Н₂ и С₁Н₃ төбелеріАВСүшбұрыш қабырғаларының орталарынан өтеді.

Қарастырылып жатқан үшбұрыштардың сәйкес қабырғаларының параллельдігінен, А₁Н₁, В₁Н₂ және С₁Н₃ түзулері АВСүшбұрыштың сәйкес қабырғаларына перпендикуляр болады. Басқаша айтқанда бұл түзулер АВС үшбұрыш қабырғаларының ортасына жүргізілген перпендикулярлар болады. Орталық перпендикулярлар бір нүктеде қиылысатындығы белгілі және оны дәлелдеу қиын емес. А₁Н₁, В₁Н₂ және С₁Н₃ қарастырылып жатқан түзулердің бір нүктеде орталық перпендикулярлар ретінде қиылысатындығынан А₁В₁С₁ үшбұрыштың биіктіктері ретінде де қиылысатындығы келіп шығады. Осыны дәлелдеу керек еді.

Практикада екі гомотетиялы фигураның гомотетия центрін табу білігі үлкен маңызға ие (мысалы олар екі параллель кесінді, сәйкес қабырғалары параллель екі үшбұрыш, екі шеңбер және т.б. болуы мүмкін). Бұндай салуды орындау оңай: сәйкес екі нуктеден түзулер жүргізу керек, осы түзулердің қиылысу нүктесі гомотетия центрі болады. 57-суретте АВ и А₁В₁ кесінділері үшін екі гомотетия центрін салу көрсетілген.

Сурет 57. Екі параллель кесінділер үшін гомотетия центрін салу.

Егерсәйкеснүктелер ретінде А және В₁, В және А₁ нүктелеріналатын болсақ, онда О₁ центрі алынады. Егерсәйкеснүктелер ретінде А және А₁, В және В₁ нүктелеріналатын болсақ, онда О₂ центрі алынады. Екі әртүрлі центрге ие, тең емес шеңберлерде екі гомотетия центрлеріне ие болатындығына оңай көз жеткізуге болады. Осы центрлерді салу мысалдарын қарастырайық.

Мысал 4. Екі шеңбер үшін гомотетия центрін салу.

Салу.

1) Бірінші шеңбер үшін кезкелген О₁А радиусін саламыз. Екінші шеңбердің центрі арқылы О₁А кесіндісіне параллель етіп шеңбердің ВВ’ диаметрін жүргіземіз.

2) Центрлер сызығын құрамыз (О₁О₂ түзуін).

3) АВ және О₁О₂ – лардың қиылысуы О бірінші гомотетия центрін береді.

Сурет 58. Екі шеңбер үшін гомотетия центрін салу.

Ал АВ’ және О₁О₂ - лардың қиылысуы О’ екінші гомотетия центрі болады. Екі шеңбердің гомотетия центрін салу – салудың күрделі есептерін шешуде маңызды басқыш: екі шеңбердің ортақ жанамасын салуда. Бұл салуды орындау үшін бізге бір тұжырымды дәлелдеуге тура келеді.

Тұжырым. Гомотетияда шеңберге жанама шеңберге жанамаға өтеді, сонымен қатар, егер жанама гомотетия центрінен өтсе, онда ол екінші шеңберге де жанама болып табылады.

Дәлелдеу. Айқынфактілерден бастайық. Біріншіден, гомотетия шеңбер радиусын радиусқа көшіреді. Екіншіден, гомотетияда түзулер арасындағы бұрыштар сақталады. Сонымен, егер жанама бірінші шеңбер радиусына перпендикуляр болған болса, онда оның кескіні де екінші шеңбер радиусына перпендикуляр болады. Демек, жанама кескіні де жанама болады. Енді ортақ жанаманың гомотетия центрінен өтетінін көрсетеміз. Жалпы айтқанда, бұл 4 мысалдағы салудан келіп шығады, біз үшін маңыздысы сәйкес гомотетияда радиустардың параллель болатындығы, ал ортақ жанамаға қиылысу нүктесінде жүргізілген радиустардың параллельдігі айқын. Екінші жағынан гомотетия центрінен өтетін түзу өз-өзіне бейнеленеді. Сонымен гомотетия центрінен өтетін бірінші шеңбер жанамасы екінші шеңбер жанамасына және өз-өзіне бейнеленеді, сондықтан ол ортақ жанама болады. Тұжырым дәлелденді [17].

Енді екі шеңберге ортақ жанаманы салу процесін баяндайық.

Мысал 29. Екі шеңберге ортақ жанаманы салу.

Салу.

1 басқыш. Бұлшеңберлер үшін гомотетия центрін құрамыз. (мысал 4-ке қараңыз).

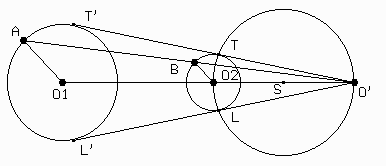Сурет 59. Ортақ жанаманы салу.

2 басқыш. Құрылған гомотетия центрінен шеңберлердің біріне жанама жүргіземіз. Ол екінші шеңберге де жанама болады. Шеңберге жанама салуды ескерте кетейік:

- шеңбер центрін және жанама өтетін нүктені қосатын кесінді ортасын құрамыз (біздің жағдайымызда бұл О’О₂ кесіндісіндегі S нүктесі).

- центрі S нүктесінде, O’нүктеден өтетіншеңбер саламыз.

- Берілген және салынған шеңберлердің қиылысу нүктесін табамыз. (бұл Т и L нүктелер).

- О’Т және О’L түзулерін саламыз– бұлар ізделінді жанамалар болады.

Сурет 60. мысал 30 - ға сызба.

Мысал 30. Шеңбер сегментіне екі шеңбер іштей сызылған (суретке қараңыз). Осы шеңберлердің сегмент доғасымен жанасу нүктесі және шеңберлердің сегмент табанымен жанасу нүктесі арқылы өтетін (АЕ и BF түзулері) түзулер үлкен шеңберде қиылысады. Осы сегментке іштей сызылған кезкелген екі шеңбер үшін қиылысу нүктесі сәйкес келеді.

Шешуі.

Екі гомотетияны қарастырамыз. Центрі А-да болған олардың бірі, центрі О₁ болған шеңберді центрі О- болатын шеңберге бейнелейді. Мұнда MN хорда үлкен шеңбердің С нүктесінен өтетін жанамаға бейнеленеді. Қиылысу нүктесі қиылысу нүктесіне көшетіндіктен, Е нүктесі С нүктесіне бейнеленеді. Демек, А, Е және С нүктелері бір түзуде жатады. Центрі В нүктесінде болатын ұқсас гомотетия центрі О₁ нүктеде болған шеңберді үлкен шеңберге бейнелейді. Мұнда MN хорда үлкен шеңбердің С нүктесінен өтетін жанамаға бейнеленеді. Бірінші гомотетиядағыдай, В, F және C нүктелері бір түзуде жатады.

Сонымен түзулер үлкен шеңбердің С нүктесінде қиылысады [4].

31 - мысал. Екі бұрышы мен периметрі бойынша үшбұрыш салу керек.

Талдау. Есепте екі бұрыш: α,, β және бір кесінді Р берілген. егер үшбұрыш периметрі Р - ға тең болсын деген талапты ескермесек, онда екі бұрышының бірі α,, екіншісі β болатын шексіз көп үшбұрыштар салуға болады.

Іздеген ∆АВС салынған дейік. Мұндағы ∠BAС =α, ∠ACB =β, және АВ+ВС+АС=Р болсын (61-сурет).

АС-дан С₁ нүкте алып СВ-ға параллель C₁В₁ кесіндісін салайық. Сонда ∆АВС~∆АВіСі болады. Сондықтан егер АС₁+C₁В₁+В₁А=Р₁ десек, онда

болады.

Сурет-61

AC түзуінің бойына AD=P кесіндісін өлшеп салып В₁С₁//ВС жүргізсек ∆ABD~∆АВ₁D₁ болады да (**) болады. (*) мен (**) ден AD₁=P₁ болады.

Салу. а) Бір бұрышы ∠B₁AC₁ екінші бұрышы ∠АB₁C₁=β болатын кез-келген ∆ АB₁C₁ саламыз.

б) А нүктеден AC₁ сәулеге АC₁+С₁В₁+В₁А=Р₁ болатын кесінді саламыз. Ол AD₁ болсын.

в) АC₁ сәулеге А нүктеден Р кесіндіні өлшеп саламыз. Ол AD болсын.

г) D₁ В₁ -гe D-дан DB параллель түзуін жүргізіп В нүктесін саламыз.

д) В - дан В₁C₁//ВС жүргізіп С - ны табамыз. ABC іздеген үшбұрыш болады.

Дәлелдеу. ∠BAC = α салу бойынша. Салу бойынша ∠АB₁C₁ = β және В₁C₁//ВС. Сондықтан ∠ ACB=β.

∆АВС-ның периметрін Р₀ десек, онда ∆АB₁C₁~ ∆АВС-дан (*_**), ∆АD₁В₁~∆АDВ-дан = (*_** *) Сонда (*_**) мен (*_** *)- ден

болсын Р₀=Р шығады.

Сонымен ∆АВС-ның периметрі есеп шартында айтылған Р кесіндіге тең екен. Сондықтан ол іздеген үшбұрыш болады.

Зерттеу. ∆АB₁C₁ салыну үшін α+β<180 болуы керек. Көрсетілген салулар бірмәнді орындалатындықтан есептің бір шешімі болады, ал a + β ≥ 180 болғанда есептің шешімі болмайды.

32-мысал. Шыңдарындағы бұрыштары және негіз бен биіктіктің қосындысында теңқабырғалы үшбұрыш салу керек.

Талдама. Ізделініп жатқан үшбұрыш үш шартқа сай келу керек:

1) ол теңқабырғалы болу керек;

2) шыңның бұрышы берілген 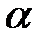бұрышына тең болу керек;

3) негіздің және сай келетін биіктіктің қосындысы 1 кесіндісіне тең болу керек.

Байқауға болады, алғашқы екі шартқа сай келетін үшбұрыш салу оңай. Бұндай үшбұрыштар шексіз көп кездеседі.Біз солардың бірін салып көрелік – үшбұрыш В´А´С(62-сурет), бұл кезде В´А´С= .

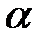Ізделінуші үшбұрыш, шартқа сай болып келеді 1)-3), оны үшбұрыштар арасынан іздейміз, В´А´С үшбұрышына гомотетиялы, бір ұқсастың центріне қатысты, мысалы А нүктесіне қатысты. Мейлі ВАС ізделінуші болсын. Түсінікті, егер ВС||В´С (немесе ВС В´С). Мейлі АР´ – В´А´С үшбұрышының биіктігі, Р – қиысу нүктесі ВС және АР´. Түсінікті, мұнда АР – ВАС үшбұрышының биіктігі.

Егер бір гомотетияда В´ нүктесіне В нүктесі сай келсе, онда С´ және Р´ нүктелеріне С және Р нүктелері сай келеді. В´А´С үшбұрышын ВАС үшбұрышына айналдыратын гомотетияның коофециентін табамыз.шарт бойынша 1 кесінді берілген, ол ВС+АР= l. Сонымен қатар, В´А´С үшбұрышына ие болғаннан соң, біз l´кесіндіні сала аламыз, нәтижесінде В´С´+АР´.

Мұндай іделінуші гомотетия коэфициенті тең болады: , т.е. .

Сонымен, үшбұрыш ВАС В´А´С үшбұрышына гомотетиялы А ұқсастық центріне қатысты, ұқсастық коэфициенті тең: .

Берілген бойынша ізделінуші ВАС үшбұрышын құруға болады.

 

62-сурет

 

Құру.

1) Кез-келген В´А´С үшбұрышын саламыз(62-сурет), шарттарға жауап береді 1) және 2) (сонда В´А=С´А және В´А´С= ).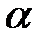

2) Осы үшбұрыштың биіктігін саламыз АР´ және АР´ кесіндісінің бойына P´F´=B´C´ кесіндісін қоямыз, болады AF´=AP´+B´C´. Бұл сумманы l´арқылы белгілейміз.

3) AP´сәулесіне F нүктесін құрамыз, AF= l сияқты..

4) ВАС құрамыз В´АС´ сай келеді Г{A, }гомотетиясында. Бұл үшін ретімен құрамыз FB||F´B´, BC||B´C´. ВАС ізделінуші.

Дәлел. Мейлі Р´ B´C´ АР. Өйткені ВАС және В´АС´ұқсастар,сонда

 

.

 

Сондықтан , бірақ АР´+В´С´=l´ құрылуы бойынша. Демек, АР+ВС= l.

Сонда ВАС 3)шартты қанағаттандырады. Демек, 1) және 2) шарттарға да сай келеді деген сөз.

Зерттеу. Құрылған құрылғының барлыққадамдары орындауға боларлықтай. Сондықтан бұл әдіс бойынша бір ғана шешім болады. Кез-келген А₁В₁С₁ үшбұрышы, есеп шартына орай, салынған АВС үшбұрышына ұқсас болып келеді. Сондықтан, А₁В₁С₁, басқа жолмен алынса мына қатынастар орындалады:

.

Өйткені АР´+В´С´=АР+ВС, то и В₁С₁=ВС, бұдан түсінікті А₁В₁С₁= АВС. Сондықтан кез –келген құру амалы осындай бір мәнді шешімге әкеліп соғады.

33-есеп. Үшбұрыштың төбесіндегі бұрышы және табанымен сол табанға жүргізілген биіктігінің қосындысы берілген.

Сол шартты қанағаттандыратын тең бүйірлі үшбұрышты салу керек.

Талдау. Есепте үш шарт берілген: 1 - төбедегі бұрышы болсын, 2- бүйір қабырғалары тең болу керек. 3 - табаны мен биіктігінің қосындысы m - кесіндіге тең болуы керек.

Алғашқы екі шартты қанағаттандыратын шексіз көп үшбұрыш болады. Соның бірі ∆А₁В₁С₁ болсын дейік, (63-а сурет) онда ∆А₁В₁С₁ =α және А₁В=С₁В.

Берілген үш шартты да қанағаттандыратын үшбұрышты центрі В нүкте болатын ∆ ВА₁С₁-ға гомотетиялы болатын үшбұрыштар ішінен іздейміз.

∆ВАС ізделінетін үшбұрыш болсын. Онда АС||А₁С_1, BD биіктік болады. Осы гомотетияда А₁ нүкте А нүктеге сәйкестенсе, онда D₁ нүкте D_1, C₁ нүкте С нүктеге сәйкестенеді.

Осы ∆А₁ВС₁ үшбұрышты ∆АВС- үшбұрышқа сәйкестендіріп гомотетия коэфиценті к - ны табайық. Шарт бойынша BD+AC=m

∆А₁ВС₁ - ны өзіміз салғандықтан BD₁+A₁C₁=m₁ таба аламыз.

Сонда коэффициент К= болады.

Осыны ескеріп ∆ A₁BC₁ арқылы ∆АВС-ны салуға болады (63-сурет).

Салу. а) Кез келген В нүктеден 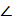В=а болатын бұрыш саламыз.

б) Оның қабырғаларынан BA₁=BC₁ болатын А_1,С₁ нүктелерді саламыз да A₁С₁ кесіндісін саламыз.

в) А₁С₁-ға етіп BD₁ сәулесін жүргіземіз. Оның бойына D₁E₁=A₁C₁ кесінді саламыз. Сонда BE₁=BD₁+A₁C₁=BD₁+D_lЕ₁ m болсын.

г) BE₁ сәулеге ВЕ₂=m кесіндіні өлшеп саламыз.

д) Е₂ -ден E₁A₁-ге параллель жүргізіп, оның ВА мен қиылысу нүктесі А- ны табамыз.

е) А нүктеден А₁С₁-ге параллель етіп АС-ны жүргіземіз. Сонда ABC іздеген үшбұрыш болады.

Сурет-63

Дәлелдеу. Салу бойынша В бұрышы берілген а бұрышына тең BD₁ A₁C_1, АС|| A₁C₁ - болғандықтан BD AC. Сондықтан BD биіктік.

Ал_, ∆АСВ~ ∆А₁В₁С₁, болғандықтан

Демек BD+AС m.

Сөйтіп ∆АВС берілген үш шартты да қанағаттандырады. Сондықтан іздеген фигура болады.

Зерттеу. Барлық салулар бірмәнді орындалады. Сондықтан есептің тек бір шешімі болады.

34-есеп. Табанындағы екі бұрышы және Р периметрі бойынша үшбұрыш салу керек.

Талдау. Есеп шешілген, іздеген ∆АВС салынған болсын (64- сурет). Онда 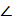BAC =α, 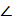BCA =β және АВ+ ВС+ СА=Р берілген периметр. Егер АВ-ны А нүктеден, ВС-ны, В нүктеден бұрып АС жатқан түзуге көшірсек, A₁C₁ A₁A+AC+CC₁ AB +АС+ВС=Р болар еді және АА₁В, С₁СВ үшбұрыштар тең бүйірлі болғандықтан AA₁B= С₁СВ= болады.

Бұлар ∆ABC үшбұрышын салуға мүмкіндік береді.

Салу. а) А_іС_і=Р кесіндіні өлшеп саламыз.

б) А₁ нүктеден А₁С₁ мен а бұрыш, С₁ нүктеден f бұрыш жасайтын түзулер жүргізіп олардың қиылысу нүктесі В-ны табамыз.

в) А,В-ның қақ ортасы А₀ мен С, В-ның қақ ортасы С₀-ды табамыз.

г) А_о-дан А₁В-ға, С₀-дан С₁|В-ға перпендикуляр жүргізіп олардың АС түзумен қиылысу нүктелері А мен С-ны табамыз. Сонда ∆АВС іздеген үшбұрыш болады.

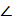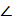Дәлелдеу. А₁В-ның қақ ортасынан оған А₀А перпендикуляр етіп жүргізілгендіктен А₁А=АВ болады. Дәл осы сияқты СВ=СС₁ болады. Соңдықтан А₁А+АС+СС₁=АВ+АС+СВ=Р болады. Үшбұрыштыңсыртқы бұрышының қасиеті бойынша BCA = ВСА = + .

Демек 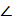ABC іздеген үшбұрыш болады.

Сурет-64 Сурет-65

Зерттеу. <180 болғанда ғана есептің шешуі болады және шешім біреу-ақ болады. Өйткені б-салуда А₁В, C₁D түзулерді А₁С₁ дің екінші жағынан өлшеп салуға болады. Бірақ нәтижеде шығатын үшбұрыштар тең болады.

35-есеп. ABC үшбұрыштар іштей, сүйір бұрышы болатын екі төбесі үшбұрыш табаны АС-дан жататын, қалған төбелері бүйір қабырғаларда жататын ромбы салу керек ( 65-сурет).

Шешуі. Ромбының екі төбесі АС- да жататындықтан оның қарсы қабырғасы АС-ға параллель болады. Сондықтан салуды былайша жүргіземіз.

а) АВ - дан Ғ₁ нүкте алып, ол нүктеден АС- ға параллель түзу және ол түзу мен бұрыш жасайтын Ғ₁Е₁ түзуін жүргіземіз. Параллель түзуге F₁K₁=F₁E₁ саламыз. К₁-ген F₁E₁- ге параллель жүргізіп N- ді саламыз. Сонда F₁K₁F₁E₁ бір сүйір бұрышы _а, екі төбесі АС- да жататын ромбы болады.

б) АК₁ ВС=К нүктені салып, КҒ||К₁Ғ₁ KN||K₁N₁, ЕҒ||Е₁Ғ₁ жүргіземіз. Сонда КҒ||К₁Ғ₁ KN||K₁N₁ болғандықтан EFKN іздеген ромбы болады.

Дәлелі. б КҒ||К₁Ғ₁ KN||K₁N₁ болғандықтан ∆АҒК~ ∆АҒ₁К_1, ∆AKN, ∆AK₁N_i.

Сондықтан 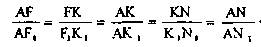. Бұдан E₁F₁F₁K₁K₁N₁,

болғандықтан EF=FK=KN=EN және сәйкес қабырғалары параллель болғандықтан 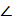EFK= 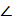E₁F₁K₁= . Сондықтан EFKN іздеген ромбы болады. Есептің әруақытта шешуі болады және ол жалғыз-ақ болады. Өйткені салулар бірмәнді анықталады.

Көріп отырғанымыздай, ұқсас түрлендіру әдісімен жұмыс істегенде гомотетияның негізгі қасиеттерін оқып үйренуге және салу есептерін шығарғанда гомотетияны қолдануға ерекше назар аударуды ұсынамыз. Конструктивті есептерді ұқсас түрлендіру (гомотетия) әдісімен шығаруға кіріспей тұрып, гомотетиялы фигураларды салуды үйрену керек [30].

Гомотетиялы фигураларды салуға мысал

1. Гомотетия S центрі және сәйкес А мен А' қос нүктемен берілген

(66-сурет). Берілген М нүктесіне гомотетиялы нүкте салу керек.

Шешуі. Мына салуларды ретпен орындайық:

1 ) МА түзуін,

2) SM түзуін,

3) 1||MA, A'Сl;

4) I мен SМ түзулерінің қиылысу М' нүктесін белгілейміз, яғни М' = l∩SM. М'— іздеп отырған нүктеміз.

Сурет-66

36-есеп. Диагональдарының m:n қатынасымен һ биіктігі бойынша ромбы салыңдар.

Шешуі: Анализ ABCD ромбысы салынады делік. AC: BD = m: n және EF =һ. Ромбының қасиеті бойынша 1) AO: OD = m: n 2) <AOD =90° және OF = — екендігін байқаймыз. 1) және 2) шарттар бойынша AOD үшбұрышына гомотетиялы A'O'D' үшбұрышын саламыз. О нүктесін гомотетия центрі, ал (һ:һ') қатынасын гомотетия коэффициенті етіп алып, AOD үшбұрышын,содан соң іздер ромбымызды саламыз.

Салу. Алдыңғы екі шарт бойынша іздеп отырған үшбұрышымызға ұқсас А'О'D' үшбұрышын және іздеп отырған AOD үшбұрышымыздың биіктігіне сәйкес келетін оның О ’F’ = биіктігін саламыз. О төбесін гомотетия центрі етіп алып, коэффициент k = = һ:Һ’ деп алайық.

Белгіленген гомотетияда А'О'D' үшбұрышын іздеп отырған AOD үшбұрышына түрлендірейік. Ол үшін О'Ғ' сәулесінің бойына О'Ғ' кесіндісін салып, Ғ нүктесі арқылы A'D'- қа параллель түзу жүргізсек, AOD үшбұрышы шығады, AOD үшбұрышын ромбыға дейін толықтырып саламыз, ол үшін ОС = ОА, ОВ = ОD саламыз да, А мен В-ні, В мен С-ні және С мен D -ні түзу кесінділерімен қосамыз. ABCD- іздеп отырған ромбымыз.

Зерттеу: есептің шартын қанағаттандыратын кез-келген басқа бір А₁В₁С₁D₁ ромбысын салынған ромбыға ұқсас және қатысы орындалуы тиіс болғандықтан, есептің бір ғана шешімі болады. Алайда h₁ =һ, A₁D₁ = AD болады, олай болса, А₁ В₁ C₁D₁ ромбысы ABCD ромбысына тең. Демек есеп бір мәнді шешіледі.

сурет-67

37-есеп. А мен В бұрыштары және үшінші төбесі арқылы өтетін биіктігі мен осы үшбұрышты іштей сызылған шеңбердің радиусының 1 - қосындысы бойынша үшбұрыш салу керек.

Шешуі: Анализ. Егер есептің үшінші шартын ескермесек. Онда А мен В екі бұрышы бойынша іздеп отырған үшбұрышымызға ұқсас шексіз көп үшбұрыш салуға болады. Олардың бірі А'В'С' үшбұрышы болсын. Олай болса, іздеп отырған ABC үшбұрышымызды гомотетия коэффициенті k = болатын S центіріне қатысты A'B'С' үшбұрышына гомотетиялы үшбұрыштар арасынан іздеу керек. (Мұндағы 1’ дегеніміз Һ’с' биіктігін мен А'В'С' үшбұрышына іштей сызылған шеңбердің r' радиусының қосындысы).

Салу: Берілген А мен В бұрыштары бойынша көмекші А'В'С' үшбұрышын саламыз. С'Е' = Һ’с' биіктігін созындысына Е'К' =r', 1’ = СꞌЕ' +Е'К' кесінділерін салайық, С' төбесін гомотетия центрі ретінде алайық және гомотетия коэффициенті k = 1/1ꞌ болсын.

Берілген гомотетияда А'В'С' үшбұрышын іздеп отырған үшбұрышқа түрлендірелік, ол үшін С'К' сәулесінің бойына С'К ꞊ 1 болатындай етіп, К нүктесін салайық. К нүктесі арқылы А' К' || АК түзуін, ал А нүктесі арқылы А'Вꞌ||АВ түзуін

сурет- 68 жүргіземіз. AВС - іздеп отырған үшбұрышымыз.

Дәлелдеу: Е= АВ∙СꞌЕ' болсын ∆АО D∞∆ A¹О¹ D¹ болғандықтан,

Сондықтан

Бірақ салу бойынша С'E'+ОF' = 1 . Олай болса C'Еꞌ+OF =1 және

C'Е+OF =1. ABC үшбұрышы есептің барлық шартын қанағаттандырады.

Зерттеу: Егер А+В<180⁰ болса, онда барлық салулар бір мәнді орындалады. Есептің шартын қанағаттандыратын кез-келген A₁B₁C₁ үшбұрышы салынған үшбұрышқа ұқсас болуы керек, олай болса қатысы орындалуы тиіс. Алайда C'Еꞌ+O F = CЕ+OF =1 болғандықтан, болады. Сондықтан ∆А'В'С'=∆ABC. Сонымен, салуды кезкелген басқа тәсілмен орындағанда да осы шешім шығады. Есептің шешуі бірмәнді орындалады.

38-есеп. А және В төбелері сегменттің табанында, ал D және С төбелері оның доғасында жататын етіп, берілген дөңгелек сегментке ABCD квадратын салу керек.

Шешуі: Анализ. ABCD іздеп отырған квадрат делік. Сегменттің табанына қарағанда онымен бір жақта және төбелері сегмент табанының бойында жатып, F ортасына қарағанда симметриялы болатын көмекші A'B'C'D' квадратын алайық. Сонда центрі F және коэффициенті k= A'B'C'D' квадратын іздеп отырған ABCD квадратына түрлендіреді.

Салу. Сегменттің табанының ортасы –F нүктесін, сонан соң FA' = ҒВ'

Сурет-69

кесінділерін салайық. Сегменттің табанына қарағанда онымен бір жақта жататын және қабырғалары А'В' - қа тең квадрат саламыз. Центрі F нүктесінде коэффициенті к гомотетияның көмегімен салынған A 'B'C'D' квадраты шығады.

Дәлелдеу: Гомотетия қасиеті бойынша ABCD - іздеп отырған квадрат. Есеп шартын толық қанағаттандырады.

Зерттеу: Егер сегменттің доғасы шеңбердің бөлігінен үлкен болмаса, онда есептің бір ғана шешімі болады, ал егер де үлкен болса, онда есептің шешімі болмайды [32].

39-Есеп. Берілген дөңес ABCD төртбұрышына іштей, қабырғалары сол төртбұрыштың диагоналдарына параллель болатын етіп, ромбы салу керек.

Шешуі: Анализ PQMN іздеп отырған ромбымыз делік. A нүктесін гомотетия центрі етіп алып және кез-келген нақты к ≠ 0 салып (мысалы, 0<к<1) гомотетия коэффиценті ретінде алайық. Белгіленген гомотетияда MQPN ромбысы, P'Q'M'N' ромбысына ауысады, ал бұл ромбының қабырғалары да берілген төртбұрыштың диагоналдарына параллель, Р' пен N' төбелері бұл төртбұрыштың қабырғаларында жатпайды, яғни есептің шарттарының екеуі де орындалмайды. Сонымен есеп гомотетияда (центрі А нүктесінде және коэффициенті кꞌ꞊ 1: к = AN:AN') іздеп отырған ромбымызға ауысатын P'Q'M'N' ромбысын салуға келіп тіреледі.

Салу: 1) Q' — АВ - ның бойындағы кез-келген нүкте.

2) Qꞌ М' // BD;

3) M'N' // АС. М' Nꞌ ꞊ М' Q', P'Q'M'N' ромбысын саламыз.

4) AN , N=AN ∩ DC

5) MN // N’M',M Q // М’ Q', QР //АС, РN //QM. PQMN ромбысы-іздеп отырғанымыз.

Дәлелдеу: Р төбесі ВС-нің бойында жатпайды делік. Сонда ромбы болмайтын MQP₁N төрт бұрышын қарастырамыз, мұндағы Р₁= ВС ∩ QР және Р мен Р₁ беттеспейді.

Бұлай болмайтындығын дәлелдейік. Q Р₁ //АС, QМ // BD, M'N' //AC және

Q'M'// BD болғандықтан,

Бұдан P₁Q' = MN және / / MN, яғни P₁QMN - параллелограмм. Ал MNQ және M'N'Q' сынық сызықтары гомотетиялы, олай болса, MN=MQ.

Сонымен P₁QMN - ромбы олай болса, Р₁=Р және PQMN - іздеп отырған ромбымыз.

Зерттеу: Есептің әрқашан да бір ғана шешімі болады. Шындығында, егер төрт бұрышты іштей қабырғалары басқа. Екінші бір ромбы сызылған деп жорысақ, онда PQ үлкейеді (кішірейеді) ал онда QM кішірейеді (үлкейеді), олай болса PQ мен QM тең болмайды, ал ромбыда бұлай болуы мүмкін емес [32].

Сурет-70

40-есеп. Берілген < А бұрышы және һ_а биіктігі d: с қатысы бойынша үшбұрыш салу керек.

Шешуі: Анализ. d: с қатысының ұзындығын белгілі кесінді қатысына тең, яғни m: п деп алайық. Ізделінді үшбұрышқа ұқсас үшбұрыш саламыз.

Ол үшін А бұрышының қабырғаларына сәйкес АС' және АВ' кесінділерін саламыз.

Салу: Ең алдымен ABC үшбұрышына ұқсас АВ'С үшбұрышын саламыз. А төбесін гомотетия центрі ретінде қарастырайық. АВ'= п, ҒСꞌ ꞊ т бұрыш қабырғаларына салып, A'B'Cꞌ үшбұрышын шығарып аламыз. A'B'C' үшбұрышын түрлендіріп ABC үшбұрышын шығарып аламыз.

Дәлелдеме: ∆АВ'С∞∆АВС ұқсас болады.

A — гомотетия центрі. ВꞌС'| |ВС. АD'- үшбұрыш биіктігі, AD = һ_а үшбұрыш биіктігі. АО = һ_а АС:АВ=АС:АВꞌ ꞊ m:n яғни ABC үшбұрышы есеп

шартын толық қанағаттандырады

 

Сурет-71

41-мысал. Тікбұрышты үшбұрыштың катеттеріне жүргізілген медианалары см және см. Оның гипотенузасын табу керек ( 72-сурет ).

72-сурет

Шешуі. ВС мен AC катеттерін сәйкес х пен у арқылы белгілейік. ВСЕ, ACF — тікбұрышты үшбұрыштар болғандықтан, ВС² = BE² - EC² және

CF² = AF² - AC², яғни және . Бұл теңдеулер жүйесін

шешіп, х пен у-ті табамыз:

73 - 0,25y² = 4 • 52 - 4y², y² = 36;
y = 6см, х = 8см; .

42-мысал. ABC үшбұрышында АВ=26см, ВС=30см, АС=28см. В төбесінен ВН биіктігі мен BD биссектрисасы жүргізілген. BHD үшбұрышының ауданын табу керек.

Шешуі. ABC үшбұрышының ауданын екі әдіспен өрнектейік: S^,_c = 0,5АС ■ ВН = 0,5 • 28 • Һ = 14Һ; екінші жағынан .

Демек, 14h = 336, h = 24 см. Енді CD = x деп алып, ABC үшбұрышының ішкі бұрышы биссектрисасының қасиетін пайдаланайық: BC:AB=CD:DA,

30:26=x:(28-x), x=CD=15cm; AD=28-15=13cm. АВСН: СН² = ВС² -ВН² = 324, CH=18 см, DH=CH-CD=18-15=3cm, S=0,5 DH* ВН = 36см².

43-мысал. Медианалары болатын үшбұрыштың ауданын есептеу керек (73-сурет).

Шешуі. AABC: m_b = BE = 9см, m_a = AD = 12см. m_c = CF = 15см. Берілген

элементтер мен іздеген элементтің арасындағы байланысты анықтайық.

(О — медианалардың қиылысу нүктесі).

73- сурет

ОЕ медианасын екі еселеп, АОС үшбұрышын AOCB параллелограмына дейін толықтырайық. Сонда AC² + OB² = 2(AO² + OC²);

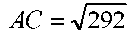. Осы сияқты OD медиананы екі еселеп, ВОС үшбұрышын параллелограмға толықтырсақ:

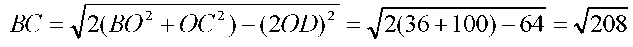
Осылай қарастырып, АВ=10см екенін аламыз. Енді Герон формуласымен ауданды есептесек, .

Осы есепті басқа әдіспен шешейік. ∆ AOC мен ∆ ABC - ның табандары тең

болғандықтан, 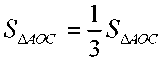Шынында да, болғандықтан, . Сондықтан

Енді AOCB параллелограмынан:

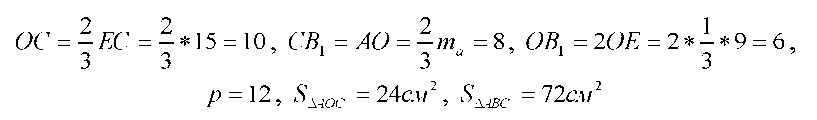
44 - мысал. Тең бүйірлі ABC үшбұрышының табаны AC, төбесіндегі В бұрышы сүйір, С бұрышының биссектрисасы CD кесіндісі болсын. D нүктесі арқылы CD биссектрисасына перпендикуляр түзу жүргізілген. Бұл түзу үшбұрыштың AC табанымен немесе оның созындысымен Е нүктесінде қиылысады. AD =0,5ЕС болатынын дәлелдеу керек (74-сурет).

Есеп геометриялық әдіспен тікелей шешіледі. CD кесіндісі — EFC үшбұрышының әрі биіктігі, әрі биссектрисасы. D нүктесін ВС қабырғасымен

( және CD — С бұрышының биссектрисасы) қиылысқанша созсақ, EFC тең бүйірлі үшбұрышы шығады. Есептің шарты бойынша 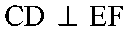. Ендеше ED = DF. D нүктесінен ВС - ға параллель түзу жүргізсек, ол AC табанымен К нүктесінде қиылысады. Бұл DK кесіндісі EDC үшбұрышының медианасы бола алады. ЕК:КС = ED:DF = 1, бұлардан DK = 0,5ЕС, сондықтан AD = DK= 0,5 EC.

74-сурет

45- мысал. Тең бүйірлі трапецияға іштей дөңгелек сызылған. Трапеция

ауданының дөңгелек ауданына қатынасы -ге тең. Трапецияның үлкен

табанындағы сүйір бұрышын табу керек (75-сурет).

ABCD — тең бүйірлі трапециясы берілген, .

Бірінші тәсіл. Есептің мазмұнынан оны синтез әдісімен немесе алгебралық әдіспен шешуге болатынын байқаймыз. Синтез әдісі бойынша берілгендерге сүйеніп дөңгелектің радиусын табуға болады. Дөңгелектің радиусын г, трапецияның табан қабырғалары ұзындықтарын a, b деп қосымша белгісіздер ендіреміз. Есеп шарты бойынша

Екінші жағынан шеңберді сырттай сызылған төртбұрыштың қасиеті бойынша AD+BC=AB+DC теңдігін жаза аламыз. Бұдан 2AD=a+b,

AD=0,5(a+b). Тікбұрышты AED үшбұрышынан ; бұл

теңдікке r-дің мәнін қойып ықшамдасақ, sin A = 0,5 шығады. Сонымен,

75- сурет

Бұл есепте жоғарыда айтылған тірек элементін және қосымша белгісіздер енгізу, теңдеу құру, қосымша белгісіздерді ығыстыру процестерінің барлығы орындалады.

Екінші тәсіл. 75-суреттен AD=BC теңдігін ескеріп, бір нүктеден шеңберге жүргізілген екі жанама тең болатынын пайдалансақ,

r-дің 1-тәсілдегі мәнін орнына қойсақ, sinA = 0,5, бұдан .

Теңдеулер құру арқылы шешілетін есептерді қарастырайық.

46-мысал. Тікбұрышты үшбұрыштың гипотенузасы с-ға тең, үшбұрыштың бір сүйір бұрышынан катеттерінің біріне ұзындығы m-ге тең медиана жүргізілген. Осы үшбұрыш катеттерінің ұзындықтарын табу керек (76-сурет).

76-сурет

Есепті теңдеу құру әдісімен (алгебралық әдіспен) шешу үшін АС=х, BC=y деп белгілейік. Тікбұрышты үшбұрыштардан Пифагор теоремасы бойынша: АС² + ВС² = AB², АС² + CD² = AD² немесе х² + y² = c², х² + (0,5y)² = m².

Бұл жүйенің шешімі .

Математикалық есептердің көбінде қосымша белгісіздер енгізу әдісі қолданылады. Бұл есептердің берілген элементтері мен қажетті теориялық материалдарды байланыстыруға септігін тигізеді. Есепті шешу барысында осы қосымша белгісіздер ығысады.

47-мысал. Ромб биіктігі оның қабырғасын m және n бөліктерге бөледі. Ромб диагоналдарының ұзындықтарын табу керек (77-сурет).

1- тәсіл. Теңдеулер құруға қажетті белгісіздер енгізелік. Ол үшін АС=х,

BD=y деп белгілейміз. Сонда АВ = AE + EB = m + n. Бұл қосымша элементті есеп шартындағы белгілі және белгісіз шамалар арқылы өрнектейміз. ED = h десек, h² = y² - n² және h² = (m + n)² -m². h²-тың мәндерін теңестірсек,

 

77-сурет

у² -n² = (m + n)² -m², y² = 2mn + 2n² немесе . АОВ үшбұрышынан х-ті табамыз:

 

 

Сонда жауабы:

2- тәсіл. Аудандарды пайдалану әдісі бойынша 0,5d₁d₂ шамасын қосымша элементтер арқылы табылатын ауданға теңестіреміз, яғни , мүндағы . АОВ үшбұрышынан

(0,5d)² + (0,5d₂)² = (m + n)² немесе d² + d₂ = 4(m + n)². Бірінші теңдіктің екі жағында 4-ке көбейтіп екінші теңдікке қоссақ, онда

Бірінші теңдіктен d - ді тапсақ және оны соңғы теңдікке қойсақ, түрлендіргеннен кейін болады. Енді

теңдігіне d₂ -нің табылған мәнін қойсақ, екені шығады.

Егер берілген есепте кейбір шамалардың (ұзындықтардың немесе аудандардың) қатынастарын табу қажет болса, дербес жағдайда белгілі бір бұрышты есептеу қажет болса, ондай есептер көмекші параметр енгізу деп аталатын тәсілмен шешіледі. Бүл тәсіл бойынша есепті шешу үшін сызықтық элементтердің біреуін белгілі деп алып, іздеп отырған шаманы сол арқылы өрнектейді де олардың қатынастарын құрады [30].