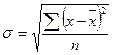Тема 6. Статистична характеристика результатів спостереження

Головне завдання даної теми — ознайомити студентів з основ­ними характеристиками статистичної сукупності поданої у формі ряду розподілу. Залежно від статистичної природи варіант ряди розподілу поді­ляються на атрибутивні та варіаційні. Частотними характеристика­ми будь-якого ряду є абсолютна чисельність j -ї групи - частота f_j та відносна частота j -ї групи - частка d_j. Очевидно, що , а 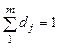, або 100 %.

Базою аналізу закономірностей розподілу слугує варіаційний ряд розподілу —дискретний або інтервальний — з рівними інтервалами.

Типовий рівень ознаки, узагальнююча характеристика її індивідуальних значень характеризується середньою величиною 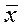. Середня величина є узагальнюючою мірою варіюючої ознаки у статистичній сукупності. Показник у формі середньої характеризує рівень ознаки в розрахунку на одиницю сукупності. Середня характеризуватиме типовий рівень лише за умови, що сукупність якісно однорідна.

Чисельник формули середньої являє собою обсяг значень варіюючої ознаки (визначальну властивість), а знаменник - обсяг сукупності.

Для не згрупованих даних розрахунок середньої здійснюється за відомою формулою:

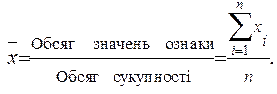
Для згрупованих (групувальні таблиці, ряди розподілу) даних розрахунок середньої здійснюється за наступними правилами:

1)визначається одиниця виміру майбутньої середньої; виходячи з того, що середня є відносною величиною, що має чисельник та знаменник, її одиницею виміру завжди є дріб;

2)значення показника, одиниця виміру якого знаходиться у знаменнику одиниці виміру середньої, записується до знаменника формули розрахунку середньої (п);

3)знаючи, після виконання попереднього етапу, величину знаменника, в чисельнику додається стільки значень ознаки х_і, щоб їх кількість дорівнювала п.

В інтервальних рядах, припускаючи рівномірний розподіл елементів сукупності в межах j -го інтервалу, як варіанту використовують середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою самою, як сусіднього закритого інтервалу.

Для окремих випадків аналізу динаміки використовуються специфічні середні, використання яких буде пояснено у відповідному розділі.

Тобто, середня – розрахунковий узагальнюючий показник, який дозволяє охарактеризувати рівень певної ознаки, притаманної одиницям сукупності, що дозволяє проводити порівняння між собою сукупностей, які містять по декількі елементів (сукупності злочинців, злочинів, співробітників правоохоронних органів, судових справ і т.і).

Слід брати до уваги, що будь-якій сукупності притаманна власна структура. Тому при порівняннях відмінності між середніми можуть бути обумовлені як відмінностями рівнів ознаки у елементів порівнювальних сукупностей (вік засуджених, термін ув’язнення, вартість заподіяних збитків), так і відмінностями в структурах цих сукупностей (співвідношення засуджених різного віку, співвідношення справ по яких визначений різний термін ув’язнення, співвідношення вироків по справах з різною сумою заподіяних збитків). Вплив структури сукупності на рівень середньої походить з природи речей, тобто існує незалежно від бажання чи небажання особи, яка обчислює середню. Тому вміння виділяти вплив зміни структури на характеристику явища, яке досліджується є об’єктивною вимогою до аналізу результатів діяльності правоохоронних органів (детальніше див. тему 8).

Складність розробки заходів по скороченню злочинності та правопорушень позв’язано з кількістю причин (мотивів), що обумовили скоєння злочинів: набагато легше позбутися, шляхом реалізації певних заходів, однієї-двох причин, ніж цілої їх низки. В разі дії на території багатьох чинників злочинів ризик неефективності правових заходів набагато зростає. Для визначення рівня ризику (непевностість результатів діяльності) використовують показники варіації:

а) абсолютні в) відносні (коефіцієнти варіації)

середнє лінійне відхилення лінійний

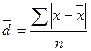
- середнє квадратичне відхилення квадратичний