Кернеу-деформация күйлерінің жеке сұлбалаы

Сызықтық кернеу күйі. Цилиндрлік үлгілікті созған кездегі ең қарапайым сызықтық кернеу күйін қарайық. Цилиндрлік үлгілік у осі бойымен Р күшімен тартылсын. Үлгіліктің көлденең қимасында S₀ әсер етуші тік кернеу мынаған тең (оқулық [4] қараңыз):

. (13.2)

Нормалі болатын у осіне α бұрышымен орналасқан еңкіш алаңда тік кернеудің жалғыз ғана сыңары σ_у әсер етеді. Осы сыңар бір жағынан толық нормальды кернеу болып саналып мынандай теңдікпен табылады:

. (13.3)

Толық кернеуді мынандай екі бөлімге бөлуге болады: қиғаш алаңның нормалі бойымен бағытталған тік кернеу; алаңның жазықтығында әсер ететін жанама кернеу 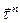. Олардың мөлшері мынандай формулалармен есептеледі:

немесе (13.4)

(13.5)

және

немесе (13.6)

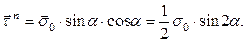(13.7)

Кернеу σ _о басты тік кернеу екендігіне көз жеткізу қиын емес. Өйткені α = 0 болған кезде жанама кернеу 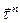жоқ болады ( 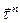= 0), ал толық кернеудің алаң нормаліне проекциясы 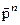ең үлкен мөлшерді алып мынаған тең болады: (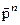)_a=0 = σ_max = σ₁. (13.8)

Жанама кернеу ең үлкен мөлшерді болған кезде алады және мынаған тең болады: .

Осы жағдайда нормальды кернеу тағы да тең болады, өйткені . Нормальды және жанама кернеулердің ең аз мөлшері, олар жоқ болатын (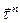 = = 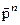0) у осіне паралельді алаңдарда болады.

Сыртқы күштің әсерімен созылатын үлгілікте e_х, e_у, e_z деформациялары пайда болады. Басты бағытта пайда болатын деформациялар e₁, e₂, e₃ басты деформациялар болып саналады. Созу кернеуінің бағытындағы салыстырмалы деформация e₁ таңбасы бойынша оң болады (салыстырмалы ұзару). Оны бойлық деп санау қабылданған, ал e₂ = e₃ деформацияларын көлбеулік деп есептейді.

Сызықтық кернеу күйінің кернеулер, деформациялар және деформациялар жылдамдығы тензорларын қарайық.

Жай созу (орта қысылмайды, e₁ = e, e₂ = e₃ = -0,5 e, e > 0, x₁ = x, x₂ = x₃ = -0,5 x, x > 0, s₁ > 0, s₂ = s₃ = 0):

; ;

Жай қысу (орта қысылмайды, e₁ = e₂ = 0,5 e, e₃ = -e, e > 0, x₁ = x₂ = 0,5 x, x₃ = - x, x > 0, s₃ < 0, s₁ = s₂ = 0):

; ;

.

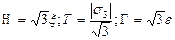Жазық кернеу-деформация күйі. Нормальды кернеулердің сыңары σ₃₃ = 0 деп жобалайық, демек 3 көрсеткішін қосатын жанама кернеулер нөльге тең болады, яғни σ₁₃ = σ ₂₃= σ ₃₁ = 0. Осы себептен жазық кернеу күйі болған кезде тепе-теңдіктің дифференциалдық теңдеулер жүйесі екі теңдеуден тұратын болады, яғни

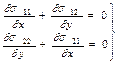,. (13.9)

Еңкіш ВС ауданындағы кернеулерді анықтайық (13.2 сурет). Осы еңкіш алаңдағы нормаль х осімен α бұрышын құрсын. Кубтың ОВ және ОС қабырғаларында σ₁₁ және σ₂₂ нормальды кернеулері және σ₁₂ жанама кернеуі түсірілген. Бағыттаушы косинустар мынаған тең: n ₁ = cosα; n ₂ = sinα; n ₃ = 0.

Бағыттаушы косинустардың мәнін мына теңдеуге қойып

нормальды кернеудің мынандай мәнін аламыз:

(13.10)

Мынандай тригонометриялық байланыстарды қолданып , және 2sinα cosα = sin2α, келесі теңдеуді алуға болады:

, (13.11)

немесе басты кернеумен

(13.12)

13.2 – сурет. Жазық кернеу күйі болған кезде көлбеген алаңдағы кернеулер

Осы теңдеуді келесі түрге өзгертуге болады:

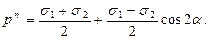(13.13)

Мынандай формулаларды қолданып:

;

жанама кернеуді анықтайтын формуланы табуға болады:

(13.14)

немесе басты кернеумен 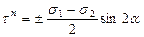. (13.15)

α = 45^о болған кезде жанама кернеу ең үлкен болатындығы осы теңдеуден шығады, яғни .

Осы теңдеу бойынша ең үлкен жанама кернеу басты нормальды кернеулердің жартылай айырмасына тең.

Басты кернеулерді (σ₁ және σ₂) еркін координатты осьтердегі кернеулер σ₁₁, σ₂₂ және σ₁₂ арқылы анықтайтын теңдеулерді шығарайық.

х осінің бағытын нормалі бағытымен сәйкестіріп және мына теңдеулерді ескеріп

; (13.16)

(13.17)

және тағы да сәйкестіргенде pⁿ = s₁₁ және tⁿ = s₁₂ екендігін ескеріп мынандай теңдеулерді аламыз:

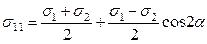; (13.18)

; (13.19)

; . (13.20)

s ₁ мен s ₂ және α анықтау үшін жоғарыда жазылған теңдеулерді бір біріне қосып және алып мынаны табамыз:

s_х + s_у = s₁ + s₂ (13.21)

s_х - s_у = (s₁ - s₂) cos2a (13.22)

(13.22) және (13.20) теңдеулерін екі есеге дәрежелейік және олардың оң және сол жақтарын бір біріне қосайық. Сонда мынандай теңдеуді аламыз:

(13.23)

(13.21) және (13.23) теңдеулерінен мынандай теңдеулерді шығаруға болады:

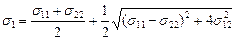; (13.24)

. (13.25)

(13.20) теңдеуді (13.22) теңдеуге бөліп мынаны аламыз:

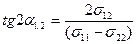. (13.26)

(13.24) және (13.25) теңдеулерді (13.20) теңдеуге қойып мынаны аламыз:

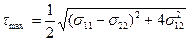. (13.27)

Жазық кернеу күйі үшін басты кернеумен кернеу тензоры мынандай түрді қабылдайды:

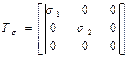. (13.28)

Жазықтық кернеу девиаторы былай анықталады:

. (13.29)

Қаралған жағдай үшін орташа кернеу мынаған тең:

. (13.30)

Деформация процесінде тұтас ортаның материальды бөлшектері координатты жазықтықтардың біреуіне паралельді қозғалуы мүмкін, мысалы х ₁ және х ₂. Осындай жағдайда жылжу векторының сыңарлары мынандай жазық қозғалу өрісін құрайды:

u ₁ = u ₁(х ₁, х ₂); u ₂ = u ₂ (х ₁, х ₂); u₃ = 0. (13.31)

Орын ауыстыру векторларының сыңарларын Грин, Альманси және кіші деформация тензорлары сыңарларын анықтайтын формулаға қою, жазық деформация күйіне сәйкес келетін мынандай деформация тензорларын алуға мүмкіндік береді:

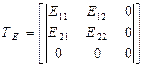; ; . (13.32)

Осы тензорлардың басты сыңарлары үшінші дәрежелі теңдіктерді шешу арқылы анықталады. Жазық деформация болған кезде басты деформацияның біреуі нөльге тең болады. Сондықтан үшінші дәрежелі теңдеулер екінші дәрежесі бар мынандай теңдеулерге айналады:

(13.33)

Осы теңдеулерден, деформация тензорының симметриясын және мынандай қатнастарды Е ₁ ³ Е ₂ ³ Е ₃, L ₁ ³ L ₂ ³ L ₃, e ₁ ³ e ₂ ³ e ₃ ескеріп мынаны аламыз:

(13.34)

Жоғарыдағы формулалар бойынша Е ₁, Е ₂ немесе L ₁, L ₂ анықтауға болады. Ол үшін e₁₁, e₂₂ және e₁₂ кіші деформация тензорларының сыңарларының орнына Грин немесе Альманси тензорларының сыңарларын қойады.

Сонымен басты сыңарлармен жазғанда жоғарыда жазылған тензорлар мынандай түрді алады:

; ; .

Қысылмайтын орта үшін ығысу деформациясының қарқындылығы мынандай формула бойынша анықталады:

. (13.35)

Жазық деформация күйі үшін кернеу тензорын және деформация жылдамдығы тензорын қарайық.

Жазық ағыс үшін (υ₁ = υ₁(x₁, x₂), υ₂ = υ₂(x₁, x₂), υ₃ = 0):

.

Қысылмайтын орта үшін .

Жазық деформация күйі үшін

; .

Қысылмайтын орта үшін

Жазық кернеу күйі үшін (σ ₁₁ = σ ₁₁ (x ₁, x ₂ ), σ ₂₂ = σ ₂₂ (x ₁, x ₂ ), σ ₁₂ = σ ₁₂ (x ₁, x ₂ ), σ ₁₃ = σ ₂₃ = σ ₃₃= 0):

; .

Негізгі әдебиеттер: [1] (тарау 4, бет 101 – 109); [2] (тарау 3, бет 77 – 101); [3] (тарау 1, бет 16 – 75); [4] (тарау 7, бет 163 – 168).

Қосымша әдебиеттер: [6] (тарау 6, бет 3 – 43).

Бақылау сұрақтары:

1. Көлемдік кернеу күйі үшін жеке туындылары бар дифференциальдық теңдеулер түрінде тепе-теңдік шартын қалай анықтайды?

2. Сызықтық кернеу күйі болған кезде көлбеген алаңдағы кернеулер қалай анықталады?

3. Жазық кернеу-деформация күйі үшін дифференциальдық теңдеулер түрінде тепе-теңдік шартын қалай анықтайды?

4. Жазық кернеу-деформация күйі үшін кернеу мен деформация тензорлары қандай тензорлармен жазылады?

5. Жазық кернеу күйі болған кезде көлбеген алаңдағы кернеулерді қалай табуға болады?

6. Жазық кернеу күйі үшін басты кернеулер қалай анықталады?

7. Жазық деформация күйі үшін басты кернеулер қалай анықталады?

 

№14 дәріс. Симметриялық осьті кернеу күйі. Металдар мен қорытпалардың илемділігі.

Металдарды қысыммен өңдеген кезде көлемдік кернеу күйінің өте жиі кездесетін жағдайларының бірі болып симметриялық осі бар кернеу күйі есептеледі.

Кернеу күйінің осы түрі ретінде бетіне немесе бетінің бөліміне таралған күш түскен айналатын дененің кернеу күйі есептеледі. Айтылған таралған күш айналатын дененің осіне қатысты симметриялық орналасады және барлық меридиональды қимада бірдей болады (оқулық [4] қараңыз). Мысал ретінді цилиндрлік дайындаманы шөктіру, осындай дайындаманы қобылау, баспақтау, сымдау және т.б. болуы мүмкін.

Симметриялық осі бар кернеу күйін қараған кезде декарттық координаттың орнына цилиндрлік координатты қолданған өте қолайлы. Цилиндрлік координатта кез келген А нүктесінің жайын ρ (х) осінен өлшенетін радиус вектор ρ -мен, полярлы бұрыш θ -мен және z аппликатасымен анықтайды (оқулық [4] қараңыз). Оқулық [4] келтірілген суреттегі а нүктесі 0 арқылы өтетін және z осіне перпендикулярлы жазықтыққа А нүктесінің проекциясы. Цилиндрлік координатта кернеулерді белгілеу және деформацияланатын денеден бөлінген элементің пішіні 14.1 суретте көрсетілген. Цилиндрлік координаттағы кернеу тензорын мынандай түрде жазуға болады:

.

σ_ρρ кернеуін радиальды деп атайды, σ_θθ кернеуін тангенциальды деп атайды, ал σ_zz кернеуін осьтік кернеу деп айтады.

Симметриялы осі бар кернеу күйінде кернеу сыңарлары θ координатасынан тәуелді емес. Сондықтан тепе-теңдіктің дифференциальдық теңдеуінде осы координат бойынша барлық туындылар нөлге тең болады. Осымен бірге меридиональды жазықтықтарда (z осі арқылы өтетін жазықтықтарда, яғни θ жазықтығында) дененің және сыртқы күштің симметриялығы салдарынан жанама кернеулер пайда болуы мүмкін емес. Сондықтан жанама кернеулердің жұптығын ескеріп мынаны аламыз: τ_ρθ = τ_zθ = τ_θρ = τ_θz = 0. Демек, σ_θθ кернеуі ылғида басты болады, яғни σ_θθ = σ₂, ал ρ осі z жазықтығында кез келген бағытты алуы мүмкін.

Сөйтіп симметриялы осі бар кернеу күйі үшін кернеу тензорын былай жазуға болады:

Бар болғаны үш нормальды және бір-біріне тең екі жанама кернеулер тензорда бар.

Декарттық координаттарда көлемдік кернеу күйін қараған кезде қолданылған математикалық әдісті тағы да қолданып симметриялық осі бар кернеу күйі үшін цилиндрлік координатта дифференциальдық тепе-теңдік теңдеуін шығарайық.

.

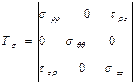Әсер етуші кернеулер 14.2 суретте көрсетілген. ρ осін z жазықтығындағы кез келген бағытта жүргізуге болатындын бұрын айтылды. Есептеуді жеңілдету үшін осы осьті 14. суретте ρz жазықтығы бөлінген элементарлы көлем үшін симметриялы жазықтық болатын етіп жүргізген.

14.1 – сурет. Цилиндрлі координаттарда кернеулерді белгілеу

14.2 – сурет. Цилиндрлі координаттарда әсер ететін кернеулер

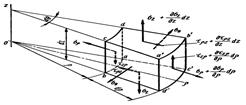
Элементарлы аудандардың аудандары мынандай болады:

F _ρ = ρ d θ d z; F _ρ+dρ = (ρ + d ρ)d θ d z; F _θ = d ρ d z; F _z = ρ d θ d ρ.

Элементке әсер ететін барлық күштерді ρ және z остеріне проекциялап тепе-теңдік шартын былай жазайық ():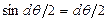

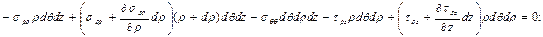
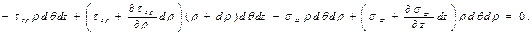
Жоғарғы ретті шексіз кішкентай мөлшерлерді ескермей алгебралық өзгерту және қысқартудан кейін мынаны аламыз:

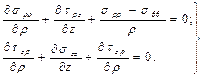
Симметриялық осі бар кейбір есептерді шығарған кезде цилиндрлік координатпен бірге сфералық координатты қолдануға тура келеді. Осы жүйеде нүктенің орналасатын жерін радиус вектор ρ -мен және нүктенің жайын кеңістікте анықтайтын θ және φ бұрыштарымен табады (оқулық [4] қараңыз).

Осы жағдай үшін кернеу тензорында келесі түр бар болады:

.

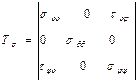Симметриялық осі бар кернеу күйі кезінде кернеу θ координатасынан тәуелді емес, ал көрсеткіштерінде осы координат бар жанама кернеулер нөльге тең болады, яғни σ_ρθ = σ_θρ және σ_φθ = σ_θφ.

Симметриялық осі бар кернеу күйі үшін сфералық координаттағы тепе-теңдіктің дифференциальды теңдігі мынандай теңдеумен жазылады (шығарусыз келтірілген):