Мора кернеуінің диаграммасы 3 страница

және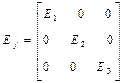

төмендегі сипаттамалық теңдеулерден анықталады:

(8.15)

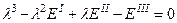, (8.16)

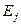мұндағы λ – және -дің басты мәндері; 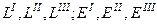– 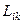және 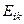тензорларының сәйкесті бірінші, екінші, үшінші инварианттары.

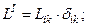
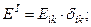
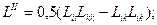
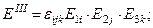
Деформация процесінде элементарлы сфера эллипсоидқа айналады. Бұл бейнелеудің жергілікті аффиностілігінен келіп шығады. Осындай сфераның эллипсоидқа айналатандығын дәлелдеу мақсатымен дефорцияланбаған ортадан радиусы 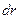болатын сфералық бетпен шектелген материалдық көлемді алайық. Бастапқы координаттағы осындай беттің теңдеуі мынандай болады: .

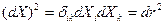Деформация жасалғаннан кейін сол материалды көлемнің беттік теңдеуі мынандай түрді қабылдайды:

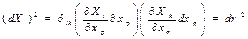немесе

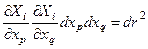. (8.17)

Осы теңдеу деформацияның материалды эллипсоиды ретінде белгілі 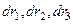жартылай осьтері бар эллипсоидты анықтайды.

Эллипсоидтың жартылай осьтері мынандай қатнаста болсын: . Онда (8.15) теңдеуінен анықталатын басты деформациялар мынаған тең болады:

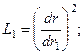
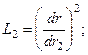
. (8.18)

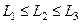Сөйтіп теңсіздігінен теңсіздігі шығады. Сондықтан ең үлкен деформацияға 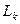-ның ең кішкентай мәні сәйкес келеді.

Сірә, қос нәтижелік сырт пішінді өзгерту тензорларының басты мәндері мынандай қарапайым қатнастарымен байланысты:

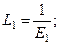
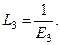(8.19)

Логарифмдік деформацияны есептеп мынаны аламыз:

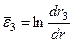; ; (8.20)

және қарауымызға мынандай логарифмдік деформацияның тензорын енгіземіз:

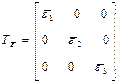(8.21)

Осы тензордың басты осьтері материалды эллипсоидтың осьтерімен дәл келеді және 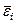-дің басты сыңарлары басты логарифмдік деформация деп аталады.

Еркін координат жүйесіндегі тензор сыңарларын (8.8) және (8.14), содан кейін (8.4) және (8.12) формуларының қолданып табуға болады.

Нәтижелік сырт пішінді өзгерту тензорларының 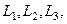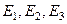сыңарлары логарифмдік деформациялар арқылы былай көрсетіледі:

(8.22)

Сөйтіп басты логарифмдік деформацияны анықтау үшін бір нәтижелік сырт пішінді өзгерту тензорының сыңарларын (Коши деформациясы тензорының сыңарларын) және осы тензордың басты мәнін табу қажет.

Қысылмаушылық шарты қалай жазылатындығын қарайық. Деформацияға дейінгі элементарлы сфераны көлемі мынаған тең: 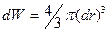, ал материалды эллипсоидтың көлемі былай табылады: 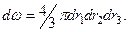Осы көлемдерді теңестіре отырып және алынған теңдіктің екі жағын да логарифмдеп мынандай формуланы аламыз: 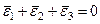, (8.23)

яғни логарифмдік деформациялардың қосындысы нөльге тең болады.

Логарифмдік деформацияны толығырақ зерттеу үшін тікбұрышты параллелепипедтің біркелкі деформациясын қарайық. Параллелепипедтің басстапқы енін, ұзындығын және биіктігін 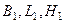әріптерімен, ал деформацияның ағымдағы уақытысындағы осы параллелепипедтің енін, ұзындығын және биіктігін 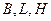әріптермен белгелейік.

Параллелепипедтің ақырғы өлшемдері болып саналатын болсын (8.2 сурет). Параллелепипед биіктігіне шөктірілді деп есептейік. Осы шөктеруге сәйкесті шексіз кішкентай салыстырмалы деформация мынаған тең болады: .

8.2 – сурет. Тікбұрышты параллелепипедтің біркелкі деформациясы

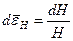биіктігінен 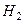биіктігіне дейін шөктерген кезде салыстырмалы деформацияның жиынтығы мынаған тең болады: 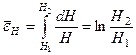. Осы деформацияға ұқсайтын ен мен ұзындық бағыттарындағы деформациялар былай анықталады: ; .

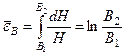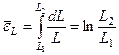Сөйтіп біркелкі деформация кезінде логарифмдік деформацияны табу үшін өте шексіз кішкентай деформациялардың қосындысын табу керек. Сондықтан, логарифмдік деформацияны көп жағдайда дәл деформация деп атайды.

Дененің деформациядан кейінгі өлшемдерін осы өлшемдерге сай деформацияға дейінгі өлшемдерге қатнастырып мынандай коэффициенттерді табады: 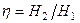– шөктеру коэффициенті (жаншу); 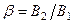– кеңейту коэффициенті; 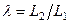– ұзарту коэффициенті (ұзарту).

Дененің көлемі тұрақты болған кезде мынандай теңдік орынды болады: Осы теңдіктің оң жағын сол жаққа бөлген кезде мынаны табуға болады: .

Жоғарыдағы теңдіктің екі жағында логарифмдесек материалдың қысылмаушылық шартын мынандай түрде табамыз: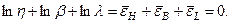

Негізгі әдебиеттер: [1] (тарау 2, бет 49 – 77); [4]: (тарау 3, бет 111 – 134).

Қосымша әдебиеттер: [6] (тарау 3, бет 38 – 58).

Бақылау сұрақтары:

1. Грин тензоры қандай формуламен анықталады?

2. Альмансы тензоры қандай формуламен анықталады?

3. Логарифмдік деформацияның тензорын қандай ретпен анықтауға болады?

4. Шөктеру, кеңейту, ұзарту коэффициентерінің көбейтіндісі неге тең?

5. Шөктеру, кеңейту, ұзарту коэффициентері қандай формуламен анықталады?

 

№9 дәріс. Кішкене деформацияның тензоры

Енді жалпы танысудан бас тартып орын ауыстырудың сыңарлары және олардың градиенттері кішкентай деп есептейміз.

Сонымен қатар 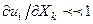деп есептеп (8.8) формуласындағы осы мөлшерлердің көбейтіндісін алып тастауға болады. Нәтижесінде мынандай сыңарлары бар лагранждық кіші деформация тензорын аламыз: .

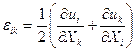Осыған ұқсас 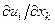бірмен салыстарғанда кіші деп есептеп (8.14) формуласында олардың көбейтіндісін алып тастап мынандай сыңарлары бар эйлерлік кіші деформация тензорын аламыз: .

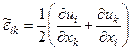Ығысуды кішкентай деп болжау лангранждық және эйлерлік координаттар арасында айырмашылық жоқ, ал сәйкесті тензорлар бір-біріне дәл келеді деп есептеуге әкеледі, яғни .

Ары қарай, кішкене деформация теориясында тек лангранждық координат қолданалатын болады және уақыттың мынандай екі кезеңін қарайтын боламыз: бастапқы 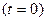және түпкі .

Материалды бөлшектің соңғы жайын (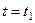 болған кезде) орын ауыстыру векторының көмегімен анықтайтын боламыз. Осы, материалды бөлшектің бастапқы (лангранждық) координаталарын 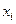кіші әріпімен жаза отырып белгілеу жүйесін өзгертуге мүмкіндік береді. Сонда орын ауыстырудың векторлық өрісі мынандай түрде жазылады: .

Деформация тензоры. Мынандай симметриялық тензор: (9.1)

сызықтық кішкене деформация тензоры немесе жай кішкене деформация тензоры деп аталады. Мұндағы кішкене деформация тензорының сыңарлары мынандай формуламен анықталады: 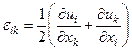. (9.2)

Осы тензордың сыңарларында қандай геометриялық мағана бар екендігін қарастырайық. Бұрын біз М және N бөлшектерін толық еркін орналастырдық. Енді 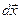векторы 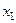осіне параллельді болатын етіп N бөлшегін таңдайық, яғни .

Деформациядан кейін 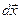векторы 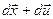векторына түрленеді, әрі 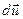векторының сыңарлары (9.2) формуласы бойынша есептеледі.

М және N бөлшектері арасындағы деформацияға дейінгі ара қашықтық L әріпімен, ал деформациядан кейінгі ара қашықтық l әрпімен белгілейік. Сонда мынаны аламыз:

.

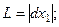
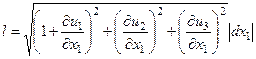Бұрынырақ біз талдауды кішкене деформация жағдайымен шектедік. Бұл шексіз кішкене ретке дейінгі дәлдікпен мынаны жазуға мүмкіндік береді:

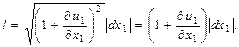
МN материалды кесіндінің салыстырмалы ұзаруы мынаған тең болады:

.

Сонымен 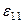сыңары деформацияға дейін 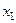осіне параллельді болатын элементарлы кесіндінің салыстармалы ұзаруына тең.

Осыған ұқсас, және 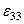сыңарлары, сәйкесті 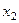және осьтеріне параллельді материалды кесінділердің салыстырмалы ұзаруына тең болады.

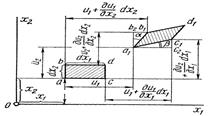
Деформацияланатын дененің қандай болса да М нүктесінде координат осьтеріне параллельді шексіз кішкентай және 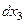қыры бар элементарлы параллельді бөлейік. Осы параллепипедтің бір ұшы М нүктесімен дәл сәйкес келуі керек.

осы элементарлы параллелепипедтің деформацияға дейінгі жазықтығына, ал а нүктесі М нүктесінің проекциясы болсын (9.1 сурет).

Деформациядан кейін а, b, c, d нүктелері орын ауыстыруды алды. а нүктесі 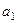нүктесіне, b нүктесі 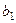нүктесіне, с нүктесі 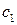нүктесіне, d нүктесі 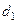нүктесіне ауысады. 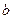және с нүктелерінің орын ауыстыруларын а нүктесінің орын ауыстыруы арқылы білдірейік. 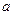нүктесі 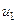және 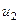орын ауыстыруларын алды. Осы орын ауыстырулар, 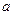нүктесі проекциясы болатын М нүктесінің координатасының функциясы болады, яғни ; . с нүктесі 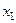осінің бағытында 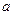нүктесінен шексіз кішкентай 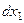ара қашықтығында орналасқан. Сондықтан 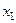осінің бағытында с нүктесінің 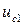орын ауыстыруы мынаған тең болады: Бірақта жоғарлы қатарлы мүшелерді ескермей 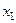осінің бағытында с нүктесінің орын ауыстыруы 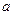нүктесінің орын ауыстыруынан 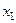координатасы бойынша 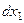ұзындығында 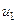функциясының қосымша өсірілу мөлшеріне айырмашылықта болады деп есептеу керек. Онда мынаны аламыз: .

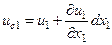Осыдан, ұзындығы 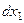болатын 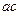қырының салыстырмалы ұзындығы, яғни 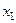бағытындағы 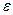салыстырмалы деформациясы мынаған тең болады:

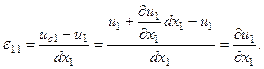
Осыған ұқсас жолмен мынаны аламыз:

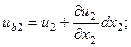
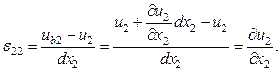
9.1 суретті қолданып тағыда мына орын ауыстыруларды анықтауға болады:

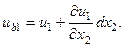
Енді бұрыштық деформацияларды анықтауға ауысайық.

Бұраштардың өзгеруі шексіз кішкентай болғандықтан мынандай шарттарды қабылдаған дұрыс болады: 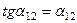және 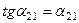. Сондықтан осы бұрыштарды мынандай формуланы қолданып анықтаймыз (9.1 сурет): .

9.1 – сурет. Элементарлы параллелепипедтің координаталық осьтер проекциясындағы сызықтық және бұрыштық деформациясы

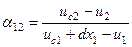Осы формулаға және 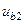-нің алынған мәндерін қойып мынаны табамыз:

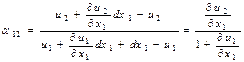
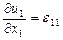және осы мөлшер бірден едәуір кіші болғандықтан мынаны жазған әділ болады: Осындай тәсілмен мынаны аламыз: .

Сонымен және 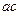кесінділердің арасындағы бастапқы кездегі тік бұрыш мынандай мөлшерге азайады: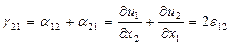

Тік бұрыштың осындай өзгеруі оның салыстырмалы ығысуы деп аталады.

Қаралып жатқан параллелепипедтің басқа координатты жазықтықтарға проекциялары үшін ой бағытын жалғастырып, деформация тензорының бүйірлік сыңаралары және бұрыштардың бұрмалануын сипаттайтындығын оңай байқауға болады. Осы деформация тензорының сыңарларын ығысу деформациясының сыңарлары деп атайды.

Қаралып жатқан параллелепипедті 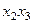және жазықтықтарына проекциялап деформацияның басқа сыңарларын анықтайтын формулаларды табамыз.

Нәтижесінде мыналарды аламыз: салыстармалы ұзару ; ; ;

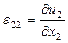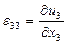салыстармалы ығысу .

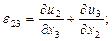
Деформация тензорының 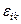сыңарларының таңбасын талдауға тоқталып өтеуік.

Егер 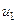функциясы 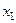өскен сайың үлкейсе, яғни 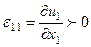, онда біз, сірә 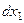ұзындығының өсуіне куә боламыз (9.1 суретте с бөлшегінің оңға қарай орын ауысуы а бөлшегінің орын ауысуынан көп болады). Сонымен егер 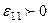болса, онда ұзару бар болады, ал егер 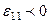болса, онда деформация кезінде материалды талшық қысқаратын болады.

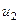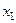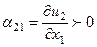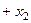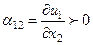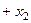Ары қарай, егер функциясы өскен сайың көбейетін болса, онда болады. Сонда ас кесіндісі осінен осіне қарай бұрылатын болады (9.1 - сурет). Дәл осылай болған кезде кесіндісі осінен 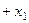осіне қарай бұрылатын болады. Осыдан егер және 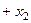осінің арасындағы тік бұрыш азайатын болса онда ығысуы оң болатындығы шығады. Осы ереже басқа жазықтықтардағы ығысулар үшін әділ болып қалады.

Сонымен 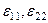, 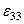оң сызықтық деформацияларға координат осьтері бойымен ұзару сәйкес келеді, ал теріс сызықтық деформацияларға айтылған координат осьтері бойымен қысқару сәйкес келеді.

Оң , ығысуы деформацияларына осьтердің оң бағыттары арасындағы бұрыштардың кішіреюі сәйкес келеді, ал теріс ығысуы деформацияларына айтылған бұрыштардың көбеюі сәйкес келеді.