Реология туралы. Анықтайтын теңдіктердің жалпы теориясын жасау тұтас орта механикасының маңызды бөлімі болып саналатын реалогияның ең негізгі міндеттері болып есептеледі (рео – ағу грек сөзі, материальдардың ағысы туралы ғылым). Реология мынандай сұраққа жауап беруі қажет: белгілі деформациялау (күш түсіру) процестерінде t уақыт мезгілінде берілген материальды бөлшек айналасында қандай кернеулер (деформациялар) пайда болады. Дәлірек айтсақ реология мынандай функционалдар түрін анықтайды:
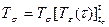немесе 
.
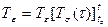Осы функционалдар әр түрлі тұтас ортаның термомеханикалық қасиеттерін бейнелейді. Осындай есептерді шығару, заттардың іс жүзіндегі термомеханкалық қасиеттерін бейнелеуге мүмкіндік беретін көптеген зерттеу тәжірибелерін және реологиялық модельдерді жасауды қажет етеді.
Зерттеу тәжірибелеріне көңіл бөлейік. Материалдардың маңызды және әдеттегі қасиеттерін цилиндрлік үлгіліктерді созу тәжірибесі бойынша табуға болады. Біркелкі кернеулер мен деформациялар күйін үлгіліктің ортанғы бөлімінде алу мақсатымен дөңгелек цилиндрлік үлгіліктің есептеу ұзындығын l о оның диаметрінен d о бес немесе он рет үлкен болатын етіп жасайды.
Әдетте, сынау үшін алдыңғы созу диаграммасын автоматты түрде салуға мүмкіндік беретін үзілу машиналарын қолданады. Осы диаграммада ординат осі бойымен күш Р -ны, ал абсцисса осі бойымен күшке сәйкес келетін ұзаруды (Δ l) салады.
Шартты және дәл кернеулер диаграммасы (11.1 - сурет). Координаталары Р – Δ l болатын созу диаграммасының түрі материалдардың тек қасиетінен ғана емес, ал тағы да тәжірибе жасайтын үлгіліктің өлшемінен өте үлкен тәуелді болады. Материалдардың тек механикалық қасиетін сипаттайтын диаграмманы алу үшін алдыңғы созу диаграммасын координатасы σ – ε болатын диаграммаға қайта есептейді. Осы диаграмманың ординатасын созатын күш Р -ны сынайтын үлгіліктің бастапқы көлденең қимасы ауданына бөліп табады, яғни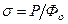 
.
Кернеу диаграммасының абсциссасын үлгіліктің есептеу бөлімінің абсолютті созылуын, осы үлгіліктің бастапқы ұзындығына бөліп анықтайды, яғни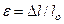 
.
Осындай әдіспен табылған кернеу мен деформацияның арасындағы байланыс графигі үлгілікті созған кезде өзгеретін көлденең қиманың ауданын есепке алмайды. Сондықтан осы график кернеудің шартты диаграммасы деп аталады. Жоғарыда айтылған диаграммадан айырмашылығы бар болатын дәл кернеу диаграммасын салғанда, созған кезде өзгеретін үлгіліктің көлденең қимасының ауданын есепке алады. Дәл кернеу диаграммасын салған кезде күш Р -ны созғанда өзгеретін көлденең қиманың сәйкесті ауданы Ф -ға бөледі.
11.1 суретінде төмен көміртегілі болаттар үшін шарты (тұтас сызық) және дәл (сызықша сызық) кернеулер диаграммасы келтірілген. Әрбір сызықта А, В, С, D, Е, F сияқты бір қатар ерекше нүктелердің бар екендігін айтып кетуге болады. Бастапқы ОА бөлімде диаграмма еңкейген түзу сызық түрінде көрсетіледі. Осы шекте кернеу (σ) деформацияға (ε) пропорционалды өседі, яғни мынандай Гук заңы сақталады: σ = Еε, мұндағы Е – үлгілікті созған кездегі серпімділік модулі.
Гук заңы пропорционалдықтың шегіне (σпц) дейін дұрыс болады.
Диаграмма А нүктесінен жоғарғы жақта қисаяды, осы кезде Гук заңы бұзылады. Бірақта серпімділік шегіне (σуп) сәйкес келетін В нүктесіне дейін үлгіліктің деформациясы серпімді болып қалады және күшті алған кезде толық жоғалып кетеді. Нүктелер А мен В -ның арасы өте жақын, сондықтан оларды көп жағдайда сәйкес келеді деп санайды. Егер В нүктесі арқылы тік сызықты сызса, онда бұл сызықтың сол жағында серпімді деформациясының аймағы, ал оң жағында серпімді-илемді деформацияның аймағы бар болады. Өйткені серпімділік деформциясымен бірге күшті алғаннан кейін үлгілікте қалатын илемді деформацияға орын бар болады.
Диаграммада С нүктесінен басталатын көлденең бөлім пайда болады. Бұл бөлім ағым шегі (σs) деп аталады. Осы бөлімде күш ұлғаймай деформация үлкейіп отырады. Материал аққан сияқты болады. Сондықтан СD бөлімін жиі ағым ауданы деп атайды.
Көптеген материалдарда ағым ауданыны жоқ болады, яғни көптеген жағдайларда материалдарды созуға сынаған кезде СD ауданы байқалмайды және созу диаграмасы суретте көрсетілген қисық сызық түріне ие болады. Бұл жағдайда ағым шегін σs шартты түрде табады.
11.1 суретке қайта оралайық. Материал D нүктесінен бастап деформацияға кедергісін үлкейтеді. Бірақта үлгілік созылған кезде күштің үлкею серпімділік бөлімімен салыстырғанда өте кішкентай болады. Диаграмма жатық қисық сызықпен өзгеріп Е нүктесіне жетеді. Диаграмманың осы Е нүктесінде шартты кернеу (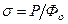) ең үлкен мөлшерге жетеді. Осы мөлшер уақытша кедергі σв деп аталады.
Диаграммада Е нүктесіне жеткеннен кейін үлгілікте болашақта үзілетін орын белгіленеді және мойын, яғни үлгіліктің жергілікті тарылуы пайда болады. Үлгіліктің көлденең қимасы кішірейгендіктен диаграммада шартты кернеу азаяды. Бірақта, егер мойынның ең кішкентай қима ауданына қатысты етіп дәл кернеуді есептесе, онда үзілу уақытысына дейін (
нүктесі) кернеудің өсуі байқалады.
Мойынның пайда болуы, осы мойындағы қимадан қимаға және әрбір қимада деформацияның біркелкі еместігімен қошталатындығын айта кету қажет.
Жүктен босату және қайтадан жүктеу. Шарты диаграмманың К нүктесіне жеткеннен кейін зерттейтін үлгілікке беретін күшті азайтайық. Күштен босатқан кезде σ – ε байланысы КL түзу сызығымен көрсетіледі. Айтылған КL сызығы ОА сызығына параллельді болады. Серпімді-илемділік деформация аймағында күштен босатқан кезде деформация толық жоқ болып кетпейді. Осы деформация серпімді бөлімі мөлшеріне (LМ кескіні) азайады. Қалдық немесе илемділік деформациясын ОL кескіні көрсетеді.
Үлгілікті қайта жүктегенде созу диаграммасы LК түзуінің түрін қайта алады, ал ары қарай КЕF қисық сызығының үстімен жүреді. Сонымен металл бірінші деформацияның себебінен серпімділік қасиетін алады және серпімді шегі үлкейеді. Осымен бірге илемділік деформация қасиеті біраз төмендейді. Бұл құбылысты беріктену деп атайды. Цилиндрлік үлгілікті қысқанда немесе бұрағанда осы сияқты кернеу диаграммасын алуға болады.
|
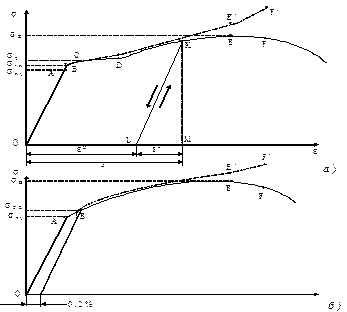
Деформация жылдамдығының әсер етуі. Кернеу диаграммасына деформация жылдамдығының әсер етуі температурамен тығыз байланысты болады. Бұның себебі J р температурасында (балқудың абсолюттік температурасының 0,4 жуықты тең болатын) және одан жоғары температурада деформацияланған металда белгілі бір жылдамдықпен рекристаллизация процесі жүреді. Бұл процесте жаңа түйіршіктер пайда болады және поликристалдың бір кристалдық түйіршіктері басқа түйіршіктерді пайдаланып өседі. Рекристаллизация процесінде металдар термодинамикалық тұрақты күйге өтеді.
Осы процесті үш сатыға бөледі. Бірінші сатысында деформацияланған поликристалда жаңа кристалдық түйіршіктер пайда болады. Осы түйіршіктер деформацияланып бұрмаланған түйіршіктерді сіңіру арқылы өседі. Екінші сатысын жинақтаушу рекристаллизация деп атайды. Жинақтаушы саты жүрген уақытта бұрмаланған түйіршіктердің біреулері басқалары арқылы үлкейеді. Осының себебінен түйіршіктердің орташа мөлшері үлкейеді. Үшінші сатыда мөлшерін үлкейтуді кейбір жеке түйіршіктер ғана көрсетеді. Осының әсерінен металдың құрылымында әр түрлі өлшемі бар түйіршіктер пайда болады.
Рекристаллизация металл құрылымының кемістігін жойады, металдың илемділік қасиетін үлкейтеді, деформацияға дейінгі қасиеттерін және текстураны қалпына келтіреді.
Сонымен, рекристаллизация температурасынан жоғарғы температурада қыздырылған дайындаманы илемді деформациялаған кезде (осындай деформацияны «ыстық» деп атайды) беріктенумен қатар беріксіздендіру процестері жүреді. σ – ε диаграммасы сызықтарының түрлері осы екі процестер жылдамдықтарының ара қатысымен тығыз байланысты. Егер деформация жылдамдығы үлкен болса, онда беріксіздендіру процесінің ықпалы аз болады. Бұл кезде материал тұтқырлы қасиет көрсетеді. Серпімді-илемді деформация аймағында деформация жылдамдығы өскен сайын кернеу үлкейеді. Қарапайым жағдайларда мынандай сызықтық байланыс пайда болады: σ = σs + m x, мұндағы m - тұтқырлық коэффициенті. Егер σs = 0 болса, онда сызықты-тұтқырлы материалға келеміз (Ньютон ортасы). Сонымен материалдың температурасымен байланыстыра отырып илемділік деформациясы туралы мынаны айтуға болады: металдың «ыстық» деформациясы (J > J р); металдың «суық» деформациясы (J < J р); металдың жылы деформациясы (J» J р).
Температураның және деформация жылдамдығының кернеу диаграммасына әсер етуін әдейілеп жасалған сынау машинасын (пластометр) қолданып зерттейді. Осы машинада дайындаманы қысқанда немесе созғанда деформация жылдамдығын тұрақты ғып зерттеу жүргізуге жағдай жасалынады.
Қарапайым реологиялық модельдер. Цилиндрлік үлгіліктерді созу тәжірибелерінің нәтижелерін қарай отырып біз материалдардың мынандай қасиеттерін айыттық: серпімділік, тұтқырлық, илемділік. Сыртқы күш әсер еткенде тұтас ортаның көрсететін ерекше қасиеттерін жоғарыда айтылған үш іргетасты қасиеттерді қисындастыру арқылы көрсетуге болады.
Осыған байланысты кейбір дәріптелген ортаның жүріс-тұрысын механикалық элементермен шарты түрде бейнелеп суреттейтін қарапайым реологиялық моделдерді енгізген дұрыс. Бұрынғыдай сызықтық кернеу күйін қарайтын боламыз (сырықты созу). Мынандай белгілеуді енгізейік: σ – тиісті кернеу; ε – салыстырмалы ұзару; x = d ε /d t – салыстырмалы ұзарудың жылдамдығы.
Сызықты-серпімді ортаның моделі Гук заңына былай бағынады:
σ = Еε. (11.1)
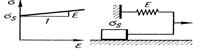
Осы модельді шарты серіппе түрінде бейнелейтін боламыз (11.2, а сурет).
Сызықты-тұтқырлы ортаның моделін мынандай Ньютонның тұтқырлық заңымен көрсетуге болады:
. (11.2)
Осы модельді цилиндрдің ішінде қозғалатын поршень түрінде бейнелеуге болады. Айтылатын нәрсе, ол цилиндрдің іші тұтқырлы сұйықпен толып тұрғаны және тұтқырлы сұйықтың поршень мен цилиндрдің қабырғасы арасындағы саңлаудан шығатыны (11.2, б сурет).
|
Қатаң-илемді ортаның моделін бейнелегенде ағым шегінен төменгі кернеуде дефоромация жоқ деп есептейтін боламыз, яғни ағым шартын қанағаттандыратын кернеуде илемді ағыс бар деген шешімді қабылдаймыз, яғни
σ = σs. (11.3)
Осы модельді жазықтықта тыныш тұрған салмақ түрінде көрсетеміз (құрғақ үйкеліс элементі, 11.2, в суреті).
Енді қарапайым түрде қиыстырылған модельдерді қарауға көшейік. Серпімді және илемді элементерді тізбекпен қосайық. Қорытындысында серпімді-илемді ортаның моделін аламыз. Осы ортаның σ – ε диаграммасы 11.3 суретінде көрсетілген.
Осы жағдай үшін жалпы деформация мынандай екі бөлімнен тұрады:
ε = εе + εр. (11.4)
мұндағы εе – серпімділік деформациясы; εр – илемділік деформациясы.
Үлгіліктен күшті алған кезде серпімділік деформациясы жоқ болады, ал илемділік деформациясы қалады. 11.4 суретте сызықты беріктенетін қатаң-илемді ортаның, ал 11.5 суретте сызықты беріктенетін серпімді-илемді ортаның σ – ε диаграммалары келтірілген.
|
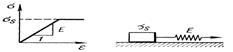
Серпімді және тұтқырлы элементерді тізбекпен қосайық (11.6 сурет). Деформация жылдамдығы x = dε/dt төмендегідей серпімділі құрамның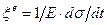 
және тұтқырлы құрамның 
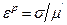қосындысынан тұрады:
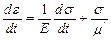. (11.5)
Жоғарыда жазылған теңдеу Максвелдің серпімді-тұтқырлы орта моделіне сәйкес келеді. Осы ортаның кейбір қасиеттерін қарайық. Кернеу тұрақты болсын (σ = const). Онда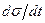 
= 0 және материал тұтқыр сұйық сияқты ағады.
Енді үлгіліктің екі жағында бекітейік және t = 0 уақытысында кернеуді осы үлгілікке түсіріп деформацияны анықтайық. Бұл жағдайда dε/dt = 0 болғандықтан жоғарыда жазылған теңдікті мынандай түрмен жазуға болады: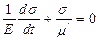 
.
|
|
Соңғы теңдеуден мынаны алуға болады:
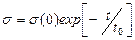, (11.6)
мұндағы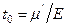 
мөлшерін релаксация уақыты деп атайды. Релаксация уақыты дегеніміз бастапқы кернеудің е = 2,718 рет азайуына кететін уақыт. Сонымен Максвелл ортасының моделі нақты дененің маңызды қасиеттерін бейнелеуге мүмкіндік береді. Бұл қасиет бойынша өзгермейтін деформацияда кернеу экспоненциальды заңмен азайады.
|
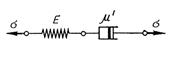
Серпімділі және тұтқырлы элементерден тұратын параллельді құраманы талдауға көшейік (11.7 сурет). Осы модельді серпімді-тұтқырлы Фойгта ортасы деп атайды. Сірә, кернеу төмендегідей серпімділі σе = Еε және тұтқырлы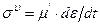 
құрамның қосындысынан тұрады:
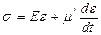. (11.7)
(11.5) теңдеунен айырмашылықта болатын (11.7) теңдеуі релаксация процесін сипаттамайды. Оның себебі деформация тұрақты болғанда (ε = const) кернеуде тұрақты болады, ал орта серпімді сияқты болады. Егер кернеу тұрақты болса, онда деформация мынандай заңдылықпен бірқалыпты өседі:
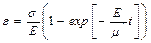. (11.8)
Осылай өскен кезде деформация σ/Е мәніне ұмтылады, яғни жылжыпсырғымалылық пайда болады.
|
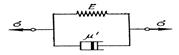
Тұтқырлы және илемді қасиеттерден тұратын модельді қарайық. Бірінен кейін бірі қосылған екі элемент (тұтқырлы және илемді) тұтқырлы-илемді орта моделіне алып келеді. Егер σ < σs болса, онда осы модель сызықты-тұтқырлы ортаның қасиеттеріне ие болады, ал егер σ = σs болса, онда ол өте жақсы илемді дене сияқты ағады.
Тұтқырлы және илемді элементерді параллельді қосқанда да тұтқырлы-илемді ортаны алады (Шведов-Бингмен ортасы). Осы ортаның қасиеттерін мынандай теңдікпен жазуға болады:
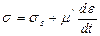(σ ≥ σs болған кезде) (11.9)
Егер σ < σs болса, онда деформация жоқ деп есептейді.
Материалдарды әр түрлі температурада бір осьті жағдайда созып сынау жанама кернеулер қарқындылығы мен ығысу деформацияларының қарқындылығы арасында Т = Т (Г) және жанама кернеулер қарқындылығы мен деформация жылдамдықтарының қарқындылығы арасында Т = Т (Н) байланыстар диаграммаларын алуға мүмкіндік береді (оқулық [4] қараңыз). Осылай созған кезде қысылмайтын материал үшін сызықтық кернеу күйінің сұлбасын іске асырып мынаған ие боламыз: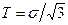 
, 
, 
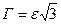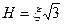. Жазылған формулаларды қолданып σ - ε немесе σ - x қисық сызықтарын Т = Т (Г) немесе Т = Т (Н) қисық сызықтарына жеңіл ауыстыруға болады.
Негізгі әдебиеттер: [1] (тарау 6, бет 142 – 175); [4]: (тарау 6, бет 221 – 271).
Қосымша әдебиеттер: [6] (тарау 5, бет 71 – 88).
Бақылау сұрақтары:
1. Реология дегеніміз не?
2. Осы реалогия ғылымы қандай сұрақтарды оқып зерттейді?
3. Қандай қарапайым реологиялық модельдерді Сіз білесіз?
4. Жылжыпсырғымалылық дегеніміз не?
5. Кернеудің релаксациясы дегеніміз не?
№12 дәріс. Серпімділік және тұтқырлық. Илемділік.
Көлемдік кернеу күйі. Біз қарапайым реологиялық модельдерді қарап шықтық (сызықты-серпімділі, сызықты-тұтқырлы, қатаң-илемді және т.б.). Ортаның қасиеттерін сипаттайтын бұл теңдеулер сызықтық кернеу күйінің жеке жағдайларына жатады.
Көлемдік кернеу күйі кезінде осы орталардың жүріс-тұрысын бейнелейтін жалпы байланыстарға ауысқан кезде кернеулер, деформациялар және деформациялар жылдамдықтары арасындағы байланыстарды анықтау қажет, ал тағы да илемділік шартын жазу керек. Табылған байланыстар сызықтық кернеу күйіне ауысқан кезде жоғарыда зерттелген байланыстарға алып келуі қажет, ал жалпы жағдайда анықтаушы теңдеулер теориясының негізгі принциптерін орындау керек және тәжірибемен жақсы сәйкес келуі қажет.
Екі симметриялық тензорлардың функциональды байланыстарының мүмкін болатын түрін айқындайық.
Айтылған тензорлардың біреуі ретінде кернеу тензорын Т σ (σ кернеулеріне сәйкес келетін) қабылдайық. Екінші тензордың ролін деформация тензоры Т ε (ε деформацияларына сәйкес келетін) немесе деформация жылдамдығы тензоры (ξ деформация жылдамдықтарына сәйкес келетін) орындайтын болады.
Сызықты-серпімді орта. Кернеулер мен деформациялар арасындағы сызықтық изотропты байланыста мынандай түр бар болады: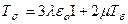 
(12.1)
немесе скалярлы түрде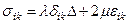 
, (12.2)
мұндағы Δ = 3εо = ε11 + ε22 + ε33 – көлемнің салыстырмалы өзгеруі.
Осы теңдеуді Гуктың қорытынды теңдеуі деп айтады. Айтылған теңдеу сызықты-серпімді ортаның жүріс-тұрысын бейнелейді. Тұрақты мөлшерлерді (λ және μ) Лямэнің серпімді тұрақтысы деп айтады.
Көрсетілген қатнастарды оларға эквиваленті түрде жазып Гук заңының мынандай екінші түрін аламыз: σ = k Δ, (12.3)
D σ = 2 μD ε. (12.4)
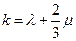коэффициентін көлемдік қысудың модулі деп айтады.
Сонымен, сызықты-серпімді орта үшін орташа кернеу көлемнің салыстырмалы өзгеруіне пропорцональды, ал кернеу девиаторы деформация девиаторына пропорцональды.
Сызықты кернеу күйі жағдайына қайта оралайық. Мынаны негізге алып:
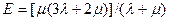, (12.5)
(12.2) теңдеуінен төмендегідей түрде Гук заңын аламыз: 
. Таза ығысу болған жағдайда Гук заңы былай жазылады: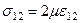 
. Сондықтан μ коэффициенті материалдар кедергісі пәнінен жақсы белгілі ығысу модулі болады.
Сызықты емес-серпімді орта. Егер серпімді материал Гук заңына бағынбайтын болса, онда сызықты кернеу күйі болған кезде σ – ε байланысы сызықты емес функция σ = f (ε) түрін алады (12.1, а сурет). Осындай жағдайда күшті түсіргенге және күштен босатқанға бір ақ қисық сызық ОА сәйкес келеді. Күштен босатқаннан кейін деформация нөльге тең болады. Бұндай материалды сызықты емес-серпімді деп атайтын боламыз.
|
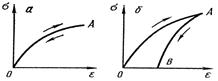
Серпімді емес материал үшін күшті түсіру (ОА қисық сызығы) мен күштен босату (АВ қисық сызығы) заңдары әр түрлі (12.1, б сурет). Күштен толық босатқан кезде денеде қалдық илемді деформация бар болады.
Көлемдік кернеу күйіне өте отырып кернеу мен деформация арасында сызықты емес изотропты байланысты орнату үшін оқулық [1, 4] келтірілген теңдеулерді қолданайық. Нәтижесінде Гук заңын қорытындылайтын мынандай байланыстарды аламыз.
σо = k Δ; (12.6)
D σ = 2 μ (Г) D ε. (12.7)
Мұндағы k = const, ал μ (Г) функциясы өзгермелі ығысу модулі болып саналады. Әрі оқулық [1, 4] келтірілген формуладан мынандай күйдің механикалық теңдеуі келіп шығады:
Т = μ (Г) Г. (12.8)
Нақты материалдар үшін мынандай орнықтылық шарты орындалады: d Т /d Г > 0.
Сөйтіп, бұрынғысынша сызықты емес-серпімді орта үшін кернеу мен деформация арасында бір қатарлы байланыс бар деп есептейміз. Осы байланыста орташа кернеу мен көлемнің салыстырмалы өзгеруі арасында, ал тағы да D σ және D ε девиаторлары арасында пропорциональды байланыс бар болды. Бірақта соңғы байланыс сызықты емес түрді алады және (12.8) күй теңдеуімен анықталады.
Сызықты-тұтқырлы орта. Сызықты-тұтқырлы ортаны зерттеуге өте отырып орташа кернеу σо деформация жылдамдығынан тікелей тәуелді емес қысымнан (- р) және көлемдік деформацияның жылдамдығына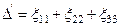 
пропорциональды қосымша кернеуден 
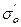тұрады деп былай болжайық:
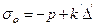. (12.9)
Оқулық [1, 4] келтірілген байланысты пайдалана отырып және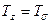 
, ал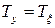 
болсын дегенді негізге алып Ньютонның гипотезасын қорытындылайтын мынандай теңдеуді аламыз:
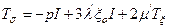. (12.10)
Осы теңдеу скалярлық түрде былай жазылады:
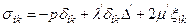. (12.11)
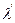және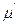 
коэффициентерін тұтқырлық коэффициентері деп атайды. Бұл коэффициентер деформация және деформация жылдамдығынан тәуелді болмағандығынан тұтқырлық тұрақтысы деп аталады. Бірақта осы коэффициентер температурадан тәуелді болуы мүмкін.
Жоғарыда жазылған теңдеулерді жазудың басқаша түрі мынандай:
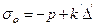; (12.12)
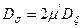. (12.13)
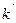тұрақтысын көлемдік тұтқырлықтың коэффициенті деп атайды.
Егер орта қысылмайтын болса, онда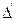 
= 0 және (12.12), (12.13) теңдіктері кернеу және жылдамдық девиаторларының пропорциональдық жағдайына келтірілінеді.
Соңында, егер тұтқырлық коэффициентері 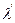және 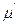нөльге тең болса, онда мынаны аламыз: 
, (12.14)
яғни кернеу тензоры шар тензорымен сәйкес келеді, ал кернеу девиаторы нөльге тең болады. Осы өте оңды сұйықтың негізгі қасиеті.
Сызықты емес-тұтқыр орта. Енді кернеу мен деформация жылдамдықтары арасындағы сызықты емес изотропты байланысты қарайық. Сызықты тұтқырлықтың заңдарын қорытындылайтын байланыстарда мынандай түр бар:
; (12.15)
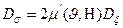. (12.16)
мұндағы k ' = const, ал μ '(J, Н) функциясы өзгермелі ығысу модулі болып саналады. Соңғы коэффициент температурадан және ығысу деформациясы жылдамдығы қарқындылығынан тәулді болады.
Сызықты емес-тұтқырлы орта күйлерінің механикалық теңдеуінде келесі түр бар болады: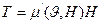 
. (12.17)
Илемділік
Изотропты орта үшін илемділіктің басталуының шарты. Күрделі кернеу күйі жағдайы үшін өте жақсы серпімді-илемді ортаның моделін қорытындылайық. Бір осьті кернеу күйі жағдайында металдың илемділік күйге өтуі ағым шегіне жеткен кезде жүретіндігін біз анықтадық.
Жалпы жағдайда илемділік шарты (жиі тағы да ағым шарты деп аталады) мынандай түрде жазылады: f (σik) = k, k = const, (12.18)
мұндағы σik – кернеу тензорының сыңарлары; k – ағым шегімен байланысты материалдың константасы.
Сонда, дене әлі серпімділік күйде болған кезде мынандай теңсіздік орындалатынын болжайды: f (σik) < k, (12.19)
ал илемділік күйге өту (12.18) шартына сәйкес келеді.
Ең үлкен жанама кернеулердің тұрақтылық шартты. Осы шарт (Треска-Сен-Венан шарты) келесі түрде жазылады:
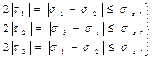(12.20)
Мұндағы τ1, τ2, τ3 – басты аудандарға π/4 бұрышымен еңкейген алаңдарда әсер ететін ең үлкен жанама кернеулер.
Жоғарыда біз айтқанымыздай σ1 ≥ σ2 ≥ σ3 шартының орындалуы талап етілмейді.
Серпімділік күйде (12.20) барлық шарттар теңсіздік белгісімен орындалады. Илемділік күйде бір немесе екі шартта теңдік белгісі болуы қажет. Осы кезде, бар болатын ең үлкен жанама кернеулер тұрақты мәнді сақтайды.
σ1 = τs, σ2 = 0, σ3 = -τs болған кезде пайда болатын таза ығысудағы ағым шегін τs деп белгілейік. (12.20) формуласынан, созған кездегі ағым шегі (σs) τs-пен мынандай тәуелділікпен: σs = 2 τs байланысты екендігі шығады.
Треска-Сен-Венан илемділік шартты басты кернеулер кеңістігінде кординатты осьтерге бірдей еңкейтілген алты қырлы призмамен көрсетіледі (оқулық [4] қараңыз). Девиаторлы жазықтықпен призманың қилысуы болып келетін илемділік шартты дұрыс алты бұрыш болып саналады.
Ең үлкен жанама кернеу ең үлкен және ең кіші басты кернеулердің жыртылай айырмасына тең болатындықтан аралық басты кернеу илемділік шартына әсер етпейді.
Жанама кернеу қарқындылығының тұрақтылық шарты. Алты қырлы призманы, оның айналасында сызылған дөңгелек цилиндрмен айырбастап мынандай Губер-Мизес илемділік шартына келеміз: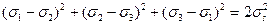 
. (12.21)
Девиаторлы жазықтықпен цилиндрдің қилысуы болып келетін илемділік шартты дұрыс алты қырлының айналасында сызылған шеңбер болып саналады (оқулық [4] қараңыз). Жанама кернеудің қарқындылығы мынаған тең болғандықтан:
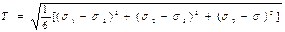, (12.22)
Губер-Мизес илемділік шартын мынандай түрде жазуға болады: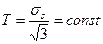 
, (12.23)
яғни осы шарт жанама кернеу қарқындылығы тұрақты болып келетін шарт болып сананалады.
Үлгілікті созған кездегі ағым шегімен таза ығысу кезіндегі ағым шегін былай салыстырайық:
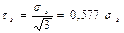. (12.24)
Жазық кернеу күйі. Жоғарыда жазылған илемділік шартын жазық кернеу күйі жағдайы үшін қарайық (σ3 = 0). Треск-Сен-Венан шарты мынандай түрде жазылады:
σ1σ2 > 0 және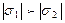 
болған кезде 
;
σ1σ2 > 0 және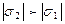 
болған кезде 
;
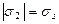σ1σ2 < 0 болған кезде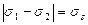 
.
Осы формулалар σ1σ2 координат жүйесінде координатты осьті ағым шегіне σs тең кесіндінімен қиып өтетін АВСДЕF алты бұрышты жазықтықты анықтайды (оқулық [4] қараңыз).
Губер-Мизес шарты σ3 = 0 болған кезде мынандай түрді қабылдайды:
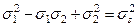(12.25)
және алты бұрыштының айналасында сызылған эллипстің теңдеуі болып саналады.
Созатын күшпен, ішкі қысыммен және бұрау моментімен жұқа қалыңдықты цилиндрлі құбырларды сынап тәжірибелерді жүргізгенде (біркелкі жазық кернеу күйіне жақын жағдайда) Рош пен Эйхингер, А.М. Жуков және басқа зерттеушілер тәжірибелік зерттеулердің нәтижесі Губер-Мизес илемділік шартымен жақсы сәйкес келетіндігін дәлелдеді (оқулық [4] қараңыз). Сондықтан илемділік теориясын тұрғызған кезде Губер-Мизес илемділік шарты негізгі ретінде қабылданды.
«Бірлік қисық сызығы» гипотезасы. Деформацияны кішкентай деп есептеп q параметрі ретінде ығысу деформациясының қарқындылығын Г таңдайық. Осы кезде d Г /d t ≥ 0 екендігін жоромолдайық. Күйдің механикалық теңдеуін былай жазуға болады:
T = T (J, Г) = μ (J, Г) Г, (12.26)
мұндағы μ – температураның және ығысу деформациясы қарқындылығының кейбір функциясы.
Осымен біз мынанандай «бірлік қисық сызығы» гипотезасын қабылдадық: дененің элементіне белсенді күш түсірген кезде жанама кернеудің қарқындылығы кернеу күйінен тәуелді емес элемент температурасы мен ығысу деформациясы қарқындылығының функциясы болады.
μ (J, Г) функциясын цилиндрлік үлгілікті созу немесе бұрау тәжірибелерінен табуға болады.
Сөйтіп, созған кезде сызықты кернеу күйі сұлбасын іске асыра отырып қысылмайтын материал үшін мынаны аламыз: 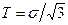, 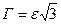. Осы теңдеулерді қолданып σ – ε қисық сызығын жеңіл Т – Г қисық сызығына қайта салуға болады.
Үлгілікті бұраған кезде таза ығысу сұлбасы іске асырылады. Сондықтан мынандай теңдеулерді қолдануға болады: T = τ, Г = γ = 2ε12.
Сыналатын үлгіліктің температурасын бір ізді түрлендіріп, тәжірибелік мәліметтерді өңдеудің математикалық теориясын қолданып және зерттеудің нәтижесін аппроксимациялап іздейтін функцияны аламыз.
Кішкентай серпімді-илемді деформацияның теориясы. Изотропты серпімді-илемді орта үшін кернеу мен кіші деформация арасында сызықты емес байланысты тапқан кезде (12.6) және (12.7) формулаларын пайдаланайық. Осы кезде изотермиялық процестерді ғана қарап мынаны жаза аламыз: σо = k Δ; (12.27)
D σ = 2μ D ε. (12.28)
Көлемнің салыстырмалы өзгеруі Δ = ε11 + ε22 + ε33 ылғида бастапқы қалпына келгіш (серпімді), ал (12.27) байланысы сызықтыққа жақын болатындығын тәжірибелер көрсетеді (бастапқы кеуектілігі бар ұнтақты және композитті материалдарды деформациялау процесі қазір қаралып жатқан жоқ).
Сонымен k = const қабылдауға болады. μ = μ (J, Г) екендігін қабылдап және осымен «бірлік қисық сызығы» гипотезасын қабылдап илемділік деформациясы процестерін бейнелеуге мүмкіндік аламыз. Сонда кішкентай серпімді-илемді деформациясы теориясының келесі бастапқы ережесін тұжырымдауға болады:
1. Орта изотропты.
2. Орташа кернеу серпімді түрі бар салыстырмалы көлемнің өзгеруіне пропорциональды.
3. Кернеу мен деформация девиаторлары пропорциональды.
Үшінші ереженің нәтижесі болып кернеу мен деформация тензорларының басты осьтерінің сәйкес келуі және девиаторлардың басты мәндерінің пропорциональдығы саналады.
Жеке жағдайларды қарайық. Оларға мыналар жатады:
сызықты серпімді күй: μ = const;
өте жақсы илемділік күй: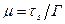 
, сонда 
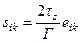; (12.29)
деформациялық беріктенген күй: T = μ (J, Г) Г және 
= 2 μ (J, Г)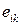 
,
немесе 
; (12.30)
серпімді күштен босату күйі:
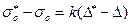; (12.31)
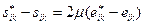, μ = const. (12.32)
Күштен босатудың басына сәйкес келетін кернеулер мен деформацияланған күй жұлдызшамен белгіленген.
Егер температуралық өріс стационарлы болмаса, онда (12.27) теңдеуін келесі түрде жазу қажет: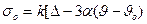 
(12.33)
мұндағы a − температуралық ұлғаюдың коэффициенті; J о – бастапқы температура.
T = μ (J, Г) Г функциясы T, Г, J кеңістігінде кейбір бетті бейнелейді (оқулық [4] қараңыз). Серпімді деформация аймағында T ≤ τs(J) осы бет сызықты бетке T = μ (J) Г ауысады, мұндағы μ (J) – температурадан тәуелді болатын ығысу модулі.
Кішкене серпімді-илемді деформациясының теориясы қарапайымға жақын күш түсірген кезде және монотонды температураны өзгерткен кезде тәжірибелік мәліметтермен жақсы дәлелденген. Қарапайым деп күш түсіргенде дененің барлық нүктелерінде кернеу тензорының сыңарлары кейбір параметрге пропорциональды өсетін күш түсіруді айтады. Олай болмайтын болса, онда күш түсіруді күрделі деп айтады. Күрделі күш түсіру үшін жақсы нәтижені тұтқырлы-илемді ағыс теориясы береді.
Тұтқыр-илемді ағыстың теориясы. Кернеу кеңістігінде П 9 дене элементінің деформация жылдамдығы жоғарлаған сайын біркелкі ұлғайатын ағым бетін ∑ салайық («ыстық» деформациялау). Осыдан кейін бет теңдеуін келесі түрде жазайық:
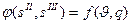, (12.34)
мұндағы f − J = const болған кезде деформациялау жылдамдығын сипаттайтын кейбір параметрдің q өсетін функциясы.
Кернеу девиаторының үшінші инвариантының әсерін ескермей q параметрі ретінде ығысу деформациясы жылдамдығының қарқындылығын Н таңдап (12.34) теңдеуін орта күйінің механикалық теңдеуі түрінде былай жазайық:
T = g (J, H) H, (12.35)
Соңғы теңдеуді жазған кезде келесі ғылымдық болжамды қабылдайық: илемді ағыс кезінде жанама кернеудің қарқындылығы кернеу күйінен тәуелді емес температура мен ығысу деформациясы жылдамдығы қарқындылығының функциясы болады.
Осы сызықты емес-тұтқыр ортаның теориясы аппараты көмегімен қыздырылған металдың тұтқыр беріктенуін жазуға мүмкіндік береді.
Серпімділік деформация және температуралық кернеуді илемділік деформациямен салыстырғанда аз деп қабылдап, оларды ескермейік. Осыдан кейін илемділіктің деформациялық теориясы сызықты емес серпімділік теориясын жинақтап қорытындылағандай сызықты емес тұтқырлық теориясын жинақтап қорытындылайтын тұтқыр-илемді ортаның ағыс теориясын негізгі ережелерін тұжырымдауға болады:
1. Орта изотропты және қысылмайды.
2. Кернеу мен деформация жылдамдығы девиаторлары пропорциональды:
D σ = 2 gD ξ. (12.36)
Осыдан кернеу мен деформация жылдамдығы тензорларының басты осьтері сәйкес келетіндігі, ал сәйкесті девиаторлардың басты мәндері пропорциональды болатындығы шығады.
(12.35) теңдеуінің жеке жағдайларды қарайық. Оларға мыналар жатады:
сызықты тұтқырлы күй: g = const;
өте жақсы илемділік күй: 
, сонда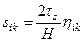 
; (12.37)
тұтқырлы беріктенген күй: T = Т (J, H) = g (J, Н) Н және = 2 g (J, Н)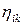 
, немесе
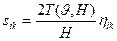. (12.38)
Илемділік теориясының жеке вариантары: А. А. Ильюшиннің теориясынан жеке варианттар ретінде жоғарыда тұжырымдалған илемділік теориясы шығады. Осы теорияларға мыналар жатады:
Деформациялық илемділік теориясы. Жалпы теория шеңберінде қарапайым деформация процестеріне осы теорияны қолдануға болады.
Деформациялық илемділік теориясы изотроптылық постулатынан тікелей шығады. Белсенді күш түсіру процестері үшін осы теория мынандай қатнастармен көрсетіледі:
кернеу мен деформация девиаторларының пропорциональдылығы
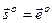; (12.39)
«бірлік қисық сызығы» гипотезасы
T = μ (J, Г) Г; (12.40)
шарлық тензорлардың пропорциональдылығы
; (12.41)
немесе скалярлық түрде
= 2 μ (J, Г) 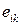, (12.42)
Күштен босатқан кезде Гуктың қорытылған заңын қолданады. Изотермиялық емес процестер үшін температурадан тәуелділік t бойынша функционалды өзгешілікке алып келеді. Бірақта сараптамада әдетте (12.40) аяққы тәуелділігін қолданады.
Тұтқыр-илемді ағым теориясы. Осы теория А. А. Ильюшиннің теориясы шеңберінде аз қисықтықты процестер теориясы болып есептеледі. Тұтқыр-илемді ағым теориясы келесі тәуелділіктерді жазуға мүмкіндік береді:
кернеу мен деформация жылдамдығы девиаторларының пропорциональдылығы
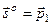; (12.43)
деформациялық және жылдамдықтық беріктенуді ескерген «бірлік қисық сызығы» гипотезасы T = g (J, Λ, Н) Н; (12.44)
кернеу мен деформацияның шарлық тензорларының пропорциональдылығы
; (12.45)
Кысылмайтын материал үшін осы қатнас скалярлық түрде мынандай түрде жазылады:
= 2 g (J, Λ, Н)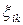 
, (12.46)
Металдарды қысыммен өңдеудің процестерін есептеген кезде айтылған теорияларды қолданудың мүмкіндігін, осы процестерде дененің барлық нүктесінде сараптамалық аз қисықтықты траектория іске асыратылатын жағдаймен дәлелдейді. Осы үшін сыртқы күштің байсалды өзгеруі жеткілікті, яғни кешігу ізі ретіндегі процесс ұзындығында түзу сызықтан сыртқы күштің траекториясының ауытқуы (сәйкесті кеңістікте), осы траекторияның болып өткен бөлімінің ұзындығынан кіші болуы қажет.
Монотонды аяққы деформациялар. Дәлме-дәл айтқанда жоғарыда қаралған А. А. Ильюшин теориясы кішкентай деформацияларға әділетті болғанына қарамай, оны аяққы илемді деформацияның теориясын дәлелдегенде негіз болатын тория ретінде қабылдауға болады. Аяққы илемді деформацияның теориясы металдарды қысыммен өңдеу процестерін бейнеленген кезде кеңінен қолданатыны белгілі. Сонда екі әр түрлі ғылымдық бағытпен жүруге болады.
Біріншісі Г. А. Смирнов-Аляев, В. М. Розенберг және олардың қызметтестерінің еңбектерінде дамытылған бағыт болып саналады. Осы бағыт кіші серпімді-илемді деформацияның деформациялық теориясын қорытындылайды.
Егер логарифмдық деформация тензорының басты осьтерінде орналасқан барлық материальды бөлшектер, элементарлы материальды көлемнің пішін өзгертуінің барлық болып өткен процестерінде осы осьтерде орналасқан болса, онда анықтама бойынша элементарлы материальды көлемнің деформациясы монотонды деп аталады. Бірақта осы осьтер байқаушының координат жүйесіне қатысты өзінің бағытын өзгертуіде мүмкін.
Осымен бірге, элементарлы материальды көлемнің деформациясы монотонды болуы үшін Лоде параметрі
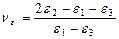(12.47)
берілген материльды көлемнің пішін өзгерту процесінде өзгермейтін болып қалуы қажет етіледі. Осы шарттардың біреуі ғана сақталмаған жағдайда деформация монотонды емес болып саналады.
Монотонды деформацияның мысалы болып түзубұрышты параллелепипедтің біркелкі деформациясы саналады. Осы жағдай үшін логарифмдік деформация шексіз кішкентай деформацияларды қосудың нәтижесі болатындығын біз жоғарыда көрсеттік. Осымен байланысты логарифмдік деформацияны жиі дәл деформация деп атайды.
Осыған ұқсас түрде, еркін элементарлы көлемнің монотонды деформацияларынан пайда болған логарифмдік деформацияларды пішін өзгертудің жеке кезеңдеріне сәйкес келетін шексіз кішкентай басты деформацияның қосындысы ғып санауға болатындығы дәлелденген. Осындай логарифмдік деформацияның уақыт бойынша туындасы деформация жылдамдығы тензорының басты сыңарларына тең, ал ығысу деформациясының қарқындылығы
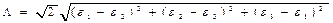(12.48)
мынандай формаламен анықталатын: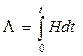 
ығысу деформациясының дәрежесімен сәйкес келеді. Мұнда уақыт бойынша интегралдау көлем элементінің қозғалу траекториясының бойымен орындалады.
Кішкентай серпімді-илемді деформацияның (12.27), (12.28) қатнастарын жазып және шексіз кішкентай деформацияларды қосуды орындап, монотонды деформациялаған кездегі аяққы деформация теорисының теңдеулеріне келеміз. Осындайда теорияның негізгі ережелері келесідей болады:
1. Орта изотропты.
2. Орташа кернеу серпімді түрі бар көлемнің салыстырмалы өзгеруіне пропорциональды, яғни
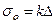, k = const. (12.49)
3. Кернеу девиаторы және логарифмдік деформацияның девиаторы пропорциональды, яғни
. (12.50)
Материалдың нақты қасиеті «бірлік қисық сызығы» гипотезасы шеңберінде мынандай тәуелділікпен бейнеленеді:
μ = μ (J, Λ). (12.51)
Соның ішінде, сызықты серпімді күй үшін мына теңдікті жазған дұрыс: μ = const.
Нақты илемді күй үшін теңдеуді мынандай түрде жазады: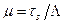 
, және де
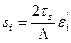, (12.52)
мұндағы 
− логарифімдік деформациясы девиаторының сыңарлары; si – кернеу девиаторының басты сыңарлары.
Деформациялық беріктенген кезде мынаны жазуға болады:
Т = μ (J, Λ)Λ (12.53)
және
si = 2 μ (J, Λ)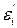 
. (12.54)
Мұралық беріктенетін ортаның тұтқырлы-илемді ағыс теориясы. Металдарды қысыммен өңдеген кезде денені монотонды деформациялаудың мүмкіншілігі бүгінгі күнге дейін толық дәлелденбеген. Сірә, дененің ең кернеулі бөлімдерінің деформациясын жуықты түрде монотонды деп санауға болатын процестердің кейбір кластарын бөлуге болады. Тым жалпы жағдайдағы металдар мен қорытпалардың аяққы пішін өзгертуінің шеттік есебін шешкен кезде, соңғы жылдары тұтқыр-илемді ағыс теориясын қорытындылайтын теория кеңінен қолданылып келеді. Осы теорияда тұтқыр және деформациялық беріктену, температураның біркелкі таралмауының әсері, материалдың мұралық қасиеті ескеріледі. Ұнтақты материалдарды деформациялау процесін талдаған кезде көлемнің кері айналмайтын илемді өзгеруін ескереді. Осы кезде мөлшері бойынша илемді деформациямен салыстырғанда өте кішкентай деп серпімді деформацияны ескермейді.
Дененің бастапқы күйін деформацияланбаған, ал бастапқы кернеуін нөльге тең деп санап, байқаушының физикалық үш өлшемді кеңістігінде кейбір траектория бойымен элементарлы материальды көлемнің қозғалысын қарайық.
Деформациялаудың тарихын бейнелеген кезде тәуелді емес параметр ретінде t уақытын және осы уақытпен бір қатарлы байланысқан кейбір параметр λ (мысалы, ығысу деформациясының дәрежесі Λ) алайық.
t уақытысындағы көлемнің салыстырмалы өзгеруін былай есептейік:
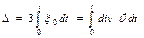. (12.55)
Тығыз байланыс теңдеуін қолдана отырып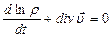 
, Δ мөлшерін тығыздықтың өзгеруімен былай байланыстырайық: 
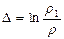, (12.56)
мұндағы ρ 1 – бөлінген элементің бастапқы тығыздығы.
Осаған ұқсас уақыт бойынша траекторияның бойымен интегралдаумен ығысу деформациясының дәрежесі былай табылады: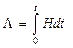 
.
Δ және Λ мөлшерлері анықтаушы теңдеулерді жазған кезде қолданылатын болады.
Мұралық беріктенетін ортаның тұтқырлы-илемді ағыс теориясының негізгі ережелерін келесі түрде тұжырымдайық:
1. Орта изотропты;
2. Орташа кернеу көлемнің салыстырмалы өзгеруіне пропорциональды, яғни
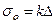; (12.5
