1. На новой странице в тетради по выполнению практических занятий запишите число. Опустившись ниже на 1см, запишите номер и тему практического занятия: « Интегрирование заменой переменной и по частям в неопределённом интеграле».
2. Под темой практического занятия запишите номер варианта.
3.Далее записывайте номер задания, перепишите текст задания.
4.С новой строчки запишите решение и ответ (см. образец отчета по практическому занятию).
Образец отчета по практическому занятию №1
1. Найти интегралы по формуле интегрирования по частям:
а ) 
.
Решение. Пусть 
, тогда 
.
Ответ: 
.
б) 
.
Решение. Пусть 
, тогда 
.
Ответ: 
.
в) 
Решение. Пусть 
, тогда 
.
Ответ: 
г) 
.
Решение. Пусть 
, тогда 
.
Ответ: 
.
2. Найти интегралы следующих тригонометрических функций:
а) 
.
Решение. Преобразуем подынтегральное выражение с помощью формулы 
: 
, тогда
Ответ: 
б)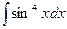 
.
Решение. Здесь 
. Преобразуя подынтегральную функцию с помощью соответствующих формул, находим
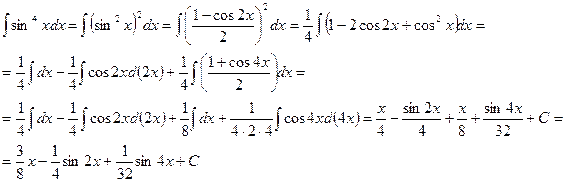
Ответ: 
в)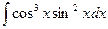 
.
Решение. В данном случае 
. Получаем
Ответ: 
3. Найти интегралы:
а) 
.
Решение. Вычислим данный интеграл, используя метод подстановки.
Применим подстановку 
, откуда 
и 
.
Ответ: 
б) 
.
Решение. Преобразуем подынтегральное выражение: выделим полный квадрат в знаменателе: 
.
Применим подстановку 
, тогда 
и 
.
Ответ: 
в) 
.
Решение. Наименьшее общее кратное степеней 2 и 4 радикалов, через которые записана подынтегральная функция, равно4. поэтому полагаем
, тогда 
, 
.
Первый и третий интегралы – табличные, а для нахождения второго интеграла воспользуемся методом подстановки.
Пусть 
, тогда 
и 
.
. 
Ответ: 
Раздел «Математическая логика»
Тема «Логика высказываний»
Практическое занятие № 2
«Решение задач на применение алгебры логики»
Учебная цель: формировать умение обосновывать истинность высказывания Учебные задачи:
1.Научиться составлять высказывания;
2.Уметь применять таблицу истинности высказываний;
3. Использовать основные равносильности для определения истинности высказываний.
Образовательные результаты, заявленные во ФГОС третьего поколения:
Студент должен
уметь:
- пользоваться таблицами, схемами при решении задач;
знать:
- способы обоснования истинности высказываний.
Задачи практической работы:
1.Повторить теоретический материал по теме практической работы.
2.Ответить на вопросы для закрепления теоретического материала.
3.Решить задачи на определение высказываний и их истинности.
4.Оформить отчет.
Обеспеченность занятия (средства обучения):
1.Учебно-методическая литература:
Математика: Учебное пособие / Под ред. С.Г.Григорьев. – М.: Издательский центр «Академия» -М, 2007. – 382 с.
2.Справочная литература: М.С. Спирина, П.А. Спирин. Дискретная математика. – М.: «Академия», 2007, Г.А. Гончарова, А.А. Мочалин. Элементы дискретной математики. – М.: ФОРУМ – ИНФРА, 2004.
3.Рабочая тетрадь: тетрадь для практических занятий в клетку.
4.Калькулятор: простой.
5. Ручка.
