1. Повторить теоретический материал по теме практического занятия.
2. Ответить на вопросы для закрепления теоретического материала.
3. Изучить методические рекомендации по выполнению практических заданий.
4. Решить ДУ.
5. Оформить отчет.
Обеспеченность занятия (средства обучения):
1. Справочная литература:
- Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних профессиональных заведений. – М.: Высшая школа, 2009. – 495 с.
- Письменный Д. Конспект лекций по высшей математике. Часть 2. – М.: Айрис-Пресс, 2009. – 256 с.
2. Рабочая тетрадь (тетрадь для практических занятий в клетку).
3. Ручка.
Краткие теоретические и учебно-методические материалы
По теме практического занятия
ДУ с разделяющимися переменными называется уравнение вида
. (2)
Вопросы для закрепления теоретического материала
1. Что такое дифференциальное уравнение?
2. Что называется решением ДУ?
3. Что такое общее решение ДУ?
4. Что такое частное решение ДУ?
5. Что такое ДУ с разделяющимися переменными?
Задания для практического занятия №2
Задание 1. Найдите общее решение ДУ.
Задание 2. Найдите частное решение уравнения, удовлетворяющее указанным начальным условиям: у и х.
Инструкция по выполнению заданий практического занятия №2
1. Изучите краткие теоретические и учебно-методические материалы по теме практического занятия.
2. Ответьте на вопросы для закрепления теоретического материала.
3. В Приложении 2 выберите свой вариант и выполните задания 1, 2.
Методика анализа результатов, полученных в ходе практического занятия
1. Общее решение ДУ. Для решения ДУ (6) нужно сначала разделить переменные: 
(ДУ с разделёнными переменными), а затем проинтегрировать обе части полученного равенства: 
.
2. Частное решение ДУ. Для того чтобы найти частное решение, необходимо сначала получить общий интеграл, а затем, подставив начальные условия, найти постоянную величину С. Далее, подставив С в общее решение, получаем частный интеграл.
Порядок выполнения отчета по практическому занятию
1. В тетради для практических занятий напишите название практического занятия и номер своего варианта.
Студенты, номер зачётной книжки которых заканчивается цифрой 1,2 выполняют вариант 1,
цифрами 3, 4 – вариант 2, цифрами 5,6-вариант 3, цифрами 7,8- вариант 4,цифрами 9,0- вариант-5.
2. Перепишите ДУ для конкретного варианта (Приложение 2).
3. Приведите ДУ к уравнению с разделёнными переменными.
4. Проинтегрируйте обе части уравнения (Таблица 1).
5. Найдите общее решение.
6. Подставив начальные условия, найдите постоянную величину С.
7. Напишите частное решение.
Образец отчета по практическому занятию
Практическое занятие №2
«ДУ первого порядка с разделяющимися переменными»
Вариант 0
Задание 1. Найдите общее решение ДУ 
.
Решение.
Сначала разделим переменные:
.
Далее проинтегрируем обе части полученного равенства:
Используя свойство логарифмов, получим:
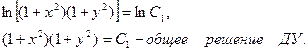
Задание 2. Найдите частное решение уравнения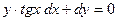 
, удовлетворяющее указанным начальным условиям: 
при 
.
Решение.
Разделим переменные: 
.
Проинтегрируем обе части полученного уравнения:
Для нахождения значения произвольной постоянной С подставим значения и в выражение для общего решения: 
или 
, откуда 
.
Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид 
.
Приложение2.
| № варианта | Задание 1 | Задание 2 | ||
| ДУ | ДУ | х | у | |
а) 
| а) 
| 
|
| |
б) 
| б) 
| 
|
| |
а) 
| а) 
|
| 
| |
б) 
| б) 
|
| 
| |
а) 
| а) 
|
| 
| |
б) 
| б)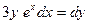 
|
|
| |
а) 
| а) 
| 
|
| |
б) 
| б)
|
| 
| |
а)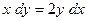 
| а) 
|
| 
| |
б) 
| б) 
|
|
|
Практическое занятие №3
«Нахождение частных производных и полного дифференциала функций»
Учебная цель: формировать умение находить частные производные и дифференциалы функций.
Учебные задачи:
1) научиться находить частные производные по х;
2) научиться находить частные производные по у;
3) научиться находить полный дифференциал в точке.
