1. Изучите краткие теоретические и учебно-методические материалы по теме практического занятия.
2. Ответьте на вопросы для закрепления теоретического материала.
3. В Приложении 1 выберите свой вариант и выполните задания 1, 2.
Методика анализа результатов, полученных в ходе практического занятия
1. Общее решение. Проинтегрировав почленно уравнение 
, получаем: 
- его общий интеграл.
2. Частное решение ДУ. Для того чтобы найти частное решение, необходимо сначала получить общий интеграл, а затем, подставив начальные условия, найти постоянную величину С. Далее, подставив С в общее решение, получаем частный интеграл.
Порядок выполнения отчета по практическому занятию
1. В тетради для практических занятий напишите название практического занятия и номер своего варианта.
Студенты, номер зачётной книжки которых заканчивается цифрой 1,2 выполняют вариант 1,
цифрами 3, 4 – вариант 2, цифрами 5,6-вариант 3, цифрами 7,8- вариант 4,цифрами 9,0- вариант-5.
2. Перепишите ДУ для конкретного варианта (Приложение 1)
3. Проинтегрируйте обе части уравнения (Таблица 1).
4. Найдите общее решение.
5. Подставив начальные условия, найдите постоянную величину С.
6. Напишите частное решение.
Образец отчета по практическому занятию
Практическое занятие № 1 «ДУ первого порядка с разделенными переменными»
Вариант 0
Задание 1. Найдите общее решение ДУ 
Имеем ДУ вида (5.2). Проинтегрируем обе части уравнения:
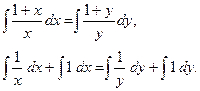
Найдём интегралы функций:
,
.
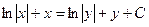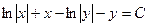Используя свойство логарифмов, получим:
- общее решение ДУ.
Задание 2. Найдите частное решение уравнения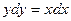 
, удовлетворяющее указанным начальным условиям: у = 4 при х = -2.
Имеем ДУ вида (5.2)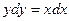 
.
Проинтегрируем обе части уравнения:
.
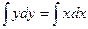Получаем общее решение ДУ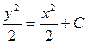 
.
Подставляя начальные условия получим:
,
.
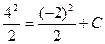Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид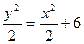 
.
Приложение1.
| № варианта | Задание 1 | Задание 2 | ||
| ДУ | ДУ | х | у | |
а) 
| а)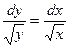 
| 
| 
| |
б)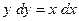 
| б)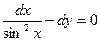 
| 
| 
| |
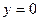
а)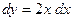 
| б) 
| 
| 
| |
б) 
| б)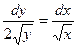 
| 
| 
| |
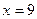
а)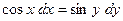 
| а)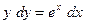 
|
|
| |
б)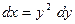 
| б) 
|
|
| |
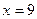
а) 
| а)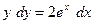 
|
|
| |
б)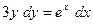 
| б)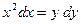 
|
| 
| |
а)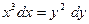 
| а)
|
|
| |
| б)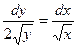
| а) 
| 
|
|
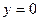
Таблица1.
Таблица интегралов
1. 
;
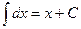2. 
;
3. 
;
4. 
;
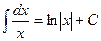5. 
;
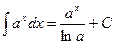6. 
;
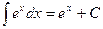7. 
;
8. 
;
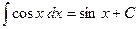9. 
;
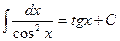10. 
;
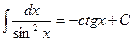11. 
;
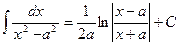12. 
;
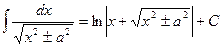13. 
;
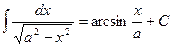14. 
.
Практическое занятие №2
«Решение дифференциальных уравнений первого порядка с разделяющимися переменными»
Учебная цель: формировать умение решать ДУ первого порядка с разделяющимися переменными.
Учебные задачи:
1) научиться находить общее решение ДУ;
2) научиться находить частное решение ДУ при начальных условиях.
Образовательные результаты, заявленные во ФГОС СПО третьего поколения
Студент должен
уметь:
- решать обыкновенные дифференциальные уравнения;
знать:
- основные понятия и методы математического анализа.
