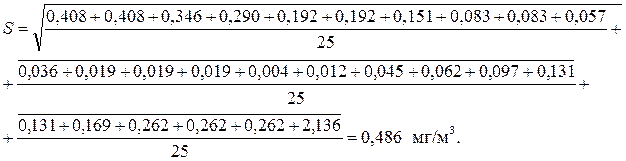Упорядочиваем совокупность результатов наблюдений и представляем в виде таблицы 2.1.
Таблица 2.1 – Упорядоченная совокупность результатов наблюдений при многократных измерениях концентраций вредных веществ в атмосферном воздухе, мг/м3 (n=26)
| № наблюдения | Исходная совокупность результатов наблюдений Хi, мг/м3 | Упорядоченные значения результатов наблюдений, мг/м3 |
| 10,000 | 10,000 | |
| 10,200 | 10,000 | |
| 10,450 | 10,050 | |
| 10,200 | 10,100 | |
| 11,000 | 10,200 | |
| 10,850 | 10,200 | |
| 10,350 | 10,250 | |
| 11,150 | 10,350 | |
| 11,150 | 10,350 | |
| 10,750 | 10,400 | |
| 11,150 | 10,450 | |
| 11,000 | 10,500 | |
| 10,950 | 10,500 | |
| 10,700 | 10,500 | |
| 10,500 | 10,700 | |
| 12,100 | 10,750 | |
| 11,050 | 10,850 | |
| 10,050 | 10,900 | |
| 10,050 | 10,950 | |
| 10,400 | 11,000 | |
| 10,000 | 11,000 | |
| 10,500 | 11,050 | |
| 10,350 | 11,150 | |
| 10,900 | 11,150 | |
| 10,250 | 11,150 | |
| 10,100 | 12,100 |
Определение точечных оценок закона распределения результатов наблюдений
Требуется определить оценки результата измерения и СКО результатов наблюдений и измерений.
Будем считать, что закон распределения неизвестен. Координата центра распределения определяет положение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фундаментальным является отыскание центра по принципу симметрии, т.е. такой точки X M на оси x, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5.
В качестве оценки центра распределения может выбираться одна из следующих оценок (в зависимости от типа распределения): выборочное среднее арифметическое, медиана, центр размаха, срединный размах, среднее арифметическое 90%-ной выборки.
2.1.1 Определяем выборочное среднее арифметическое (
) [1]:
(2.1)
где X i – отдельные результаты наблюдений,
n – общее количество результатов наблюдений.
мг/м3.
2.1.2 Определяем среднее арифметическое 90 %-ной выборки (
) [1]:
(2.2)
где 2r – число не учитываемых результатов,
n – общее количество результатов наблюдений,
X i – отдельные результаты наблюдений.
Рассчитаем 5 % выборки: 
. Т.е. отбрасываем с концов вариационного ряда по одному значению: 
мг/м3, 
мг/м3:
мг/м3.
2.1.3 Определяем медиану наблюдений (
) по формуле [1]:
Медианой 
называют наблюдаемое значение Xi, которая делит вариационный ряд на две части, равные по числу вариант.
При n - чётном:
(2.3)
мг/м3.
2.1.4 Серединный размах вариационного ряда определяем по формуле [1]:
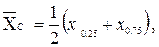(2.4)
где 
и 
− 25 % и 75 %квантили опытного распределения. Этими квантилями являются точки между 6 и 7; 19 и 20 результатами:
мг/м3,
мг/м3,
мг/м3.
2.1.5 Центр размаха определяется по формуле [1]:
(2.5)
мг/м3.
Полученные оценки центра распределения располагаем в вариационный ряд:
(мг/м3).
За оценку распределения (результата измерения) окончательно принимаем среднее арифметическое 90 %-ной выборки, так как эта оценка занимает медианное положение в ряду оценок: 
= 
= 
мг/м3.
2.1.6 Дисперсию повторяемости вычисляем по формуле (2.6):
(2.6)
