При малых объемах выборки 
для проверки согласия опытного распределения с нормальным применяется составной критерий 
Гипотеза о согласованности опытного распределения с теоретически нормальным проверяется, как показано ниже.
1.5.1 Проверка нормальности по составному критерию 
а)Проверка по критерию I
Для этого определяется значение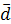 
по формуле (1.24):
(1.24)
где 
− смещённая оценка СКО результата наблюдений, найденная по формуле:
Нулевая гипотеза о принадлежности эмпирического распределения нормальному справедлива, если выполняется условие:
, (1.26)
где 
− квантили распределения 
где 
Из таблицы 7.2 [1] находим квантили распределения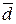 
(после интерполяции):
При n=25 
Гипотеза о нормальности распределения по критерию I, при выбранном уровне значимости подтверждается для первой выборки, т.к. условие для 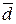выполняется:
б) Проверка по критерию II
Выполняем проверку по критерию II. Гипотеза о нормальности распределения подтверждается, если не более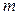 
разностей 
превзошли значения 
.
Несмещенная оценка СКО результата наблюдений (S) определяется по известной формуле:
 .
| (1.27) |
Верхняя квантиль интегральной функции нормированного распределения Лапласа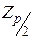 
, отвечающая вероятности 
находится по таблице 7.1 [1].
Задаются уровнем значимости 
и для известного 
из таблицы 7.3 [1] находят значения 
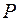и .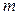
Результирующий уровень значимости составного критерия:
 .
| (1.28) | |
Если окажется, что хотя бы один из критериев не выполняется, то считают, что распределение исследуемой совокупности результатов измерений не соответствует нормальному закону.
По таблицам 7.1, 7.3 [1] находим значение m=2; Р=0,99; 
т. е., находим произведение 
и сравниваем его с максимальным отклонением. Гипотеза о нормальности распределения по критерию II справедлива, так как в выборке нет ни одной разницы, превышающей значение:
 Па <  Па.
|
Таким образом, гипотеза о нормальности закона опытного распределения по обоим критериям подтверждается при принятом уровне значимости 
.
1.5.3 Проверка нормальности распределения по критерию согласия Колмогорова А. Н.
В качестве меры расхождения между эмпирическими и теоретическими законами распределения выбрано максимальное значение D модуля разности между эмпирической функцией распределения и выбранной теоретической функцией распределения [1]:
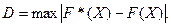(1.29)
При практическом применении критерия согласия Колмогорова А.Н. величина λ, являющаяся критериальным параметром, принимается равной:
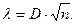(1.30)
Значение D находится после построения на одном графике эмпирической и теоретической функций изображением этих функций и представляет величину D. Затем по вычисленному значению λ по таблице (7.1) [1] определяется вероятность p (λ) как вероятность того, что за счет случайных причин максимальное расхождение между эмпирической и теоретической функциями распределения (D) будет не меньше, чем полученное из результатов измерений.
На рисунке А.7 Приложения А на одном графике показана зависимость теоретической и эмпирической функций распределения, где 
значения, полученные при построении эмпирической функции (таблица 1.9), а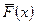 
значения, полученные при построении теоретической функции (таблица 1.9).
Таблица 1.9 – Значения теоретической и эмпирической функций распределения
| Нормированная интегральная функция F(x)=F(t) | Эмпирическая
интегральная
функция 
| 
|
| 0,0359 | 0,080 | 0,0441 |
| 0,1357 | 0,240 | 0,1043 |
| 0,3409 | 0,520 | 0,1791 |
| 0,6141 | 0,680 | 0,0659 |
| 0,8389 | 1,000 | 0,1611 |
Из данных таблицы 1.9 выбираем максимальное расхождение D:
Находим значение критериального параметра по формуле:
Производя необходимую экстраполяцию значений λ (значения взяты из таблицы 7.5 [1]), получаем вероятность p(λ):
р(λ)=0,393.
Исходя из полученных данных вероятность p (λ) не превышает критериального значения 0,8, поэтому гипотезу о соответствии опытного распределения теоретическому следует рассматривать как не правдоподобную, противоречащую опытным данным. Это означает, что принадлежность экспериментальных значений (результатов наблюдений выборки) нормальному закону не подтвердилась. Поэтому необходимо провести идентификацию формы и вида закона распределения результатов.
