Статистическая обработка результатов измерений

 

После внесения поправок на систематическую погрешность проводим статистическую обработку исправленных результатов измерений.

Определяем точечные оценки исправленных результатов измерений. Для этого по формулам, проведенным в разделе 1.1, определяем точечные оценки координаты центра распределения и СКО результатов наблюдений и измерений.

1.4.1 Статистическая обработка результатов измерений

1.4.1.1 Определяем выборочное среднее арифметическое:

 

мг/м³.

 

1.4.1.2 Определяем среднее арифметическое 90%-ной выборки ()

Среднее арифметическое находится по формуле (1.2). Пять процентов выборки в нашем случае 0,05∙n=0,05∙25=1, т.е. один результат измерения. Отбрасываем по одному измерению с концов вариационного ряда, т.е. результаты х₁=10,000 мг/м³и х₂₅=11,700 мг/м³.

 

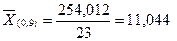мг/м³.

 

1.4.1.3 Определяем медиану наблюдений ()

При n - нечётном:

мг/м³.

1.4.1.4 Определяем центр размаха

 

мг/м³.

 

1.4.1.5 Определяем серединный размах вариационного ряда

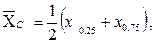
где и − 25 % и 75 %квантили опытного распределения. Этими квантилями являются точки между 6 и 7; 20 и 21 результатами:

 

,

,

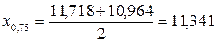мг/м³.

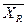
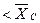
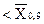
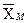
Полученные оценки центра распределения располагаем в вариационный ряд: или мг/м³.

За оценку распределения (результата измерения) окончательно принимаем среднее арифметическое 90 %-ной выборки, так как эта оценка занимает медианное положение в ряду оценок: 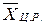= = 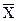11,021 мг/м³.

1.4.1.6 Дисперсию повторяемости исправленных значений результатов измерений Х_i, В вычисляем по формуле (1.18):

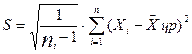, (1.18)

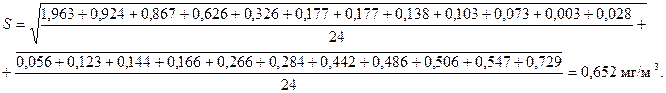1.4.2 Разделим вариационный ряд на интервалы

Число интервалов определяют, пользуясь формулой Старджесса:

 

k = 1 + 3,31∙lg n, (1.19)

 

k = 1 + 3,31∙lg 25 = 5.

 

Ширина интервала вычисляется по формуле:

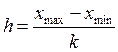, (1.20)

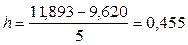мг/м³.

Определяем границы интервалов, затем определяем частоту попадания в интервалы и середины интервалов.

Результаты (после исключения грубых и систематических погрешностей, упорядочения и разбиения выборки на интервалы) представлены в таблице 1.6.

 

Таблица 1.6 – Промежуточные значения интервального ряда

 

Граница интервалов xi – xi+1, мг/м3	Середины интервалов xi0 , мг/м3	Частота попадания в интервалы mi	Статистическая вероятность (частность)
9,620-10,075	9,847		0,080
10,075-10,529	10,302		0,160
10,529-10,984	10,756		0,280
10,984-11,438	11,211		0,160
11,438-11,893	11,666		0,320
	N		1,000

1.4.5 Определение закона распределения результатов измерений

Представим заданный статистический ряд в виде гистограммы (Приложение А, рисунок А.6).

По виду гистограммы, предполагаем, что закон распределения результатов наблюдений – двумодальный.

1.4.6 Определение дифференциальной функции распределения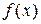

Вычислим дифференциальную функцию распределения 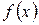для середин интервалов. Для этого вычислим значение нормированного аргумента по формуле для каждого интервала:

.

(1.21)

 

А затем, пользуясь статистической таблицей (Приложение Г) [1], определим дифференциальную функцию .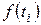

Используя свойство нормального распределения 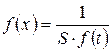, находим значения дифференциальной функции в выбранных единицах. В случае использования интервалов применяют зависимость

 

,

(1.22)

 

где – ширина интервала, в нашем случае она равна 0,450.

 

Для построения статистической функции распределения можно воспользоваться формулой для дополнительных вычислений:

.

(1.23)

 

Окончательно все вычисления сведем в таблицу 1.7.

 

Таблица 1.7 – Вероятностные параметры распределений

 

Середины интервалов xi0, мг/м3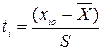
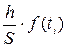
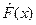
9,847	-1,801	0,790	0,551	0,0359	0,080
10,302	-1,103	0,2179	0,152	0,1357	0,240
10,756	-0,406	0,3668	0,256	0,3409	0,520
11,211	0,291	0,3825	0,267	0,6141	0,680
11,666	0,989	0,2444	0,171	0,8389	1,000

 

Для построения теоретической функции воспользуемся Приложением В [3]. Графики эмпирической и теоретической функций интегрального вида показаны в Приложении А, на рисунке А.7.

По виду статистических кривых можно также сделать заключение о нормальности распределения экспериментальных данных, хотя для окончательного заключения требуется проверка по критериям согласия (или приближенная идентификация по точечным числовым характеристикам).

Окончательно результаты по определению вероятностных характеристик первой группы наблюдений сводим в таблицу 1.8.

 

Таблица 1.8 – Параметры функций распределений первой группы наблюдений

 

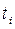
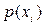
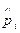
Границы интервалов xi-xi+1, мг/м3	Сере- дины интерва- лов xio, мг/м3	Нормиро-ванный параметр	Диф. функция норми- рован. нормал. распре-деления f(ti)	Диф. функция в единицах выбранной величины	Эмпири-ческая диф. функция	Эмпири-ческая инте-гральная функция	Норми- рованная инте- гральная функция F(x)=F(t)
9,620-10,0750	9,847	-1,801	0,790	0,551	0,080	0,080	0,0359
10,075-10,529	10,302	-1,103	0,2179	0,152	0,160	0,240	0,1357
10,529-10,984	10,756	-0,406	0,3668	0,256	0,280	0,520	0,3409
10,984-11,438	11,211	0,291	0,3825	0,267	0,160	0,680	0,6141
11,438-11,893	11,666	0,989	0,2444	0,171	0,320	1,000	0,8389