При равноточных измерениях за результат измерений при статистической обработке выборки, состоящей из многократных наблюдений, принимается координата центра распределения. Средневзвешенное значение центров распределений в группах принимается за результат измерений при неравноточных измерениях.
В силу конечного объёма выборки, наличия неисключенных составляющих погрешностей и различных законов распределения, результат измерения имеет неопределенность.
Зона неопределенности (доверительные границы) генерального среднего устанавливаются погрешностью результата измерения 
.
Границы могут быть заданы как симметричными, так и несимметричными, они зависят от выбранной доверительной вероятности. Чаще используются симметричные границы с двухсторонней вероятностью 
.
За погрешность результата измерения может быть принято:
а) только случайная составляющая погрешности;
б) систематическая составляющая погрешности;
в) композиция случайной и систематической составляющих погрешностей.
Характеристики погрешности измерений указываются в единицах измеряемой величины (абсолютные) и в процентах (относительные) относительно результатов измерений или истинных значений измеряемой величины.
1.7.1 Определение доверительных интервалов случайной погрешности
В случае отсутствия в результатах наблюдений систематических погрешностей или при условии, что отношение неисключенной систематической погрешности 
к оценке 
СКО результата измерения соответствует условию:
 00,
| (1.42) |
то за погрешность результата измерения принимается случайная составляющая погрешности:
 ,
| (1.43) |
где 
– коэффициент, зависящий от объема выборки, вида распределения и доверительной вероятности . В соответствии с ГОСТ 8207-76 рекомендуется устанавливать доверительную вероятность 
.
=11,400-10,050=1,350 
.
Вычисляем отношение суммарной неисключенной систематической погрешности к оценке СКО:
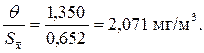
Поскольку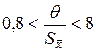 
, то погрешность результата измерения определяем как композицию случайной и систематической составляющей погрешности по формуле (9.12) [1]:
,
где 
– коэффициент, зависящий от соотношения 
.
Находим границу случайной составляющей погрешности результата измерения. Поскольку распределение случайной погрешности равномерное, то принимаем формулы:
Коэффициент определяем исходя из характера закона распределения. Для островершинных двумодальных распределений с эксцессом 
при 
с погрешностью 5 % используется формула 4.3 [1]:
 ;
|
Тогда доверительная граница погрешности результата измерения:
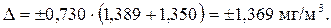
Результат измерения представляем в форме:
мг/м3; 
мг/м3;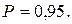 
Или 
мг/м3; 
