Основные правила вычисления пределов:
1. 
.
2. 
.
3. 
, если 
.
4. 
и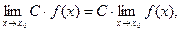 
где С = const.
5. 
.
6. 
.
Если х < х 0 и х → х 0, то употребляют запись х → х 0 – 0; если х > х 0
и х → х 0 — запись х → х 0 + 0. Числа f (x 0 – 0) и f (х 0 + 0) называются соответственно левым и правым пределом функции f (x) в точке х 0.
Функция f (x) называется бесконечно малой при х → х 0,
если 
.
Бесконечно малые функции f (x) и g (x) называются эквивалентными, если 
(обозначается f (x) ~ g (x)).
При х → 0 эквивалентными являются следующие функции:
| sin x ~ x, | tg x ~ x, | ex – 1 ~ х, | (1 + х)a – 1 ~ a · x, |
| arcsin x ~ x, | arctg x ~ x, | ln(1 + x) ~ x, ax – 1 ~ х · ln a, | 1 – сos x ~  .
|
Приведенный ряд остается справедливым, если вместо аргумента x подставить функцию 
при 
.
Рекомендации к выполнению задания
1. При вычислении пределов придерживаться следующего плана:
1) Выполнить непосредственную подстановку значения аргумента в выражение функции. Результатом этой подстановки может стать один из вариантов:
а) получен искомый предел;
б) предела функции не существует;
в) получена неопределенность.
При получении предела в пункте а) следует учесть, что
| (+¥) + (+¥) = +¥ | (+¥) · (+¥) = +¥ | (+¥) · (–¥) = –¥ |
| (–¥) + (–¥) = –¥ | (–¥) · (–¥) = +¥ | |
| С + (¥) = ¥ | С · ¥ = ¥ | (с учетом знака) |
| С – (¥) = –¥ | 
|
В пункте в) неопределенность может иметь вид: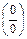 
; 
;
(¥ – ¥); (0 · ¥); (1¥); (¥0); (00).
2) В случае получения неопределенности следует провести тождественные преобразования функции, приводящие к избавлению от неопределенности. При этом используют методы:
а) выделение критических множителей;
б) применение специальных пределов;
в) использование эквивалентных бесконечно малых.
Следует отметить, что неопределенность вида (0 · ¥) с помощью тождественных преобразований приводится к виду 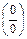или
, а неопределенность (¥ – ¥) приводится к виду (0 · ¥) вынесением общего множителя ¥–¥ = ¥ · ¥ 
или «раскрывается» приведением к общему знаменателю и использованию сопряженных выражений. Неопределенности (00), (¥0), (1¥) решают с помощью формулы 
(здесь 
принимает вид 0 · ¥).
3) При решении пределов следует знать значения:
|
|
|
пределы функций sin x, cos x, tg x и ctg х при х ® ± ¥ не существуют; так же
если а > 1
и 
если 0 < a <1;
использовать 1-й и 2-й замечательные пределы 
и 
а также равенства 
.
Пример решения задачи
Найти пределы:
1) 
2) 
.
1) Так как при подстановке х = ¥ в выражении функции получаем неопределенность , то, используя метод выделения критического множителя (им является «старшая» степень аргумента), получим:
(применяем правила 1) и 3).
2) При подставке х = 1 получим неопределенность 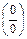. Решаем выделением критического множителя. Для того разложим на множители числитель и знаменатель. (В данном случае использование тождества а 2 – b 2 = (a – b)(a + b) и корней квадратного трехчлена.)
Условия задачи 3.
а) 
; б) 
;
а) 
; б) 
;
а) 
; б) 
;
а) 
; б) 
;
а) 
; б) 
;
а) 
; б) 
;
а) 
; б) 
;
a) 
б) 
а) 
; б) 
;
а) 
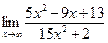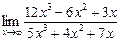; б)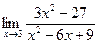 
.
Задача 4. Найти производную функции.
