Методические указания
к выполнению контрольной работы
по математике
для студентов заочной формы обучения направления
«Гостиничное дело», «Туризм»
Составитель: доцент кафедры ПМиИ, Пилосян Э.А. кафедры
Сочинского государственного университета
Рецензент:
Сочи – 2015
Порядок выполнения контрольной работы
Контрольная работа выполняется в отдельной тетради. На обложку тетради наклеивается титульный лист (см. приложение 1). Номер варианта контрольной работы совпадает с последней цифрой номера зачетной книжки студента.
Задачи решаются в том порядке, который указан в методическом пособии. Текст задачи переписывается.
Контрольная работа должна быть сдана в СГУ не позднее 15 декабря.
Если при решении задач возникают трудности, студент может обратиться за консультацией к преподавателю математики СГУ.
Задача 1. Решить систему линейных уравнений а) используя формулы Крамера; б) матричным методом (с помощью обратной матрицы).
Справочный материал к заданию
Матрицы
Матрицей 
размера m*n называется прямоугольная таблица из m строк и n столбцов, состоящая из чисел или иных математических выражений 
, называемых элементами матрицы, 
.
Суммой матриц и 
одинакового размера называется матрица 
того же размера, причем 
.
Произведением матрицы на число 
называется матрица того же размера, что и матрица , причем 
.
Произведением матриц 
и 
(размеров m*n и n*r соответственно) называется матрица размера m*r, такая что 
.
Определители второго и третьего порядков
Определитель второго порядка 
a 11 a 22 – а 12 а 21, т. е. равен разности между произведением элементов на главной диагонали и произведением элементов на побочной диагонали.
Определитель третьего порядка 
вычисляется либо через определители второго порядка разложением по элементам какой-либо строки или какого-либо столбца (например, при разложении по элементам первой строки):
,
либо по правилу треугольников: определитель равен алгебраической сумме произведений по три элемента согласно схеме:
где прямыми линиями соединены элементы определителя, произведение которых входит в сумму со своим знаком в случае А) и с противоположным знаком в случае Б), т.е.
D = а 11 а 22 а 33 + а 12 а 23 а 31 + а 13 а 21 а 32 – а 31 а 22 а 13 – а 11 а 32 а 23 – а 33 а 21 а 12.
Системой m -линейных уравнений с n неизвестными называется система вида
а 11 х 1 + а 12 х 2 + … + а 1n х n = b 1
a 21 x 1 + a 22 x 2 + … + a 2n x n = b 2
--------------------------------------
a m1 x 1 + a m2 х 2 + … + a mn x n = b m
Эту систему можно записать в матричной форме:
А · Х = В,
где
 |  |  | |||
a 11 a 12 … a 1n x 1 b 1
A = a 21 a 22 … a 2n , X = x 2, B = b 2.
----------------- --- ---
a m1 a m2 … a mn x n b m
Решением системы называется всякая матрица-столбец Х, обращающая матричное уравнение А · Х = В в тождество. Система называется совместной, если она имеет решение, и несовместной, если решений нет. Совместная система называется определенной, если решение единственное, и неопределенной, если она имеет бесчисленное множество решений.
Две системы называются равносильными, если каждое решение одной является решением другой, т.е. у них множества решений совпадают.
Если ∆ - определитель матрицы А – не равен нулю, то система совместна и определенна, ее решение задается формулой:
.
Другую форму записи этого утверждения дают формулы Крамера:
,
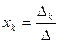где k=1,2,…,n, 
- определитель, получающийся из ∆ заменой k -го столбца на столбец свободных членов.
Пример решения задачи.
а) Решить систему уравнений по формулам Крамера:
Найдем главный определитель матрицы коэффициентов системы уравнений по правилу треугольников:
.
Так как главный определитель отличен от нуля, то решение системы существует и единственно.
Найдем определители 
, подставляя столбец свободных членов 
вместо первого, второго и третьего столбцов главного определителя соответственно:
,
,
.
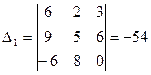Отсюда получим решение системы уравнений:
,
,
.
Ответ: (-2;1;2).
Минором 
к элементу квадратной матрицы называется определитель, составленный из элементов матрицы , оставшихся после вычеркивания i –той строки и j –го столбца.
Алгебраическим дополнением 
к элементу квадратной матрицы называется произведение 
.
б) Решить систему уравнений с помощью обратной матрицы.
Найдем матрицу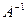 
, обратную к матрице системы 
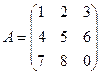методом присоединенной матрицы.
Так как определитель матрицы А равен 27 (см. предыдущий пример), то обратная матрица существует, поэтому решение системы существует и единственно.
Найдем алгебраические дополнения ко всем элементам матрицы А:
,
,
,
,
,
,
,
,
.
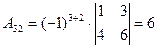Запишем присоединенную матрицу:
.
Найдем обратную матрицу:
.
Найдем решение системы уравнений:
.
Ответ: (-2;1;2).
Условия задачи 1.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
.
Задача 2. Даны координаты вершин пирамиды А 1 А 2 А 3 А 4.
Найти:
1) длину ребра А 1 А 2;
2) угол между ребрами А 1 А 2 и А 1 А 4;
3) проекцию ребра A 1 A 3 на ребро А 1 А 2;
4) площадь грани А 1 А 2 А 3;
5) длину высоты грани А 1 А 2 А 3, опущенной из вершины А 3 на ребро А 1 А 2
6) объем пирамиды А 1 А 2 А 3 А 4;
7) канонические уравнения прямой А 1 А 3;
8) общее уравнение плоскости А 1 А 2 А 3;
9) угол между ребром А 1 А 4 и гранью А 1 А 2 А 3;
10) канонические уравнения высоты, опущенной из вершины А 4 на грань А 1 А 2 А 3, и длину этой высоты.
