При отборе тех или иных методов социально-экономического исследования необходимо иметь в виду, что массовость опроса не является гарантией достоверности и надёжности результатов. Гораздо эффективнее использовать более точный инструментарий, требующий квалифицированной работы интервьюеров, статистиков, вычислителей и аналитиков, нежели проводить многотысячные опросы, которые в силу профессиональной слабости не могут дать новой информации о состоянии общественного мнения.
Методы анализа материала в социологических исследованиях в принципе не отличаются от принятых в статистике. Предварительным условием надёжности сложных видов анализа является получение общей картины простых распределений ответов на заданные вопросы, группировки по наиболее важным признакам, вычисление средних величин и анализ отклонений от средних в ту или другую сторону. При изучении силы влияния тех или иных факторов на изучаемые процессы необходимо различать факторы общего характера, в равной мере действующие на всю совокупность обследуемых объектов, и факторы специфические.
Собранная информация в процессе научного исследования подвергается тщательной обработке. Обработке подлежит весь собранный материал от первой до последней страницы, - это и есть первичная сплошная обработка материала. Она должна предшествовать написанию текста. С ее помощью можно представить общую картину всей работы, создавая тем самым благоприятные условия для написания текста на высоком научном уровне.
Этот важный этап научно-исследовательской работы состоит из нескольких стадий:
1) систематизация материала;
2) оценка пригодности информации;
3) проверка достоверности и значимости информации;
4) сопоставление информации;
5) построение предварительных и окончательных выводов.
Сначала следует систематизировать собранную информацию, то есть упорядочить разрозненные факты, создать их стройную систему согласно цели исследования. Методическими приемами систематизации является классификация и типология. Классификация - это группирование фактов в совокупности по количественным признакам, а типология - по качественным признакам. В процессе сбора информации тоже следует постоянно осуществлять ее систематизацию, то есть всегда перечитывать и раскладывать материал в соответствии с планом разработки темы. При этом по мере поступления информации, она должна находить свое место в определенном параграфе работы.
Первичная информация экономического характера после сплошной обработки подлежит статистической или вторичной обработке. Сущность этой обработки заключается в составлении таблиц, рядов, схем, графиков (кривых, диаграмм, картограмм), расчета средних и относительных величин, показателей вариации и дисперсии, корреляционных связей при факторном анализе. Таким образом, создается новая информация.
Вся собранная и систематизированная информация должна проверяться на ее достоверность и значимость. Оценка достоверности информации - особенно ответственная стадия ее обработки, которая требует высокой квалификации исследователя. Одним из способов определения достоверности собранной информации является ее математическая оценка, которая может ограничиваться выборочной проверкой ответственных элементов - методик, формул, логических рассуждений. Всю недостаточно достоверную информацию следует изъять.
Основным методом построения научных выводов в процессе обработки информации является сопоставление данных. Для получения достоверных научных выводов следует максимально сосредотачиваться на исследуемой теме и привлекать максимальное количество фактов и идей, быть любознательным и заинтересованным, эффективно использовать результаты коллективного обсуждения собранной информации.
В конце исследователь на основании предварительных выводов, которые часто значительно расширяют источники информации или, наоборот, отсекают ненужные данные, подводит итог работы и формулирует окончательные выводы. Их рекомендуется формулировать тщательно, точно, не перегружая обоснование цифровыми данными. Окончательные выводы должны быть краткими и содержательными. С их помощью читатель должен легко оценить работу, исследователь - еще раз ее проверить.
Цель эксперимента - получить некоторую числовую величину. Часто ее получают путем вычислений. Вычисление нужно проводить аккуратно и последовательно. Записи следует делать так, чтобы было много свободного места.
При вычислениях очень удобно свести числовые данные в таблицу. Очень часто числа одного столбца образуются в результате арифметических действий над числами другого или нескольких других столбцов, поэтому в начале каждого столбца следует указать вид выполняемого действия, а столбцы можно обозначить буквами в алфавитном порядке. Такая таблица позволяет облегчить расчеты и систематизировать результаты.
Необходимой частью вычисления является проверка. Нужно помнить, что ошибка в вычислении - главная причина затрат времени.
При обработке результатов измерений и вычислений необходимо соблюдать правила работы со значащими цифрами. Значащими цифрами в числах принято называть все цифры 1, 2, 3,... 9, а также нуль, но только в тех случаях, если он находится внутри или в конце числа. Так, в дробях 1,017; 0,17; 0,017 и 0,0017 первый из них имеет четыре значащие цифры, а три последних - по две значащих цифры.
Число, которым выражают результат измерения, должно характеризовать не только численное значение результата, но и точность метода. Для этого в результате нужно писать столько значащих цифр, чтобы предпоследняя цифра была достоверной. Например, есть разница между величиной навески 0,1000 г и 0,10 г. Первое число означает, что навеску (одну десятую грамма) взвешивали на аналитических весах с точностью до одной десятитысячной грамма, а второе число означает, что ту же навеску взвешивали на технических весах с точностью до одной сотой грамма.
Следует помнить, что большое количество значащих цифр характеризует не точность результатов, а лишь неумение исполнителя обращаться с результатами измерений.
При математических операциях с величинами, которые измеряются с разной точностью, необходимо придерживаться таких правил:
1. Число знаков в полученном результате, должно
указывать на точность измерения, причем предпоследний знак должен быть точным, а последний - приближенным.
Например, в результате наблюдений определено среднее значение плотности: ρ - 0,9345 г/см, квадратичная ошибка которого составляет 0,0024. Итак, третья цифра является приближенной, и ответ должен быть: ρ = 0,935 ± 0,002 г/см3.
2. Арифметические действия над приближенными числами проводятся таким образом:
а) при сложении (и вычитании) сохраняют после запятой столько значащих цифр, сколько их в числе, измеренном с наименьшей точностью;
б) при умножении и делении сохраняют столько значащих цифр, сколько их в числе, измеренном с наименьшей точностью;
в) при возведении в степень и извлечении корня сохраняют в
результате вычисления столько значащих цифр, сколько их в
числе, которое возводится в степень, или под корнем;
г) при логарифмировании в результате вычисления сохраняют в мантиссе столько значащих цифр, сколько их в числе, которое
логарифмируется.
Например, при сложении чисел 0,284; 25,86 и 3,5894 необходимо оставить в каждом числе два знака после запятой:
0,28 + 25,86 + 3,59 = 29,73.
3. При округлении приближенных чисел или результатов действий над ними различают два случая:
а) если отбрасываемая цифра меньше 5, то предыдущая цифра
не изменяется;
б) если отбрасываемая цифра равняется или больше 5, то
цифру, которая остается в результате, увеличивают на
единицу.
4. При записях результатов необходимо следить за тем, чтобы все числовые значения имели одинаковое количество значащих цифр.
Например: 2,05; 2,06; 2,10; 2 (неправильно); 2,00; 2,3 (неправильно); 2,30; 2,411 (неправильно); 2,41.
Значительное место в научном обобщении фактов, выяснении закономерностей, систематизации влияния разного рода факторов отводится таблично-графическим методам. Эти методы существенно повышают эффективность работы как с фактическим материалом, так и теоретическими схемами.
Сущность табличного метода состоит в систематизации и наглядном представлении текстовой и цифровой информации, полученной вследствие сбора данных, группирования, проведения анализа, синтеза новых показателей, прогнозирования развития событий и моделирования ситуации, в виде таблиц.
Таблица - это форма рационального изложения информации. Макет таблицы - это определенным образом структурированная система строк и столбцов, предназначенная для информационного наполнения.
Обычно таблица имеет следующее построение:

| ||||
Первым этапом заполнения макета таблицы является разработка подлежащего и сказуемого, - ключевых элементов таблицы. Подлежащее отражает объект изучения, который характеризуются определенными признаками, а сказуемое - перечень признаков, которыми характеризуется объект исследования (например, количественные показатели).
Значения одной и той же величины нужно сводить в вертикальные графы, это позволяет легко сопоставлять цифры. В заголовок граф выносят или название соответствующей величины или символ и единицу измерения. Заголовки граф должны начинаться с прописной буквы, подзаголовки - с маленькой, если они составляют одно предложение с заголовком, и с большой, если они являются самостоятельными. Высота строк должна быть не меньшей 8 мм. Графу с порядковыми номерами строк в таблицу включать не нужно.
Каждая таблица должна иметь название, которое размещают над таблицей, и печатают симметрично к тексту. Название и слово "Таблица" пишется с прописной буквы
Результаты исследования, если это возможно, нужно приводить кроме таблиц, в виде графиков, диаграмм или математических зависимостей.
Таблицы, графики и диаграммы должны быть пронумерованы, иметь названия и объяснение к обозначениям.
Например, для записи результатов наблюдений за накоплением радиоактивных изотопов в организмах подопытных животных при потреблении биологически активных добавок можно составить таблицу.
Таблица 2.1 - Динамика накопления цезия-137 в организме животных, которым вводили с пищей зародыши пшеницы (ЗП) и эламин (ЭЛ), мкг
| День наблюдения | Контроль | ЗП | ЭЛ |
| 200,6±31,1 434,8±97,3 1411,0±537,2 1761,3±484,4 2005,6±342,7 2260,9±322,1 | 190,0±35,4 352,9±114,7 824,4±312,3 1411,4±344,9 1682,1±387,2 2060,7±516,8 | 150,1±38,4 391,2±101,5 1098,1±242,8 1431,4±238,4 1624,7±255,9 1780,9±287,6 |
Порядковый номер таблицы дает возможность ссылаться на нее в тексте. Если таблица лишь одна, ее не нумеруют.
Данные, имеющие разные величины измерения, необходимо свести в отдельные графы и каждой из них дать заголовок.
Таблицу размещают после первого упоминания о ней в тексте, таким образом, чтобы ее можно было читать без поворота листа или с поворотом по часовой стрелке.
Таблицу с большим количеством строк можно переносить на следующий лист (страницу). В этом случае название таблицы не повторяют. Таблицу с большим количеством граф можно делить на части и размещать одну часть под другой в пределах одной страницы. Если строки или графы таблицы выходят за формат страницы, то в первом случае в каждой части таблицы повторяют ее головку (шапку), а во втором - боковик.
Многовековой опыт работы научных работников и практиков представлением информации в табличной форме сформировал определенные требования к составлению таблиц. К ним относятся такие:
1) размер таблицы должен быть оптимальным - слишком малая таблица будет недостаточно информативной, а большая - перегруженной данными, которые сложно анализировать;
2) все элементы таблиц - название, боковик и заголовки граф должны иметь четкие определения, трактуемые однозначно;
3) строки боковика и колонки граф должны располагаться по принципу "от общего - к частичному";
4) для облегчения работы с информацией необходимо нумеровать строки боковика и колонки граф;
5) следует использовать лишь общепризнанные (стандартные) сокращения и условные обозначения;
6) округление числовых значений по всей таблице или в пределах столбцов должны проводиться с одной степенью точности;
7) расчетные данные и показатели, полученные с использованием определенной исходной информации, обязательно отмечаются отдельно;
8) информацию о первоисточниках, на сведениях из которых построена таблица, специфику расчетов отдельных показателей, предельные коэффициенты и ограничения и т.п. располагают в примечаниях;
9) не допускается наличие в таблице незаполненных клеток;
10) названия показателей должны писаться полностью с указанием единиц измерения;
11) нужно избегать размещения в таблице разнородных показателей, в ином случае необходимо делать специальные указания на них в названиях или ссылках.
Графический метод предполагает проведение систематизации и наглядное представление информации, полученной вследствие сбора данных, группирования, проведения анализа, синтеза новых показателей, прогнозирования развития событий и моделирования ситуации, в виде графиков, диаграмм, картограмм, картодиаграмм, логических схем.
Их применение в любых исследованиях дает возможность на качественно новом уровне систематизировать накопленную информацию, лучше понять взаимосвязи, присущие предмету или явлению, улучшить возможности аналитического рассмотрения.
График - это наглядное представление количественной информации с помощью геометрических линий и фигур. Составными элементами любого графика являются: графический образ; поле графика; пространственные ориентиры; ориентиры масштаба; экспликация.
Графический образ - это основа графика. Графический образ может быть точечным, линейным, столбиковым, полосным, квадратным, круговым и фигурным (в форме рисунков или силуэтов).
Поле графика - это пространство, в котором расположены графические образы. Оно, по обыкновению, представляет прямоугольник с соотношением сторон 1:1,33 или 1:1,5).
Пространственные ориентиры - система координат или другая система символов, которая указывает на места размещения и соотношения графических образов на поле графика. Наиболее распространенные пространственные ориентиры в виде двухмерной (Декартовой) системы координат.
Результаты эксперимента откладываются на графике в виде точек, по которым проводится кривая усреднения.
Ориентиры масштаба – это шкала делений координатных осей. Экспликация – пояснения к рисунку («легенда»).
При использовании формул объяснения значений символов и числовых коэффициентов необходимо давать непосредственно под формулой и в такой последовательности, как они приведены в формуле. Значение каждого символа и числового коэффициента нужно давать с красной строки. Первую строку объяснения начинают со слова "где" без двоеточия.
Если уравнение не вмещается в одну строку, его нужно переносить после знаков равенства (=), сложения (+), вычитания (˗), точку как знак умножения заменяют знаком (×). Не допускаются переносы на знаках деления (:) и границы интервала (÷).
Выше и ниже каждой таблицы, графика (рисунка) и формулы нужно оставить не меньше одного свободной строки. Каждая таблица, каждый рисунок должны быть обсуждены, проанализированы, что именно иллюстрируют приведенные данные.
Получение точного и достоверного результата - основная задача научного эксперимента. Однако в процессе измерения невозможно получить истинное значение параметров объекта в связи с тем, что при проведении измерений на результат влияет много разнообразных факторов, в частности, объект измерения; субъект (эксперт или экспериментатор); метод и способ измерения; средство измерения; условия измерения; количество наблюдений. Многоразовое измерение одной и той же величины постоянного размера позволяет обеспечить нужную точность.
Все наблюдения и результаты опытов заносятся в рабочий
журнал. При проведении многоразовых измерений (в зависимости от необходимой точности, но не меньше трех) задача экспериментатора состоит в том, чтобы учесть и исключить из результата погрешности. Поэтому в разных областях народного хозяйства, в том числе и гостинично-ресторанном хозяйстве, полученные результаты экспериментов обрабатывают с помощью математико-статистических методов, в частности, вариационной статистики путем вычисления соответствующих характеристик.
К основным статистическим характеристикам относятся:
 – выборочная средняя величина;
– выборочная средняя величина;
S2 – выборочная дисперсия;
S – выборочное среднее квадратичное отклонение;
m – стандартная ошибка среднего (измерений);
ε – относительная ошибка среднего.
Первичная обработка результатов измерений состоит из следующих этапов:
1. Вычисление среднего арифметического значения результатов измерения по формуле:
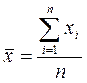 , (1)
, (1)
где  – среднее арифметическое значение;
– среднее арифметическое значение;
n – количество проведенных измерений;
хі – результат i-го измерения.
2. Вычисление среднего квадратичного отклонения по формуле:
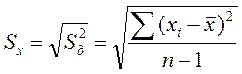 , (2)
, (2)
где Sx – среднее квадратичное отклонение;
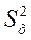 - дисперсия;
- дисперсия;
(n-1) – степень свободы.
3. Вычисление стандартной ошибки среднего по формуле:
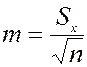 . (3)
. (3)
4. Вычисление относительной ошибки среднего по формуле:
 . (4)
. (4)
Обычно статистическую обработку результатов эксперимента рекомендуется выполнять в табличной форме:
| № измерение, і | Результат измерения, 
| 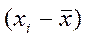
| 
|
| ... | |||
| n | |||
| ∑= | ∑= | ∑= |






