Простые механизмы. В механизме, состоящем из двух вращающихся звеньев (рис. 3.2, а, б), межосевое расстояние a = r2 ± r1 и с учетом формулы (3.4):
и 
(3.6)
(знак "+" для внешнего контакта, знак " - " для внутреннего).
Для механизмов с пересекающимися осями (рис. 3.2, в):
(3.7)
При d = d1+d2 = 900:
(3.8)
Для механизмов с перекрещивающими осями (рис. 3.2, г):
(3.9)
а) б)
в)
Рис. 3.3. Рядовые зубчатые механизмы: а) - последовательно соединенные колеса; б) - передача с паразитными колесами; в) - передача с коническими колесами
Если механизм состоит из зубчатых колес, то центроиды и аксоиды при параллельном расположении осей звеньев называются начальными окружностями и начальными цилиндрами.
Основное требование, предъявляемое к зубчатому механизму - постоянство передаточного отношения i12 в любой момент, несмотря на изменение положения точки соприкосновения контактирующих зубьев. Условие, обеспечивающее это требование, носит название основного закона зацепления; оно является следствием теоремы о соотношении скоростей в высшей кинематической паре и может быть сформулировано так: для сохранения постоянства передаточного отношения зубчатого механизма необходимо, чтобы нормаль к зацепляющимся профилям зубьев в точке контакта всегда проходила на линии центров через одну и ту же точку Р, называемую полюсом зацепления. Профили зубьев, удовлетворяющие этому условию, называются сопряженными.
В зубчатых механизмах величину передаточного отношения определяют через отношение чисел зубьев. Если умножить числитель и знаменатель отношения (3.4) на 2p, получат отношение длин начальных окружностей. Величина их может быть заменена произведением чисел зубьев на расстояние между одноименными профилями соседних зубьев (шаг по начальной окружности р), одинаковое для пары зацепляющихся колес:
(3.10)
Для зубчатых механизмов, составленных из конических колес, передаточное отношение определяется также по формуле (3.10).
В зубчатом зацеплении большее из двух колес называют колесом, а меньшее - шестерней. Отношение числа зубьев колеса (Zk) к числу зубьев шестерни (Zш) называют передаточным: U = Zk/Zш.
Рядовые механизмы. При необходимости получения большого передаточного отношения применяются механизмы, состоящие из нескольких пар колес, так называемые серии зубчатых колес. Серии зубчатых колес, у которых все валы колес вращаются в неподвижных подшипниках, называются рядовыми.
Определим передаточное отношение рядового механизма, состоящего из трех пар цилиндрических зубчатых колес (рис. 3.3, а). Колеса 2-3 и 4-5 жестко связаны между собой, т.е. вращаются с одинаковыми угловыми скоростями (w2 = w3; w4 = w5). Общее передаточное отношение механизма:
Запишем передаточное отношение для каждой зубчатой пары:
Перемножим правые и левые части этих уравнений:
(3.11)
Следовательно, передаточное отношение рядового зубчатого механизма равно произведению передаточных отношений отдельных зубчатых пар. Знак передаточного отношения рядового механизма при четном количестве внешних зацеплений положительный, при нечетном - отрицательный.
Для рядовых механизмов с коническими колесами знак передаточного отношения определяется по правилу стрелок (рис. 3.3, в): при одинаковом направлении стрелок, определяющих направление вращения колес, знак положительный, при противоположном - отрицательный.
Для передачи вращения между валами, далеко расположенными друг от друга, или для изменения направления вращения валов применяются механизмы, у которых имеются колеса, являющиеся ведомыми (по отношению к предыдущему) и ведущими (по отношению к предыдущему). В технике такие колеса называют паразитными. Передаточное отношение механизма с паразитными колесами (рис. 3.3, б) согласно формуле (3.11):
(3.12)
то есть равно отношению числа зубьев последнего ведомого колеса к числу зубьев первого ведущего. Значит, применение паразитных колес не влияет на величину передаточного отношения, но при изменении числа их от четного к нечетному меняется знак передаточного отношения.
Сателлитные механизмы
Рис.3.4. Схема сателлитного механизма с цилиндрическими зубчатыми колёсами.
Механизмы, имеющие колёса с подвижными осями, называются сателлитными. В механизме, приведённом на рисунке 3.4, зубчатые колёса 1 и 3, оси которых совпадают с основной геометрической осью механизма, называются центральными, колесо 2, совершающее сложное движение вокруг собственной оси и вокруг основной, называется сателлитом. Рычаг H, в котором закреплена подвижная ось сателлита, называется водилом. Центральные колесо и водило являются основными звеньями.
Степень подвижности механизма, изображённого на рис.3.4.,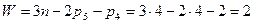 
Сателлитные механизмы, у которых подвижны все основные звенья и степень подвижности равна двум, служат для сложения движений и называются дифференциальными механизмами.
Для определения зависимостей между скоростями всех звеньев дифференциальной передачи 
воспользуемся способом обращения движения. Сообщим всему механизму вращение вокруг оси О1 со скоростью, равной скорости водила H, но направленной в противоположную сторону(
).
Тогда дифференциальный механизм превратится в механизм с неподвижными осями (
) и скоростями подвижных звеньев относительно водила 
; 
.
Передаточное отношение такого механизма 
(индекс H означает, что водило остановлено), как при рядовом соединении колёс выражается формулой:
(3.13.)
Численное значение передаточного отношения всегда можно определить по формулам (3.4.) и (3.11), зная радиусы окружностей, по которым перекатываются колёса (для фрикционного механизма), или числа зубьев, зацепляющихся колёс в зубчатых механизмах с обязательным учётом знака передаточного отношения.В общем случае для дифференциального механизма, состоящего из k колёс,
(3.14)
Эта формула носит название формулы Виллиса.
Если в сателлитном механизме (рис.3.4) на одно из центральных колёс наложена дополнительная кинематическая связь (например, 
), то получают планетарный механизм, степень подвижности которого 
, а формула Виллиса примет вид:
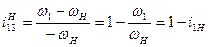, следовательно
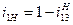(3.15)
с помощью планетарных механизмов можно совершать очень большие передаточные отношения при небольшом количестве колёс.
Замкнутые дифференциальные механизмы.
Рис.3.5. Схема замкнутого дифференциального механизма.
Механизмы, у которых два из трёх основных звеньев соединены между собой дополнительной передачей, называются замкнутыми. Так, в механизме, приведённом на рис.3.5, ведущее звено 1 и ведомое 3 замкнуты передачей с колёсами a,b,c,d. При определении передаточного отношения этого механизма в формуле Виллиса скорость одного из основных звеньев выражают через скорость текущего звена. В рассматриваемом случае 
, следовательно, на основании формул (3.15) и (3.13). 
,
откуда 
(3.16)
Конический дифференциал
Рис. 3.6. Конический дифференциал.
Конический дифференциал получил широкое применение в транспортных машинах, металлорежущих станках, а также во многих счётных машинах и приборах как суммирующий механизм.
На рис.3.6. представлена схема дифференциала автомобиля. От ведущего вала через коническую передачу a-b приводятся во вращение водило H, в котором смонтированы сателлиты 2 и 
. При вращении водила зубья сателлитов надавливают на центральные колёса 3 и 1, вследствие чего вращаются валы | и ||, связанные с колёсами заднего моста автомобиля.
Кинематические соотношения конического дифференциала (рис.3.6) определяется по формуле Виллиса. Числа зубьев центральных колёс 1 и 3 одинаковые, поэтому 
(стрелки направлены в противоположные стороны), и согласно формуле (3.13) угловая скорость водила 
. В автомобиле конический дифференциал позволяет производить перераспределение угловой скорости, полученной от карданного вала на ведущие колёса при движении по кривой. В другом случае эти механизмы позволяют производить сложение скоростей, получаемых от различных источников.
Волновые передачи
Рис. 3.7. Волновая передача: a- зона полного зацепления; б - частичного; с - зацепление отсутствует.
Волновая передача. (Рис. 3.7) состоит из жесткого 1 и гибкого 2 зубчатых колёс и генератора волн 3, составленных по схеме планетарное передачи. Вставленный в гибкое колесо генератор волн (водило) упруго деформирует его, превращая из круглого в эллиптическое. Числа зубьев жесткого Z2 и гибкого Z1 колёс не одинаковы, поэтому при неподвижном жестком колесе за один оборот генератора гибкое звено повернётся на число угловых шагов зубьев Z1-Z2. Вследствие того, что передача вращения осуществляется в механизме, имеющим подвижные оси, кинематические соотношения в таких механизмах определяются по формуле Виллиса при 
.
При неподвижном гибком колесе 2(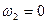
) передаточное отношение между генератором волн 3 (водилом) и жестким колесом 1 с учётом, что 
, 
,
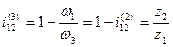откуда 
и 
(3.17)
При неподвижном жестком колесе 1 передаточное отношение между генератором и гибким колесом 2
(3.18)
