Принципы классификации. Для удобства изучения механизмов и разработки общих методов проектирования и расчета механизмы целесообразно классифицировать. Могут быть использованы разные признаки классификации: характер движения - плоские и пространственные; вид кинематических пар - механизмы с низшими и высшими парами; назначение - механизмы приборов для контроля давлений, температуры, уровня и т.д.; принцип передачи усилий - механизмы трения и зацепления; конструктивные признаки - шарнирно-рычажные, кулачковые, фрикционные, зубчатые, червячные и т.д. В зависимости от задач, поставленных перед исследователем, пользуются той или иной классификацией, лучше всего удовлетворяющей решению этих задач.
Структурная классификация. Одной из распространенных классификаций плоских шарнирных механизмов с парами пятого класса является структурная классификация, предложенная И.И. Артоболевским на основании идей Л.В. Ассура. Согласно этой классификации механизмы объединяются в классы от первого и выше по структурным признакам. Механизм первого класса состоит из ведущего звена и стойки, соединенных кинематической парой пятого класса; механизмы более высоких классов образуются последовательным присоединением к механизму первого класса кинематических цепей, не изменяющих степени подвижности этого исходного механизма, т.е. имеющих степень подвижности, равную нулю.
Группа. Кинематическая цепь, которая, будучи присоединенной свободными элементами пар (внешние пары) к стойке, обладает нулевой степенью подвижности, называется группой.
Полагая, что в состав группы входят только пары пятого класса (пары четвертого класса можно условно заменить цепями с парами пятого класса), для группы, как частного случая цепи, получаем условие W = 3n - 2p5 = 0, откуда:
р5 =  n (1.4)
n (1.4)
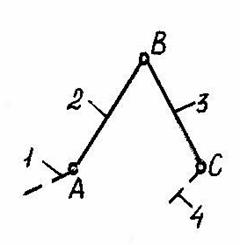
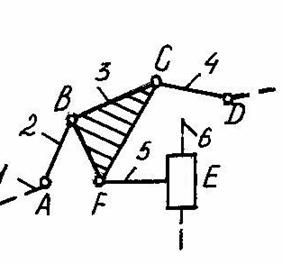
Таким образом, группа может состоять из двух подвижных звеньев и трех кинематических пар пятого класса (рис. 1.5, а), четырех подвижных звеньев и шести пар пятого класса (рис. 1.5, г, д) и т.д.
|
|
а) б) в)
|
г) д)
Рис. 1.5. Контуры различных классов
Контур и вид группы. Группы делятся на классы в зависимости от класса контура. Контуром называют замкнутую часть плоскости, занятую звеном или ограниченную со всех сторон звеньями. Класс контура определяется числом кинематических пар, входящих в этот контур. Контур, изображенный на рис. 1.5, б - второго класса (эквивалентное изображение дано на рис. 1.5, в). На рис. 1.5, д изображена группа, в состав которой входят три контура: АВС - контур третьего класса, BDFC - контур четвертого класса, DEF - контур третьего класса.
Класс группы определяется наивысшим классом контура, входящего в ее состав. Группа второго класса представлена на рис. 1.5, а, группы третьего и четвертого классов - на рис. 1.5, г и 5, д соответственно.
Наиболее распространенными являются группы второго класса, которые разделяют на пять видов. Вид группы второго класса определяется в зависимости от числа и относительного расположения поступательных и вращательных кинематических пар в ней (рис. 1.6, а - д).
|
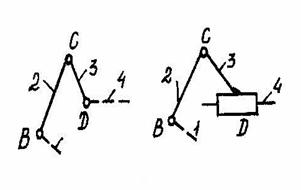
а) первого б) второго
вида вида


в) третьего г) четвёртого
вида вида
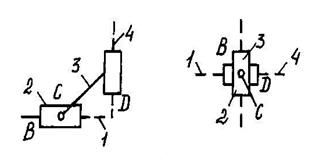
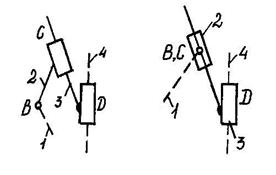
г) четвертого д) пятого
вида вида
Рис. 1.6. Группы второго вида
Класс механизма. По наивысшему классу группы, входящей в состав данного механизма, определяется его класс. Для определения класса механизма необходимо выделить в нем группы, начиная с наиболее удаленных от ведущего звена, в результате чего остается механизм первого класса. Выделив группу, одновременно проверяют степень подвижности W оставшейся части механизма.
Этот процесс исследования называется структурным анализом механизма. Порядок проведения структурного анализа: а) определяется количество подвижных звеньев и кинематических пар; б) устанавливается наличие пассивных связей и лишних степеней свободы, соответствующие звенья, вносящие их, исключаются; в) производится замена высших кинематических пар цепями с низшими парами; г) выделяются группы и устанавливается их класс и вид; д) определяется класс механизма.
Пример: Провести структурный анализ механизма привода конвейера (рис. 1.7, а).

а)



б) в) г)
Рис. 1.7. Структурный анализ привода конвейера
Механизм конвейера состоит из пяти подвижных звеньев (n = 5) и семи кинематических пар пятого класса (р5 = 7); пары четвертого класса отсутствуют (р4 = 0). Степень подвижности цепи по формуле W = 3n - р5 - р4 = 3*2 - 2*7 - 0 = 1, следовательно, эта цепь будет механизмом при заданном законе движения одного звена (звено 1). В механизме пассивных связей и лишних степеней свободы нет.
Переходим к выделению структурных групп, начиная со звеньев, наиболее удаленных от ведущего звена (рис. 1.7, б). Выделенные группы и порядок их выделения представлены на рис. 1.7, в, г. Каждая группа состоит из двух звеньев и трех кинематических пар пятого класса и поэтому является группой второго класса; первая группа (рис. 1.7, в) - второго вида (одна крайняя пара поступательная); вторая группа (рис. 1.7, г) - первого вида (все пары вращательные). Следовательно, механизм привода конвейера - второго класса, т.к. наивысший класс группы, входящей в состав этого механизма, второй.








