Скорости и ускорения ведомых звеньев механизма могут быть определены методами планов, кинематических диаграмм и аналитическими. Во всех случаях в качестве исходных данных должны быть известны: схема механизма при определенном положении ведущего звена, его скорость и ускорение.
Метод планов. Построение планов скоростей и ускорений проводится на основе последовательного составления векторных уравнений для всех групп, входящих в механизм, начиная с ведущего звена.
Для определения полной картины скоростей любого звена, входящего в группу, достаточно знать линейные скорости двух точек этого звена или линейную скорость одной точки и угловую скорость звена. Так как скорости конечных элементов звеньев групп известны, то необходимо выбрать общую для двух звеньев точку и записать два уравнения для определения скорости этой точки.
Для групп первого, второго и четвертого видов (рис. 2.3, а, б, г) это постоянная точка - центр средней вращательной пары группы, для других - мгновенная точка на одном звене, совпадающая в данный момент с центром конечной вращательной пары другого звена.
При составлении векторных уравнений следует четко установить точки, скорости которых используются как скорости в переносном движении. Если звенья группы образуют поступательные кинематические, то необходимо использовать точки, принадлежащие направляющим звеньям. В качестве примера рассмотрим построение планов скоростей и ускорений группы второго класса второго вида.
а)
б) в)
Рис. 2.3. Кинематическое исследование группы второго класса второго вида
План скоростей. В этой группе (рис. 2.3, а) полагаем, что скорости примыкающих звеньев 1 и 4 заданы. Следовательно, скорость точки В2, принадлежащей звену 2, равна скорости точки В1, принадлежащей звену 1, т.е. 
. Угловая скорость звена 3, образующего поступательную пару со звеном 4, равна заданной угловой скорости звена 4, т.е. w3 = w4. Следовательно, для отыскания скоростей второго звена достаточно определить, кроме известной скорости точки В, скорость еще одной точки, а для третьего звена, кроме известной угловой скорости w3, также скорость какой-либо одной точки. Для решения этой задачи следует рассмотреть движение общей для этих двух звеньев точки С - центра средней вращательной пары.
Рассмотрим движение звена 2 относительно звена 1. Эти звенья образуют вращательную пару, поэтому на основании теоремы о сложении скоростей в сложном движении скорость точки С на звене 2 складывается из скорости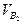 
переносного (поступательного) движения звена со скоростью 
и скорости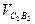 
относительного (вращательного) движения звена 2 вокруг точки В:
(2.6)
где 
Теперь определим скорость точки С, отнеся ее к 3 звену. Звено 3 образует со звеном 4 поступательную пару, поэтому скорость точки С3 можно представить как сумму двух скоростей: скорости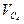 
точки С4, совпадающей с точкой С3 и принадлежащей среде переноса (в данном случае примыкающему звену 4), и скорости точки С3 относительно точки С4 в поступательном движении звена 3 относительно звена 4 - 
, т.е.:
(2.7)
Точку С4 расположим на плоскости, жестко связанной со звеном 4. Зная закон движения этого звена, можно найти мгновенный цент? вращения (МЦВ) и при известном расстоянии его от точки С4 и угловой скорости w4 определить величину и направление скорости этой точки.
Систему уравнений (2.6) и (2.7) решим графически в выбранном масштабе 
(
) на плане скоростей (рис. 2.3, б). Откладываем от полюса рv параллельно вектору скорости точки В отрезок pv в (мм) и через конец этого отрезка проводим прямую, являющуюся линией действия вектора VCB. Эта прямая перпендикулярна к линии ВС.
Далее из полюса pv плана скоростей параллельно вектору 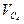(рис. 2.3, а) откладываем отрезок pvc4 = 
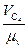(мм). Через конец этого отрезка (точку С4) проводим прямую, параллельную направляющей поступательной пары D, являющейся линией действия вектора относительной поступательной скорости 
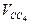. Так как 
, векторные суммы определяются точкой пересечения линий действия относительных скоростей. Точку пересечения этих линий обозначим С, абсолютная скорость точки С определится из условия
Vc = (pvc) 
v.
Из плана скоростей получим также величины и направления векторов относительных скоростей: вращательной VCB - отрезок bc и поступательной 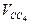- отрезок C4C. Угловая скорость второго звена:
, (2.8)
а направление ее определяется мысленным переносом вектора относительной скорости VСВ - отрезка bc плана скоростей в точку С на плане положения группы.
Пользуясь планом скоростей, можно найти скорость любой точки на звене. Скорость точки S на втором звене определяется из условия представления сложного движения звена 2 как поступательного со скоростью VB и вращательного вокруг точки В, а также как поступательного со скоростью Vc и вращательного вокруг точки С:
} (2.9)
Решая эту систему графически, определяют точку S - конец вектора VS.
Из построения следует, что треугольник csb на плане скоростей подобен треугольнику CSB на плане положений группы и повернут относительно него на 90°. Правильность построения определяется одинаковым порядком букв при обходе контура звена и контура относительных скоростей на плане скоростей в одном и том же направлении.
План ускорений. Исходными данными для построения плана ускорений являются план положения группы, план скоростей (рис. 2.3, а, б) и ускорения звеньев, примыкающих к данной группе. При построении плана ускорений полностью применимы рассуждения, использованные при решении задачи об отыскании скоростей звеньев. Ускорение точки В2 известно, т.к. она совпадает с точкой В1, т.е. 
, угловое ускорение звена 3 известно, т.к. оно образует со звеном 4 поступательную пару, т.е. e3=e4. 
Для нахождения ускорения любой точки звеньев 2 и 3 дополнительно надо знать ускорение хотя бы одной точки на каждом из этих звеньев. В качестве такой точки следует использовать центр шарнира С, являющийся общей точкой для звеньев 2 и 3. Рассматривая вращательное движение звена 2 вокруг точки В и поступательное - звена 3 относительно звена 4, записываем следующие векторные уравнения:
} (2.10)
Систему уравнений (2.10) решим графически. На чертеже (рис. 2.3, в) обозначим полюс плана ускорений ра и выберем масштаб построения плана ускорений 
. Откладываем от полюса ра параллельно вектору ускорения аВ отрезок 
(мм). Нормальное ускорение аСВn точки С в относительном движении направлено от точки С вдоль звена 2 к точке В; величину его, исходя из построенного плана скоростей (рис. 2.3, б), определим по формуле:
(2.11)
Из точки b плана ускорений проводим линию действия ускорения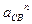 
в направлении от точки С к точке В и откладываем отрезок 
.
Из точки n перпендикулярно к отрезку bn проводим линию действия тангенциального ускорения 
. Далее из полюса ра проводим линию параллельно известному направлению ускорения 
(рис. 2.3, а) и откладываем отрезок:
Ускорение Кориолиса (поворотное ускорение):
(2.12)
откладываем на плане ускорения в виде отрезка 
(мм). Направление указанного отрезка определяется путем поворота вектора относительной скорости С4С на 90° в сторону
вращения среды поворота - звена 4. Из точки К проводим линию действия ускорения 
, параллельную направляющей поступательной пары, т.е. перпендикулярно к вектору ускорений 
. Пересечение линий действия и 
определит наложение точки C.
Из плана ускорения получим также величины и направления векторов относительных ускорений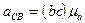 
(м/с2) и 
(м/с2). Угловое ускорение звена 2 определится по формуле:
e 
(2.13)
Направление e2 устанавливается путем мысленного переноса вектора nc в точку С и определения направления вращения звена 2 вокруг точки В под влиянием этого вектора.
Пользуясь планом ускорений, можно найти ускорение любой точки на звене 2 и 3. Например, требуется определить ускорение точки S на звене 2. На основании известного положения о подобии фигур звена и плана относительных ускорений строим на отрезке bc плана ускорений треугольник csb, подобный треугольнику CSB на звене 2, соблюдая при этом одинаковую последовательность расположения букв при обходе контуров этих треугольников в одном направлении. Соединяя полученную в результате построения точку S с полюсом ра, получаем отрезок pas, определяющий в масштабе ускорение точки S:as = (pas)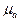 
Аналитический метод. Этот метод позволяет определять скорости и ускорения с более высокой точностью. Обычно применяют метод последовательного дифференцирования функции перемещения точки, скорость и ускорение которой необходимо определить. Функцию перемещения S=S(t) или S=S(j) можно получить из геометрических соображений, как, например, это сделано для кривошипно-ползунного механизма - формула (2.5), а ее скорость и ускорение - путем дифференцирования уравнений (2.3).
Дифференцируя уравнения (2.3) по обобщенной координате j1 (углу поворота ведущего звена), получают не истинную угловую скорость, а безразмерную величину 
, получившую название аналога угловой скорости. Связь между аналогом скорости и действительной угловой скоростью i-го звена определится из соотношения:
,
т.е. угловая скорость i-го звена wi равна произведению угловой скорости ведущего звена wi на аналог скорости. Продифференцировав уравнения (2.3) и подставив значение аналога скорости, получаем уравнения для определения угловой скорости, получаем уравнения для определения угловой скорости шатуна w2 (рис. 2.2) и относительной скорости звена 3 - u30=uс:
(2.17)
Определим значение w2 из второго уравнения (2.17):
и подставим его в первое уравнение, с учетом формулы (2.4), получим значение uс:
(2.18)
При вторичном дифференцировании уравнений (2.3) с использованием понятия аналога углового ускорения, представляющего вторую производную по углу поворота ведущего звена 
, можно определить действительное ускорение i-го звена, умножив аналог углового ускорения на квадрат угловой скорости ведущего звена w12. При этом принимая, что w1= const, получают уравнения для определения углового ускорения шатуна e2 и относительного ускорения звена 
(2.19)
из уравнения (2.19) получим значение:
.
Получив значения угловых скоростей и ускорений, можно определить скорость и ускорение любой точки звеньев механизма. В тех случаях, когда l £ 1/3, пользуются приближенными формулами при определении перемещения, скорости и ускорения ползуна. При этом перемещение ползуна Sc измеряем от мертвого положения Со (рис. 2.2):
Sc = l1 + l2 - Xc, или с учетом (2.5) получим:
(2.20)
Раскладывая в ряд радикал, входящий в формулу (2.20) по биному Ньютона и ограничиваясь его первыми двумя членами, получим:
(2.21)
После дифференцирования скорость uс и ускорение ас определяют по формулам:
uс @ w1l1 (sinj1 + l/2 sin 2j1) (2.22)
aс @ w12l1 (cosj1 + lcos 2j1) (2.23)
