Некруглые колёса.
Рис.3.8 Схема механизма с некруглыми колёсами.
В машиностроении механизмы с некруглыми колёсами применяются при передаче движения с переменным передаточным отношением, при небольших угловых скоростях и параллельном расположении осей, а в приборостроении – чаще всего для воспроизведения нелинейных функций. Наибольше распространение получили некруглые колёса, центроиды которых имеют форму эллипса (рис 3.8). При их проектировании необходимо выполнить условие, чтобы сумма двух любых сопряжённых радиус-векторов была равна межосевому расстоянию:
Теория проектирования некруглых колёс рассматривается в специальной литературе.
Кулачковые механизмы.
Рис.3.9. Схема кулачкового механизма с поступательно движущимся толкателем.
Кинематический анализ кулачкового механизма сводится к определению скорости толкателя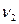 
при заданной угловой скорости кулачка 
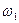для этой цели часто пользуются графическим способом определения скоростей и ускорений толкателя, используя метод графического дифференцирования графика перемещений толкателя. Применяют также метод планов скоростей и ускорений. Перемещение толкателя для различных положений кулачка (рис.3.9) определяют способом засечек в сочетании с методом обращения движения.
Рассмотрим внецентренный кулачковый механизм (рис.3.9), ведущее звено которого (кулачок) очерчено рабочим профилем 
. Нанесём теоретический профиль – равноотстоящую от рабочего профиля кривую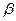 
, проходящую через центр ролика B. Придадим всему механизму вращение со скоростью (
); кулачок остановится, а толкатель 2 будет совершать поступательные движения со скоростью 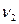и вращательное со скоростью () так, что центр ролика B будет двигаться по кривой 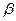. Если из центра О1 провести окружность радиусом l, то длина касательных к этой окружности от основания до пересечения с кривой 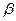будет характеризоваться положениями толкателя относительно кулачка. График перемещения толкателя получим, если по оси абсцисс отложить в масштабе время одного оборота кулачка, а по оси ординат – разность длин касательных, проведённых к окружности радиуса l, в рассматриваемый момент времени и момент, соответствующий наилучшему положению толкателя (например, 4B4 – 3В3 и т.д.).
Рис.3.10. к аналитическому анализу внецентренного кулачкового механизма.
Для кулачковых механизмов, применяемых для точного воспроизведения заданного движения ведомого звена (приборостроении, счетно-решающие устройства, быстроходные механизмы и др.), используют аналитический метод кинематического исследования. Установим кулачок так, чтобы толкатель занимал крайнее положение 
(рис3.10).Проведём оси координат x и y через центр вращения кулачка О и соединим начало координат О с точкой профиля кулачка А, расположенной на максимальном расстоянии от центра О и точкой радиус-векторами 
и 
, равными радиусу основной шайбы 
(наименьшему вектору профиля кулачка). При повороте кулачка на угол 
точка А займёт положение 
будет представлять собой перемещение толкателя. Из рис3.10 следует, что
(3.19)
где 
, а 
и 
.
Задаваясь углом 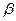, находим текущий радиус-вектор и угол поворота кулачка 
. Таким образом устанавливается связь между углом поворота кулачка и перемещением толкателя S. Скорость и ускорение толкателя определяют по формулам
;
;
Полученные зависимости для внецентренного кулачкового механизма приемлемы и для центральных кулачковых механизмов, у которых смещение l=0. При этом условии 
и, следовательно, закон изменения перемещения S толкателя с остриём.
