При выполнении работы студенты должны руководствоваться общими для учебных аудиторий правилами техники безопасности.
Методика и порядок выполнения работы
Согласно заданию (таблица 1.1), определить в установившемся режиме предельные значения:
- относительной пропускной способности  ;
;
- абсолютной пропускной способности 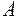 ;
;
- вероятности отказа  .
.
Таблица 1.1 – Исходные данные
| № варианта | Время обслуживания t, с | Интенсивность поступления заявок  , ед/с , ед/с
| Максимальное количество требований (заявок) 
| Количество каналов, n |
| 2,1 | ||||
| 2,15 | ||||
| 2,2 | ||||
| 2,25 | ||||
| 2,2 | ||||
| 2,15 | ||||
| 2,1 | ||||
| 2,05 | ||||
| 1,95 | ||||
| 1,9 |
Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно t часов и автомобили следовали один за другим без перерыва.
Содержание отчета и его форма
Отчет должен содержать:
6.1 Расчет относительной пропускной способности  ;
;
6.2 Расчет абсолютной пропускной способности 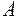 ;
;
6.3 Расчет вероятности отказа  ;
;
6.4 Выводы.
Контрольные вопросы и защита работы
7.1 Что такое относительная пропускная способность системы?
7.2 Какие вероятностные состояния у данной системы?
7.3 Как определяется пропускная способность системы при стационарном (установившемся) режиме?
7.4 Что такое абсолютная пропускная способность?
7.5 Чему равна вероятность отказа в обслуживании заявки?
Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы, представленные выше.
Практическое занятие 13.
Определение характеристик одноканальной системы массового обслуживания с ожиданием
Цель и содержание
Цель работы – приобрести навыки моделирования одноканальной системы массового обслуживания с ожиданием.
В результате выполнения работы студенты должны:
1. Определить вероятность отказа в обслуживании заявки;
2. Определить относительную пропускную способность;
3. Определить абсолютную пропускную способность;
4. Определить среднее число находящихся в системе заявок;
5. Определить среднее время пребывания заявки в системе;
6. Определить среднюю продолжительность пребывания клиента в очереди;
7. Определить среднее число заявок в очереди;
8. Сделать выводы.
Теоретическое обоснование
Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание – простейший поток с интенсивностью  . Интенсивность потока обслуживания равна
. Интенсивность потока обслуживания равна  (т. е. в среднем непрерывно занятый канал будет выдавать
(т. е. в среднем непрерывно занятый канал будет выдавать  обслуженных заявок). Длительность обслуживания – случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
обслуженных заявок). Длительность обслуживания – случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + + обслуживаемые клиенты) не может вместить более  – требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость.
– требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость.
Состояния СМО имеют следующую интерпретацию:
 – канал свободен;
– канал свободен;
 – канал занят, очереди нет;
– канал занят, очереди нет;
 – канал занят, одна заявка стоит в очереди;
– канал занят, одна заявка стоит в очереди;
....................................
 – канал занят,
– канал занят,  заявок стоит в очереди;
заявок стоит в очереди;
....................................
 – канал занят,
– канал занят,  заявок стоит в очереди.
заявок стоит в очереди.
Стационарный процесс в данной системе будет описываться следующей системой алгебраических уравнений:

| (2.1) |
где  ;
;
 – номер состояния.
– номер состояния.
Решение приведенной выше системы уравнений для нашей модели СМО имеет вид:

| (2.2) |
 , ,
| (2.3) |
тогда
Следует отметить, что выполнение условия стационарности  для данной СМО не обязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать
для данной СМО не обязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать  ), а не соотношением между интенсивностями входного потока, т. е. не отношением
), а не соотношением между интенсивностями входного потока, т. е. не отношением  .
.
Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной ( ):
):
- вероятность отказа в обслуживании заявки равна:

| (2.4) |
- относительная пропускная способность системы:

| (2.5) |
- абсолютная пропускная способность:
 . .
| (2.6) |
- среднее число находящихся в системе заявок:

| (2.7) |
- среднее время пребывания заявки в системе:
 ; ;
| (2.8) |
- средняя продолжительность пребывания клиента (заявки) в очереди:
 ; ;
| (2.9) |
- среднее число заявок (клиентов) в очереди (длина очереди):
 . .
| (2.10) |






