Получить вариант задания (таблица 5.1)
Таблица 5.1 – Исходные данные
| Вариант | Условия моделирования |
Периодичность поступления заявок на обслуживание подчинена показательному закону распределения. Средний интервал между поступлениями заявок в систему равен  часа. Определить последовательность значений продолжительности интервалов между поступлениями заявок. Число реализаций равно 10. часа. Определить последовательность значений продолжительности интервалов между поступлениями заявок. Число реализаций равно 10.
| |
Время обслуживания работника предприятия кассой бухгалтерии является случайной величиной, распределенной в соответствии с законом Вейбула. Среднее время обслуживания  мин, среднеквадратическое отклонение равно мин, среднеквадратическое отклонение равно  мин. Требуется смоделировать случайную величину, отвечающую этим условиям. Число реализаций принять равным 10. мин. Требуется смоделировать случайную величину, отвечающую этим условиям. Число реализаций принять равным 10.
| |
При обработке экспериментальных данных было установлено, что время, расходуемое на станции технического обслуживания автомобилей для замены двигателя, распределено по нормальному закону, параметры которого равны  часа на один двигатель и часа на один двигатель и  часа. Требуется смоделировать для отмеченных условий случайную величину – время часа. Требуется смоделировать для отмеченных условий случайную величину – время  , расходуемое для замены двигателя. Число реализаций принять равным 5. , расходуемое для замены двигателя. Число реализаций принять равным 5.
| |
Время проверки приемки квартального отчета инспектором налоговой службы ( ) величина случайная, распределенная в соответствии с законом Вейбула. Среднее время проверки и приемки равно ) величина случайная, распределенная в соответствии с законом Вейбула. Среднее время проверки и приемки равно 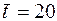 мин. Коэффициент вариации величины мин. Коэффициент вариации величины  равен равен  . Требуется смоделировать для заданных условий случайные числа . Требуется смоделировать для заданных условий случайные числа  (число реализаций принять равным 10). (число реализаций принять равным 10).
| |
Среднее число исправных станков в токарном цехе на заводе равно  . Среднеквадратическое отклонение равно . Среднеквадратическое отклонение равно  . Требуется смоделировать число исправных станков в цехе (число реализаций равно пяти) при условии, что случайная величина . Требуется смоделировать число исправных станков в цехе (число реализаций равно пяти) при условии, что случайная величина  имеет гамма-распределение. имеет гамма-распределение.
| |
Вероятность замены неисправной детали на новую при ремонте автомобиля в каждом испытании равна  . Смоделировать пять испытаний и определить последовательность замены детали на новую или восстановленную. . Смоделировать пять испытаний и определить последовательность замены детали на новую или восстановленную.
| |
| При испытании могут иметь место зависимые и совместные три события: работает только первый кассир по выдаче заработной платы, работает только второй кассир, работают оба кассира. При этом известно, что вероятность работы первого кассира равна 0,6; вероятность работы второго кассира равна 0,7; вероятность работы двух кассиров равна 0,4. Смоделировать возможность реализации двух событий: работает только первый кассир; работает только второй кассир в трех испытаниях. | |
| Сохраняются условия задачи 7. Определить номер интервала, в который попадет максимальное количество отказов. | |
Система имеет два элемента. Средняя периодичность первого элемента равна  час., второго элемента – час., второго элемента –  час. Периодичности отказа первого и второго элемента – случайные величины, подчиненные экспоненциальному закону распределения. Определить параметр и функцию распределения потока отказов системы по интервалам времени час. Периодичности отказа первого и второго элемента – случайные величины, подчиненные экспоненциальному закону распределения. Определить параметр и функцию распределения потока отказов системы по интервалам времени  час. Число реализации принять равным час. Число реализации принять равным  . .
| |
| Сохраняются условия задачи 9. Определить номера интервалов, в которые попадут максимальные количества отказов первого, второго элемента и в целом всей системы. | |
Пусть при испытании могут иметь место зависимые и совместные события 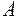 и и  . Известно, что вероятности появления событий равны . Известно, что вероятности появления событий равны  ; ;  , а также вероятность совместного появления событий , а также вероятность совместного появления событий 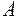 и и  : :  . Смоделировать появление событий . Смоделировать появление событий 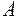 и и  в пяти испытаниях. в пяти испытаниях.
| |
Периодичность проверки предприятий налоговой инспекции величина случайная (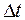 ), подчиняющаяся закону гамма-распределения. Средний интервал поверки равен ), подчиняющаяся закону гамма-распределения. Средний интервал поверки равен 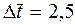 месяца. Коэффициент вариации величины месяца. Коэффициент вариации величины 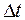 равен равен  . Требуется смоделировать для заданных условий возможные моменты проверок предприятия налоговой инспекцией (число реализаций принять равным 10). . Требуется смоделировать для заданных условий возможные моменты проверок предприятия налоговой инспекцией (число реализаций принять равным 10).
| |
| Сохраняются условия задачи 12. Определить количество проверок налоговой инспекцией за первый год работы предприятия. | |
Среднее число работающих машин на заводе равно  . Коэффициент вариации числа работающих равен . Коэффициент вариации числа работающих равен  . Требуется смоделировать число работающих машин на заводе (число реализаций равно 10). Случайная величина . Требуется смоделировать число работающих машин на заводе (число реализаций равно 10). Случайная величина  имеет распределение Вейбула. имеет распределение Вейбула.
| |
После каждой проверки предприятия налоговой инспекцией вероятность появления необходимости аудиторской проверки данного предприятия равна  . Смоделировать шесть испытаний. Определить последовательность проведения различных проверок предприятия. . Смоделировать шесть испытаний. Определить последовательность проведения различных проверок предприятия.
|
Определить параметры модели;
Смоделировать случайную величину, распределенную по заданному закону;
Построить гистограмму распределения случайной величины;
Произвести оценку качества;
Сделать выводы.
Содержание отчета и его форма
Отчет должен содержать:
6.1 Расчет параметров модели;
6.2 Расчет случайной величины, распределенной по заданному закону;
6.3 Гистограмму распределения случайной величины;
6.4 Оценку качества;
6.5 Выводы.
Контрольные вопросы и защита работы
7.1 В чем заключается решение задачи методом статистического моделирования?
7.2 Какой способ получения последовательности случайных чисел Вам известен?
7.3 Как определить плотность распределения экспоненциального закона?
7.4 Как определить плотность распределения Вейбула?
7.5 Как определить плотность гамма-распределения?
7.6 Как определить плотность распределения нормального закона?
Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы, представленные выше.
Практическое занятие 17.
Графическое решение задачи линейного программирования
Цель и содержание
Цель работы – приобрести навыки решения задач линейного программирования графическим методом.
В результате выполнения работы студенты должны:
1. Построить прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки равенств;
2. Найти полуплоскости, определяемые каждым из ограничений задачи;
3. Определить многоугольник решений;
4. Построить вектор  ;
;
5. Построить прямую 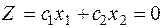 , проходящую через начало координат и перпендикулярную вектору
, проходящую через начало координат и перпендикулярную вектору  ;
;
6. Определить координаты точки максимума функции и вычислить значение целевой функции в этой точке;
7. Сделать выводы.
Теоретическое обоснование
Графический способ решения задач линейного программирования целесообразно использовать:
- при решении задач с двумя переменными, когда ограничения выражены неравенствами,
- для решения задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.
Запишем задачу линейного программирования с двумя переменными:
- целевая функция:
 ; ;
| (6.1) |
- ограничения:

| (6.2) |
 . .
| (6.3) |
Каждое из неравенств (6.1)–(6.2) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми  . В том случае, если система неравенств (6.2), (6.3) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых решений является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки равенств. Областью допустимых решений (7.35)–(7.36) может быть:
. В том случае, если система неравенств (6.2), (6.3) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых решений является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки равенств. Областью допустимых решений (7.35)–(7.36) может быть:
- выпуклый многоугольник,
- выпуклая многоугольная неограниченная область,
- пустая область,
- луч,
- отрезок,
- единственная точка.
Целевая функция (6.1) определяет на плоскости семейство параллельных прямых, каждой из которых соответствует определенное значение Z.
Вектор  с координатами
с координатами  и
и  , перпендикулярный к этим прямым, указывает направление наискорейшего возрастания
, перпендикулярный к этим прямым, указывает направление наискорейшего возрастания  , а противоположный вектор – направление убывания
, а противоположный вектор – направление убывания  .
.
Если в одной и той же системе координат изобразить область допустимых решений системы (6.2)–(6.3) и семейство параллельных прямых (6.2), то задача определения максимума функции  сведется к нахождению в допустимой области точки, через которую проходит прямая из семейства
сведется к нахождению в допустимой области точки, через которую проходит прямая из семейства  =const, которая соответствует наибольшему значению параметра
=const, которая соответствует наибольшему значению параметра  .
.
Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня 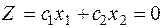 , проходящую через начало координат и перпендикулярную вектору
, проходящую через начало координат и перпендикулярную вектору  , и будем передвигать ее в направлении вектора
, и будем передвигать ее в направлении вектора  до тех пор, пока она не коснется последней крайней, угловой точки многоугольника решений. Координаты указанной точки и определяют оптимальный план данной задачи.
до тех пор, пока она не коснется последней крайней, угловой точки многоугольника решений. Координаты указанной точки и определяют оптимальный план данной задачи.
Заканчивая рассмотрение геометрической интерпретации задачи (6.1)–(6.3), отметим, что при нахождении ее решения могут встретиться случаи, изображенные на рис. 6.1–6.4. Рис. 6.1 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А. Из рис. 6.2 видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ.

На рисунке 6.3 изображен случай, когда максимум недостижим, а на рис.6.4 – случай, когда система ограничений задачи несовместна. Отметим, что нахождение минимального значения  при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня
при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня  передвигается не в направлении вектора
передвигается не в направлении вектора  , а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
, а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
Для практического решения задачи линейного программирования на основе ее геометрической интерпретации необходимо:
1. Построить прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки равенств.
2. Найти полуплоскости, определяемые каждым из ограничений задачи.
3. Определить многоугольник решений.
4. Построить вектор  .
.
5. Построить прямую 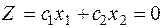 , проходящую через начало координат и перпендикулярную вектору
, проходящую через начало координат и перпендикулярную вектору  .
.
6. Передвигать прямую  в направлении вектора
в направлении вектора  , в результате чего либо находят точку (точки), в которых целевая функция принимает максимальное значение, либо устанавливают неограниченность функции сверху на множестве планов.
, в результате чего либо находят точку (точки), в которых целевая функция принимает максимальное значение, либо устанавливают неограниченность функции сверху на множестве планов.
7. Определить координаты точки максимума функции и вычислить значение целевой функции в этой точке.
Аппаратура и материалы
Микрокалькулятор, программное обеспечение MS Excel.






