При аппроксимации эмпирических данных возможны случаи, когда одни и те же данные могут быть одинаково успешно описаны несколькими распределениями. Поэтому необходима проверка согласия между распределением случайной величины, полученной по результатам наблюдений с предполагаемым теоретическим распределением этой величины. Всегда предпочтительнее выбирать то распределение, которое дает наибольшую вероятность согласия.
Решение этой задачи основано на использовании фундаментального положения математической статистики, согласно которому эмпирическая функция распределения сходится по вероятности к теоретической при неограниченном увеличении размера выборки, если выборка принадлежит рассматриваемому теоретическому распределению.
Проводим проверку принадлежности массива опытных данных к выбранному закону распределения по критериям согласия Колмогорова, Пирсона и Романовского.
Определение согласия данных по критерию Колмогорова
Максимальное отклонение функции эмпирического распределения от функции теоретического обозначается Dn:
. (24)
Для нахождения максимального отклонения расчеты необходимо представить в виде таблицы:
Таблица 4 - Последовательность расчета максимального отклонения
| Fэ(ti) | F(ti) | Fэ(ti) - F(ti) |
| ………. | |||
Вычисляется величина:
. (25)
Задаемся доверительной вероятностью:
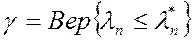, (26)
что отклонение Fэ(ti) от F(ti) будет меньше табличной величины 
(таблица А.3 приложения), установленной для доверительной вероятности g. Если уравнение (26) переписать в виде:
(27)
и вычисленная вероятность 1- g получается незначительной (меньше 0,1), то отклонение эмпирической функции распределения от теоретической неслучайно. Иначе говоря, Fэ(ti) плохо согласуется с F(ti). Если же разность 1- g велика (больше 0,3−0,4), то расхождение между Fэ(ti) и F(ti) считается несущественным и гипотеза о функции распределения считается согласованной с экспериментальными данными.
Определение согласия данных по критерию Пирсона c2
Широкое применение критерия c2 обосновывается легкостью его использования для проверки согласия любого распределения.
Первоначально определяется вероятность попадания значений случайной величины в каждый интервал:
. (28)
Находим теоретическую частоту попадания случайной величины в каждый интервал:
. (29)
Находим значения критерия согласия Пирона для каждого интервала:
. (30)
Значение критерия согласия Пирсона для всей выборки:
c2 = S(
). (31)
Чем меньше полученное значение c2 , тем лучше согласие между эмпирическим и теоретическим распределением.
Определяем число степеней свободы:
L= k – r – 1, (32)
где r – число параметров теоретической функции распределения, для нормального закона r = 2;
k - число интервалов.
После вычисления c2 задаемся доверительной вероятностью g (g =0,2…0,3) того, что величина c2, полученная в результате случайных отклонений частот эмпирического распределения от соответствующих частот теоретического распределения будет меньше табличного значения (c2*), установленного для выбранной доверительной вероятности g.
Если вычисленное значение c2 будет меньше (c2*), то для принятой доверительной вероятности g гипотеза о согласии эмпирического и теоретического распределения не отвергается, в противном случае ее необходимо проверять дальше. Если вычисленное значение c2 > (c2*) необходимо сравнить фактические частоты попадания в интервалы с ожидаемыми, чтобы увидеть, какие интервалы оказывают наибольшее влияние на величину c2. Это сравнение наглядно показывает характер отклонения от принятой теоретической модели.
Проверка по критерию согласия Романовского
Для проверки используется критерий:
. (33)
В случаях, когда вычисленная величина по своему абсолютному значению меньше 3, отклонение между эмпирическим и теоретическим распределениями считается несущественным, а выбранная модель закона распределения отражает эмпирические данные. Там, где полученное значение отклонения больше 3, расхождение между распределениями считается существенным, а модель теоретического распределения не отражает эмпирические данные.
Задание.
Согласно исходным данным (Практическое занятие 2) определить числовые характеристики распределения и построить эмпирическую и теоретическую функцию распределения.
Вопросы.
3.1 Как определяется количество интервалов?
3.2 Наиболее часто используемые характеристики случайной величины.
3.3 Что такое функция распределения?
3.4 Что такое функция плотности распределения?
3.5 Что такое медиана и мода случайной величины?
Практическое занятие 5, 6
Исследование распределения временных интервалов в транспортном потоке
Цель и содержание
Цель работы – приобрести навыки исследования распределения временных интервалов в транспортном потоке.
В результате выполнения работы студенты должны:
1. Определить временные интервалы между автомобилями.
2. Построить распределение временных интервалов.
3. Выдвинуть гипотезу о применении того или иного закона распределения.
4. Оценить тесноту связи теоретического закона с фактическим распределением.
5. Сделать выводы.
Теоретическое обоснование
Для статистического моделирования транспортного потока одной из важнейших характеристик является распределение интервалов между движущимися транспортными средствами во времени, а точнее – закон распределения временных интервалов в транспортном потоке. Закон распределения интервалов между автомобилями важен не только сам по себе. Он содержит также информацию об интенсивности движения. Она вычисляется как величина, обратная среднему интервалу:
 .
| (1.1) |
На основе закона распределения интервалов можно найти закон распределения интенсивности движения.
Наиболее надежным способом определения закона распределения являются экспериментальные исследования. Проведенные исследования (величиной выборки 
) над транспортным потоком выявили, что распределение случайной величины может быть подчинено предположительно логарифмически нормальному или гамма-распределению (рисунок 1.1).
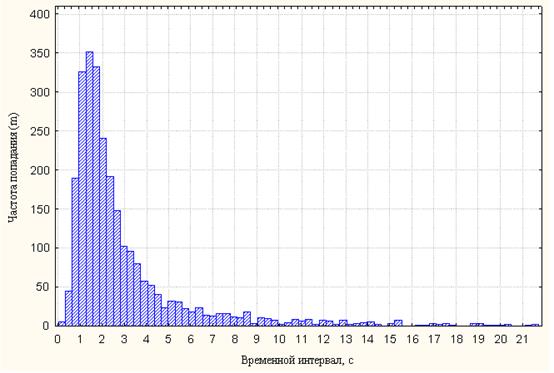
Рисунок 1.1 – Гистограмма распределения временных интервалов в потоке интенсивностью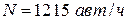 
Функция плотности вероятности логарифмически нормального распределения определяется по формуле:
| (1.2) |
где 
– временной интервал, с
– среднее квадратическое отклонение (для данного распределения 
);
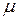– медиана (для данного распределения 
);
Графически кривая логнормального распределения представлена на рисунке 1.2.
Функция плотности вероятности гамма-распределения определяется по формуле:
 ,
| (1.3) |
где 
– параметры распределения (для данного распределения 
);
– гамма-функция Эйлера.
Графически кривая гамма-распределения представлена на рисунке 1.2.
Рисунок 1.2 – Теоретические распределения: а – логнормальное, б – гамма-распределение
В качестве критерия проверки надежности удобнее всего использовать критерий В. И. Романовского, основанный на применении критерия согласия 
:
 ,
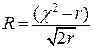| (1.4) |
где 
– число степеней свободы.
Для логнормального распределения 
, для гамма-распределения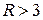 
, что говорит о существенном расхождении последнего распределения.
Действительно, логнормальное распределение при заданных условиях отражает структуру транспортного потока (рисунок 1.3). Автомобили в потоке двигаются друг за другом на минимально безопасном расстоянии (зона 2). Расстояния, меньшие наиболее частого интервала (моды распределения) соответствуют доле водителей, которые совершают обгон или двигаются с большим риском (зона 1). Значения, расположенные по правую сторону от моды (зона 3) распределения принадлежат транспортным средствам различных типов (автобусы, грузовые автомобили и т. д.) и различным маловероятным интервалам.
Рисунок 1.3 – Характерные зоны кривой распределения
Следует отметить, что применимость данного закона распределения не является абсолютной, поскольку на его характер влияет множество факторов: интенсивность движения, состав транспортного потока, дорожные условия.
Аппаратура и материалы
Микрокалькулятор, программное обеспечение MS Excel.
