| Возраст, лет (х) | Численность лиц данного возраста (f) | Середина интервала | x*f |  
| f
|
| До 25 | 449,44 | 6741,6 | |||
| 25-35 | 125,44 | 4641,28 | |||
| 35-45 | 1,44 | 102,24 | |||
| 45-55 | 77,44 | 3484,8 | |||
| 55 и более | 353,44 | 7775,68 | |||
| Итого | - | - | 22745,6 |
=10,94.
Средняя ошибка выборки составит:
года.
Определим с вероятностью 0,954 (t=2) предельную ошибку выборки:
года.
Установим границы генеральной средней:
41,2-1,6≤ 
≤41,2+1,6
или
39,6≤ ≤42,8.
Таким образом, на основании проведенного выборочного обследования с вероятностью 0,954 можно заключить, что средний возраст незанятого населения, ищущего работу, лежит в пределах от 40 до 43 лет.
Б). По выборочным данным определим долю лиц в возрасте до 25 лет и расчитаем дисперсию доли:
w=15/ 190=0,079;
Рассчитаем среднюю ошибку выборки:
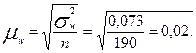
Предельная ошибка выборки с заданной вероятностью составит:
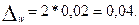
Определим границы генеральной доли:
0,079-0,04≤р≤0,079+0,04
или
0,039≤р≤0,119.
Следовательно, с вероятностью 0,954 можно утверждать, что доля лиц в возрасте до 25 лет в общей численности незанятого населения находится в пределах от 3,9 до 11,9%.
· При расчете средней ошибки собственно- случайной бесповторной выборки необходимо учитывать поправку на бесповторность отбора:
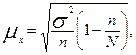
где N- объем (число единиц) генеральной совокупности.
· Необходимый объем собственно- случайной повторной выборки определяется по формуле:
n=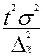 
.
Если отбор бесповторный, то формула приобретает следующий вид:
n= 
.
Полученный на основе использования этих формул результат всегда округляется в большую сторону до целого значения.
Например. Определите, сколько учащихся первых классов школ района необходимо отобрать в порядке собственно-случайной бесповторной выборки, чтобы с вероятность 0,997 определить границы среднего роста первоклассников с предельной ошибкой 2 см. Известно, что в первых классах школ района обучается 1100 учеников, а дисперсия роста по результатам аналогичного обследования в другом районе составила 24.
Решение.
Необходимый объем выборки при уровне вероятности 0,997 (t=3) составит:
n=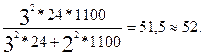 
Таким образом, для получения данных о среднем росте первоклассников с заданной точность необходимо обследовать 52 школьника.
Ø Механическая выборка.
При решении задач на определение средней ошибки механической выборки, а также необходимой ее численности, следует использовать приведенные выше формулы, применяемые при собственно- случайном бесповторном отборе.
Ø Типическая выборка.
· Средняя ошибка выборки определяется по формулам:
(повторный отбор);
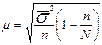(бесповторный отбор),
где 
- средняя из внутригрупповых дисперсий.
Например. В целях изучения доходов населения по трем районам области сформирована 2%- ная выборка, пропорциональная численности населения в этих районах. Полученные результаты представлены в табл.3.
Таблица 3
