Сущность метода заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3,5, 7 и т.д.), первых по счету уровней ряда, затем- из такого же числа уровней, но начиная со второго по счету, далее- начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок.
Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следовательно, потеря информации.
Например: Расчет скользящей средней по данным об урожайности зерновых культур:
Исходные данные и результаты расчета скользящей средней, ц/ га
| Год | Фактический уровень урожайности, ц | Скользящая средняя | |
| трехлетняя | пятилетняя | ||
| 15,4 | - | - | |
| 14,0 | 
| - | |
| 17,6 | 
| 14,7 | |
| 15,4 | 
| 15,1 | |
| 10,9 | 14,6 | 15,2 | |
| 17,5 | 14,5 | 17,1 | |
| 15,0 | 17,0 | 16,8 | |
| 18,5 | 15,9 | 17,6 | |
| 14,2 | 15,9 | - | |
| 14,9 | - | - | |
|
4. Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики.
Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:
,
где 
- уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Аналитическое выравнивание может быть:
· по прямой – используется в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней);
· по показательной функции – используется, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны.
«Техника» выравнивания ряда динамики по прямой:
.
Параметры 
, находятся решением следующей системы нормальных уравнений:
где у- фактические (эмпирические) уровни ряда;
t- время (порядковый номер периода или момента времени).
Расчет параметров упрощается, если за начало отсчета времени (t=0) принять центральный интервал (момент).
При четном числе уровней (например, 6) значения t – условного обозначения времени будут такими:
| 1995 г. | 1996 г. | 1997 г. | 1998 г. | 1999 г. | 2000 г. |
| -5 | -3 | -1 | +1 | +3 | +5 |
При нечетном числе уровней (например, 7) значения устанавливаются по –другому:
| 1994 г. | 1995 г. | 1996 г. | 1997 г. | 1998 г. | 1999 г. | 2000 г. |
| -3 | -2 | -1 | +1 | +2 | +3 |
В обоих случаях 
, так что система нормальных уравнений примет вид:
Из первого уравнения 
.
Из второго уравнения 
.
Например: рассмотрим выравнивание ряда динамики по прямой согласно примеру урожайности зерновых культур (см. выше).
Для выравнивания данного ряда уравнение прямой - , а n= 10 – четное число.
Вычислим параметры и .
Выравнивание по прямой ряда динамики
урожайности зерновых культур
| Год | t |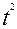 
| У*t |
|  
| ( ) 
|
| -9 | -138,6 | 15,15 | 0,25 | 0,0625 | ||
| -7 | -98,0 | 15,19 | -1,19 | 1,4161 | ||
| -5 | -88,0 | 15,23 | 2,37 | 5,6169 | ||
| -3 | -46,2 | 15,28 | 0,12 | 0,0144 | ||
| -1 | -10,9 | 15,32 | -4,42 | 19,5364 | ||
| +1 | 17,5 | 15,36 | 2,14 | 4,5796 | ||
| +3 | 45,0 | 15,40 | -0,40 | 0,016 | ||
| +5 | 92,5 | 15,45 | 3,05 | 9,3025 | ||
| +7 | 99,4 | 15,49 | -1,29 | 1,6641 | ||
| +9 | 134,1 | 15,53 | -0,63 | 0,3969 | ||
| Итого | 
| 
| 
|  =153,4
| 
| 
|
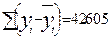
Из таблицы найдем:
,
откуда 
; 
.
Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: =15,34+ 0,021t.
Подставляя в данное уравнение последовательно значения t, равные -9, -7, -5, -3, -1, +1, +3, +5, +7, +9, находим выравненные уровни 
.
Если расчеты выполнены правильно, то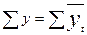 
. В примере 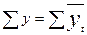=153,4. Следовательно, значения уровней выравненного ряда найдены верно.
Полученное уравнение показывает, что несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности: с 1986 по 1995 гг. урожайность зерновых культур в среднем возрастала на 
= 0,021 ц/ га в год.
Фактические и расчетные значения урожайности зерновых культур можно представить в виде графика:
Рис 1. Уровни урожайности зерновых культур:
эмпирические;
сглаженные по пятилетиям;
выравненые.
Соединив точки, построенные по фактическим данным, получим ломаную линию, на основании которой затруднительно вынести суждение о характере общей тенденции в изменении урожайности.
Тенденция роста урожайности зерновых культур в изученном периоде отчетливо проявляется в результате построения выравненной прямой
=15,34+ 0,021t.
5. При сравнении квартальных и месячных данных многих социально- экономических явлений часто обнаруживаются периодические колебания, возникающие под влиянием смены времен года.
В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезонные колебания» или «сезонные волны», а в динамический ряд называют сезонным рядом динамики.
Сезонные колебания обычно отрицательно влияют на результаты производственной деятельности, вызывая нарушения ритмичности производства.
В статистике существует ряд методов изучения и измерения сезонных колебаний. Самый простой заключается в построении специальных показателей, которые называются индексами сезонности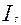 
. Совокупность этих показателей отражает сезонную волну.
Индексами сезонности являются процентные отношения фактических (эмпирических) внутригрупповых уровней к теоретическим (расчетным) уровням, выступающим в качестве базы сравнения.
Для того чтобы выявить устойчивую сезонную волну, индексы сезонности вычисляют по данным за несколько лет (не менее трех), распределенным по месяцам.
Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются по эмпирическим данным без их предварительного выравнивания.
Для каждого месяца рассчитывается средняя величина уровня, например за три года (
), затем вычисляется среднемесячный уровень для всего ряда 
. После чего определяется показатель сезонной волны – индекс сезонности 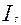как процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, %:
= 
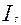*100,
где - средний уровень для каждого месяца (минимум за три года);
- среднемесячный уровень для всего ряда.
Для наглядного представления сезонной волны исчисленные индексы сезонности изображают в виде графика.
Например: имеются данные о производстве яиц по данным АО за три года, необходимо произвести расчет индексов сезонности.
