Вопросы:
1.Мода
2. Медиана
3.Понятие квартили, децили и перцентили
4. Децильные коэффициенты
5. Квартильные коэффициенты
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения признака. К таким показателям относится мода и медиана.
1. Мода- это значение признака, наиболее часто встречающееся в изучаемой совокупности.
Мода применяется, например, при определении размера одежды, обуви, пользующихся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар на рынке и т.д.
В дискретном ряду модой является вариант с наибольшей частотой (частостью).
Например:
Распределение рабочих по выработке деталей
| Выработка деталей за смену одним рабочим, шт. | Число рабочих (веса) |
| Итого |
Наибольшей частотой является число 5. Этой частоте соответствует модальное значение признака, т.е. выработка деталей за смену. Мода свидетельствует, что в данном примере чаще всего встречаются рабочие, изготавливающие за смену 20 деталей.
При расчете моды для интервального вариационного ряда необходимо вначале определить модальный интервал, в пределах которого находится мода, а затем значение модальной величины признака.
Модальный интервал- это интервал, имеющий наибольшую частоту (частость).
В интервальном вариационном ряду мода рассчитывается по формуле:
Мо= 
+h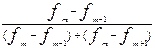 
где -нижняя граница модального интервала;
h- величина модального интервала;
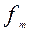- частота модального интервала;
- частота интервала, предшествующего модальному;
- частота интервала, следующего за модальным.
Например: имеются следующие данные обобщения итогов выборочного бюджетного обследования населения города Новосибирска:
| Среднедушевой денежный доход в среднем за месяц, тыс. руб. | Число жителей | Накопленные частости (S) | Середина интервала (х) | |
| чел. (f) | в % к итогу | |||
| До 0,5 | 0,9 | 0,9 | 0,25 | |
| 0,5-1,0 | 16,5 | 17,4 | 0,75 | |
| 1,0-1,5 | 24,6 | 42,0 | 1,25 | |
| 1,5-2,0 | 18,8 | 60,8 | 1,75 | |
| 2,0-2,5 | 15,4 | 76,2 | 2,25 | |
| 2,5-3,0 | 12,5 | 88,7 | 2,75 | |
| 3,0 и более | 11,3 | 100,0 | 3,25 | |
| Итого | 100,0 | - | - |
Модальное значение признака, используя в качестве весов частости распределения получим:
Мо= 1,0+0,5 
тыс. руб.
Таким образом, наиболее часто встречающаяся величина среднедушевого дохода составляет 1290 руб.
Расчет моды с использованием в качестве весов частот распределения дает аналогичный результат:
Мо=1,0+0,5 
тыс. руб.
Вычисление моды в интервальном ряду является весьма условным.
Мода и средняя величина по – разному характеризуют совокупность. Мода определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности.
Мода по своему обобщающему значению менее точна по сравнению со средней арифметической, характеризующей совокупность в целом с учетом всех без исключения элементов совокупности.
2. Медиана- это вариант, который находится в середине вариационного ряда.
Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы.
Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда.
В ряду, состоящем из 15 чисел, медианой будет 8-е число, от которого как вниз,так и вверх будет расположено по 7 чисел.
Например:
А: Дан нечетный вариационный ряд роста студенток:
156 158 160 161 166 168 172
Таким образом, центральным числом (медианой) данного ряда является рост студентки -161 см.
В случае четного вариационного ряда медиана определяется следующим образом: серединные два члена вариационного ряда складываются и делятся пополам.
В: Дан четный вариационный ряд роста студенток:
155 156 158 160 161 166 168 172
Ме= 
.
Если варианты в ряду распределения заданы в виде интервалов, то первоначально находят медиальный интервал, который содержит единицу, находящуюся в середине ранжированного ряда.
Медиальный интервал- это интервал, в котором находится порядковый номер медианы.
Медиана интервального ряда определяется по формуле:
Ме= 
,
где - нижняя граница медиального интервала;
i- величина медиального интервала;
- сумма накопленных частот в интервалах предшествующих медиальному;
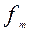- частота медиального интервала.
Например: В интервальном ряду даны группы семей по среднемесячному доходу на 1 человека. Требуется определить для этого ряда серединное значение, т.е. медиану.
| Группы семей по среднемесячному доходу на 1 человека, руб. | Число семей |
| До 900 | |
| 900-1200 | |
| 1200-1500 | |
| 1500-1800 | |
| Свыше 1800 | |
| Итого |
Ме=1200+300 
руб.
Следовательно, 50% семей имеют доход на одного человека 
1360 руб., а 50% имеют доход на одного человека > 1350 руб.
Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения.
3. Более общая постановка вариант, занимающих определенное порядковое место в ранжированном ряду, называется порядковой статистикой.
К порядковым статистикам принадлежат и экстремальные значения признака, т.е. минимальные и максимальные в данном ряду. Различают порядковые статистики, отсекающие четверти совокупности, которые называются квартили; в первую или нижнюю (отсекающие четверть совокупности снизу), третью или верхнюю (отсекающие четверть сверху). Второй квартилью можно назвать медиану. Далее можно говорить об отсекающих десятые части – децилях и т.д.
Определение этих порядковых статистик в вариационном ряду, так же как и определение медианы, начинается с расчета порядкового номера соответствующего варианта, а затем по накопленным частотам определяется интервал, в котором находится соответствующий вариант. Определение величины накопленного варианта внутри интервала тоже абсолютно аналогично нахождению медианы.
Таким образом, к структурным характеристикам относятся и другие порядковые статистики: квартили – делящие ряд на 4 равные части, децили- делящие ряд на 10 частей, перцинтили- на 100 частей и т.д.
4. Общая схема расчета децилей следующая:
1) поскольку децили отсекают десятые части совокупности, по накопленным частостям определим интервалы, куда попадают порядковые номера децилей: для первой децили - интервал, где находится вариант, отсекающий 10% совокупности с наименьшими значениями признака; для второй - 20% и т.д.; для девятой децили – интервал, содержащий вариант, отсекающий 90% с наименьшими значениями, или, что то же самое, 10% с наибольшими значениями признака;
2) Рассчитаем величину децилей по формулам.
Например, первая и девятая децили находятся по формулам:
;
= 
.
Где- , -начала интервалов, где находятся первая и девятая децили;
, 
- величина интервалов, где находятся первая и девятая децили;
- общая сумма частот (частостей);
, 
- суммы (частот (частостей), накопленных в интервалах, предшествующих интервалам, в которых находятся первая и девятая децили;
, 
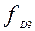-частоты (частости) интервалов, содержащих первую и девятую децили.
Например: согласно имеющихся данных об итогах выборочного бюджетного обследования населения города Новосибирска (см. пример выше) первая дециль попадает в интервал от 0,5 до 1,0 тыс. руб. (сумма накопленных в этом интервале частостей составляет 17,4%, что превышает 10%), девятая дециль – в интервал от 3,0 тыс. руб. и более (в этом интервале находится 10 % населения с наибольшими доходами). Найдем величину соответствующих децилей.
тыс. руб.
Следовательно, максимальная величина месячного среднедушевого дохода у 10% наименее обеспеченных жителей составила 776 руб.
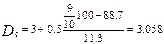тыс. руб.
Минимальная величина месячного среднедушевого дохода у 10% наиболее обеспеченного населения города составляла 3058 руб.
Соотношение децильных коэффициентов в социальной статистике получило название коэффициента децильной дифференциации доходов населения (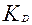
):
= 
.
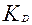В рассматриваемом примере:
3,9.
Это означает, что минимальный месячный среднедушевой доход 10% наиболее обеспеченного населения превышал максимальный доход 10% наименее обеспеченного населения в 3,9 раза.
5. Наряду с децилями применяются квартили.
Квартили- это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% между Q2 и Q3 и остальные 25% превосходят Q3.
В интервальном вариационном ряду квартили внутри определенного по накопленным частотам интервалам рассчитывается по следующим формулам:
Нижний квартиль:
Q1= +i 
.
Верхний квартиль:
Q3= +i 
,
Где х0 – нижняя граница квартильных интервалов;
i –величина интервала;
- сумма частот,
Sx1 – накопленная частота интервала, предшествующего нижнему квартилю;
Sx3 – накопленная частота интервала, предшествующего верхнему квартилю
- частота квартильного интервала.
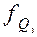
Если в качестве показателя центра распределения используется медиана, то Q2=Ме.
Например: В интервальном ряду распределения 50 учащихся по росту, определить верхний и нижний квартиль.
Распределение 50 учащихся по росту в интервальном ряду
| Рост, см х | Число учащихся | Накопленные частоты |
| 160-165 | ||
| 165-170 | ||
| 170-175 | ||
| 175-180 | ||
| 180-185 | ||
| 185-190 | ||
| 190-195 | ||
| Всего | - |
.
Следовательно, в ряду распределения по данным о распределении учащихся по росту первый квартиль составляет 170,8 см., а третий-180,8см, т.е. 25% учащихся имеют рост, не превышающий 170,8см., а у 75% учащихся рост не превышает 180,8 см.
Контрольные вопросы:
1. В чем сущность моды и как она рассчитывается для вариационного и интервального ряда?
2. Что такое медиана и как она рассчитывается для интервального ряда?
3. Что такое квартили, децили?
4. Как рассчитываются квартили?
5. Каков порядок расчета децили?
