Частотное распределение психографических признаков по группам акцентуаций характера

Психогра-

фические

признаки

1. Группа

(Pd)

2. Группа

(Pt)

3. Группа

(Sch)

 

В результате расчетов получены следующие величины коэф­фициента согласия Пирсона: χ²_1-2= 64.5; χ²₁ - ₃ = 96.5; χ²_{2 - 3} = 152.

Для определения значимости различий между выборками 1 и 2 необходимо войти в таблицу вероятностей Р для крите­рия χ² (Пирсона) (табл. 7). Число k (число степеней свободы) определяется с учетом количества переменных и в нашем слу­чае равно 17 (по горизонтали), а χ² равен 64.8 (по вертикали). При интерполяции табличных данных видно, что вероятность совпадения первого и второго распределений составляет ме­нее 0.01*.

* Прикладная математика. — М.: ВПА, 1986. — С. 125-129.

 

Таблица 7

Таблица вероятностей Р для критерия χ² (Пирсона)*

* На практике для определения критерия данного типа связи пользуются сужде­нием о вероятности совпадения признаков Р≤0.05. Но в книге А.И. Карасева «Основы математической статистики» (М.: Росвузиздат, 1962) на стр. 268 изложено названное выше правило: Р ≤ 0.01.

χ2/k
	0.1718	0.4159	0.7576	0.8912	0.9580	0.9921	0.9997	1.0000	1.0000
	0.0186	0.0752	0.2650	0.4405	0.6160	0.8197	0.9682	0.9967	0.9996
	0.0018	0.0104	0.0591	0.1321	0.2414	0.4514	0.7764	0.9414	0.9850
	0.0002	0.0013	0.0103	0.0293	0.0671	0.1719	0.4579	0.7468	0.8929
	0.0000	0.0001	0.0016	0.0053	0.0148	0.0499	0.2014	0.4624	0.6782
	0.0000	0.0000	0.0002	0.0009	0.0028	0.0119	0.0699	0.2243	0.4140

 

Вывод: частотные характеристики двух совокупностей (1 и 2) не имеют статистически значимой связи.

Аналогично рассчитываются характеристики остальных со­вокупностей переменных.

6) Для определения статистической связи переменных, из­меренных в дихотомической шкале наименований, использу­ются коэффициенты контингенции (Q) и ассоциации (Ф).

Вычисление значений а, b, с, и d осуществляется при помо­щи таблицы 8.

Таблица 8

 

 

	Признак А
А	не А
Признак В	В	а	b
не В	с	d

 

Пределы изменения значений коэффициентов Q и Ф нахо­дятся в интервале от —1 до +1.

Полученные в результате вычислений данные интерпрети­руются следующим образом: если значение Q и Ф равны 0, то связь отсутствует. Если значение Q и Ф по абсолютной величи­не больше 0.5, то связь между переменными сильная. Если ме­нее 0.5 — слабая. Знак коэффициента показывает направление изменений признаков, то есть при «-» зависимость связей об­ратная, а при «+» — прямая*.

* Прикладная математика. - М.: ВПА, 1986. — С. 125-129.

 

Практическое задание. Рассчитать статистическую связь между технической и гуманитарной направленностью школь­ников, измеренных в дихотомической шкале наименований по данным TAX и ДДО*.

* TAX — тест адекватных характеристик объекта; ДДО — дифференциально-ди­агностический опросник.

 

Эмпирические данные по результатам психодиагностики представлены в таблице 9.

 

Таблица 9

 

В результате проведенных расчетов получено:

Интерпретация:

1) признаки технической и гуманитарной направленности испытуемых, измеренные с помощью психологических методик TAX и ДДО, имеют сильную прямую статисти­ческую связь (по данным Q);

2) коэффициенты Q и Ф имеют разный уровень мощности. Так, коэффициент контингенции (Q) обладает меньшей мощностью, чем коэффициент ассоциации (Ф).

7) Для определения статистической связи переменных, из­меренных в порядковой шкале, используют коэффициент ран­говой корреляции Спирмена (R_s), который вычисляется по формуле:

Теоретическая интерпретация коэффициента ранговой корреляции Спирмена R_s идентична любой статистике из об­ласти измерения связей переменных. Если значение R_s более 0.5, то имеет место статистически сильная связь, если менее 0.5 — слабая. Положительные и отрицательные знаки пока­зывают направленность связи (соответственно, прямая и об­ратная).

Практическое задание. Произвести расчет корреляционной связи показателей эффективности деятельности операторов и уровня их интеллекта (по IQ), измеренных в ранговой шкале (табл. 10):

Таблица 10

 

№ п/п	Оценка успешности деятельности операторов	Значение коэффициента IQ операторов
		1.5
	2.5
	2.5
	5.5
	5.5	1.5

 

В результате расчетов получено: R_s = 0.97 (р < 0.05)*. Имеет место сильная положительная значимая на уровне (р < 0.05) связь переменных.

* См. доверительный интервал психологических измерений.

 

Вывод: успешность деятельности операторов определяется их уровнем интеллекта, измеренном в IQ.

Параметрическая статистика применяется в тех случаях, когда тестовые показатели измерены в интервальной шкале, шкале отношений или абсолютной шкале при соблюдении рас­пределения Гаусса. В данном случае применяются методы ана­лиза данных при помощи моды, медианы и среднего (М_о; М_е; М_х) [меры центральной тенденции], дисперсии и среднего квадратического отклонения (D_x; δ_х), коэффициента вариации (V) [меры изменчивости], коэффициента корреляции Пирсона (R_xy)[ меры связи], t-критерия Стьюдента, υ — критерия Уэлша, F-критерия Фишера [статистический вывод] и психодиаг­ностического прогнозирования при помощи методов линейной и нелинейной регрессии [модели регрессии].

Статистические методы применяются в определенном до­верительном интервале, который задается исходя из потребно­стей точности измерений. Доверительным интервалом называ­ется интервал (Х ± ε), который «накрывает» неизвестный пара­метр с заданной точностью. В биологических и социальных ис­следованиях максимальное значение ε задается в пределах 5%. То есть ε < 0.05.

8) Основной мерой центральной тенденции в параметричес­ком измерении является среднее значение — математическое ожидание (М_х). Это сумма всех измеренных значений свойства, отнесенное к количеству этих измерений.

где x_i — i -е значение свойства;

n — количество измерений.

 

9) Изменчивость признаков в параметрических шкалах из­меряется при помощи дисперсии и среднего квадратического отклонения (δ_x)*. Среднее квадратическое отклонение опреде­ляется как арифметическое значение квадратного корня из дис­персии — среднего арифметического квадратов отклонений отдельных значений измеренного свойства от их среднего зна­чения.

* Среднее квадратическое отклонение иногда обозначается в литературе как сред­неквадратичное отклонение или стандарт. См.: Прикладная математика. — М.: ВПА, 1986. — С. 122; Осипов Г.В., Андреев Э.П. Методы измерения в социологии. — М.: На­ука, 1977. - С. 74.

 

10) Коэффициент корреляции Пирсона (R_xy) показывает наличие статистической связи между психологическими пере­менными x и у, при которой каждой переменной х соответству­ет не одно или несколько определенных значений у, а распре­деление у, меняющееся вместе с изменением х, которое может быть однонаправленным (+) и разнонаправленным (-).

где х_i — значение показателя первой переменной;

у_i — значение показателя второй переменной;

N — объем выборки.

 

Теоретическая интерпретация коэффициента корреляции Пирсона R_xy подобна другим статистикам из области измере­ния связей между переменными. Если значение R_xy более 0.5, то имеет место статистически сильная связь, если менее 0.5 -слабая. Положительные и отрицательные знаки показывают направленность связи (соответственно, прямая и обратная).

Практическое задание. Рассчитать коэффициент корреляции Пирсона между показателями САД* и IQ, измеренных в шкале интервалов (табл. 11).

* САД — психодиагностическая методика «Семантический анализ деятельности».

 

 

Таблица 11

 

№ п/п	САД-оц	IQ-оц
	6
мх	5.8
δх	2.18	9.78
Аs	-0.26	-0.37
Ее	1.92	1.94

 

R_xy =0.84; р<0.05

Вывод: значения показателей двух тестов сильно связаны между собой. Корреляционная связь значима на уровне р<0.05.

 

11) При определенном количестве измерений (n) корреляци­онные связи могут быть значимыми и незначимыми. Исследова­телю необходимо это знать для того, чтобы сделать достоверный вывод о причинно-следственных связях переменных. Уровень значимости коэффициентов корреляции определяется по формуле расчета t-критерия при помощи таблиц «Квантилей t-распределения Стьюдента для доверительной вероятности» (см. табл. 12).

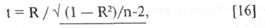
где R — численное значение коэффициента корреляции;

n — объем выборки.

 

Таблица 12