Эмпирические данные, полученные в результате исследования

 

№ п\п	xi	xi2	xi3	xi4
А	В	А	В	А	В	А	В
∑

 

1) Расчеты коэффициентов асимметрии и эксцесса.

2) Расчет дисперсий эмпирической оценки асимметрии и эксцесса.

Sa = 6*9/11*13= 54/143 =0.38;

Se = 240*8*7/121*13*15 =13140/23595 =0.56.

3) Исследование отклонений эмпирических данных от тео­ретической нормали (распределения Гаусса).

 

Согласно критериям П. Л. Чебышева:	Из практики профотбора:
а) по асимметрии: I As Группа А - 0 < 0.4 Группа В - 0.2 < 0.4	I As I < 2-3 Sa 0<1.14 0.21 < 1.14
б) по эксцессу: I Ex	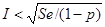I Еx I < 2-3 Se
Группа А - 0.94 > 0.59 Группа В - 0.97 > 0.59	0.94 < 1.68 0.97 < 1.68

 

4) Вывод о нормальности распределения эмпирических данных.

Распределение эмпирических данных имеет значимое отри­цательное смещение по вертикали. Это говорит о «плоском» профиле распределения признаков вокруг средних значений (дифференциация признаков) при соблюдении его симметрич­ности. В целом распределение близко к теоретической норма­ли. Измеренные свойства эмпирических переменных отража­ют свойства генеральной совокупности. Наблюдается относи­тельная дифференциация исследуемых признаков. В целом воз­можно применение методов параметрической статистики.

Оценка нормальности распределения эмпирических данных может осуществляться при помощи критерия согласия Пирсо­на* - Хи-квадрат (χ²), который вычисляется по формуле:

где n_i — частоты тестовых данных;

n_i⁰— теоретические частоты.

* О критериях согласия подробнее см.: Карасев А.И. Основы математической ста­тистики. — М.: Росвузиздат, 1962. — С. 265-278.

 

Определяется вероятность соответствия практической час­тоты проявления признака (по показателям теста) теоретичес­кому распределению (по специальным таблицам). Оценка рас­пределения по χ² на практике осуществляется при помощи ком­пьютера.

По результатам исследования параметров распределения эмпирических данных психолог может сделать по крайней мере два практических вывода:

Распределение тестовых данных близко (или нет) к нормаль­ному теоретическому распределению; следовательно, возмож­но применение методов параметрической статистики.

Тест хорошо (или слабо) дифференцирует испытуемых по структуре измеряемого свойства и в целом отражает (или нет) свойства изучаемой популяции.

Применение непараметрической и параметрической статистики при обработке эмпирических данных*

* См.: Суходольский Г.В. Основы математической статистики для психологов. — Л.: Изд-во ЛГУ, 1972; Гласc Дж., Стэнли Дж. Статистические методы в педагогике и пси­хологии. — М., 1976.

 

Методы непараметрической статистики применяются в тех случаях, когда показатели тестов распределены ненормально или распределение неизвестно. Существует определение: «Не­параметрические методы статистики — методы математической статистики, не предполагающие знание функционального вида генеральных распределений»*. Распространение методов непа­раметрической статистики сдерживается отсутствием учебных пособий по этому предмету. История непараметрических мето­дов начинается с использования критериев знаков Арбетноттом в 1710 г. Во второй половине XIX в. Фехнер и Гальтон стали применять ранги и коэффициенты ранговой корреляции. Работами Спирмена (1904) к ранговым методам было привлечено внимание научной общественности, а работы Колмогорова (1933), Смирнова (1935), Уилкоксона (1945), Сигеля (1956) и др. создали непараметрическую статистику как самостоятель­ную ветвь математической статистики.

* Математические методы анализа и интерпретация социологических данных. — М.: Наука, 1989. -С. 95-120.

 

Для определения статистических зависимостей в непарамет­рической статистике предназначены: мода (М_о), медиана (М_е), критерии Манна—Уитни, Уилкоксона, Хи-квадрат, коэффици­енты ассоциации (Ф) и контингенции (Q), преобразованный коэффициент корреляции Пирсона (j), коэффициенты сопря­женности Пирсона (С) (для больших выборок) и Чупрова (К) (для М × Н — клеточной сопряженности), коэффициент ран­говой корреляции Спирмена (R_s) и др.

В практической работе психологов и, в частности, в про­фотборе для статистической оценки связей эмпирических пе­ременных используют следующие коэффициенты:

а) в шкале наименований: коэффициент согласия Пирсона (x²), коэффициенты контингенции (Q) и ассоциации (Ф) (для 4-клеточной сопряженности), коэффициенты взаимной сопря­женности Пирсона (С) и Чупрова (К) (для m × n-клеточной со­пряженности).

 

б) в шкале порядков: коэффициент ранговой корреляции Спирмена (R_s).

Меры центральной тенденции:

1) Мода (М_о) — наиболее вероятное появление показателя.

2) Медиана (М_е) — вариант, приходящийся на середину ран­жированного вариационного ряда.

Меры связи и статистического вывода:

3) Критерий Манна—Уитни основан на парном сравнении результатов из первой и второй выборок.

4) Критерий Уилкоксона эквивалентен критерию Манна — Уитни и основан на переходе от наблюдений к их рангам.

5) Коэффициент согласия Пирсона (x²) основан на прибли­жении частоты проявления признака в различных выбор­ках, измеренного в номинальной шкале.

Расчет осуществляется по формуле:

где n_i¹ — частоты тестовых данных: частота (Р¹) проявления свойства у первого испытуемого;

n_i² — частоты тестовых данных: частота (Р²) проявления свойства у второго испытуемого.

В качестве примера рассчитаем величину коэффициента согласия Пирсона между группами испытуемых с акцентуа­циями характера [Pd (психопатия); Pt (психастения); Sch (шизоидность)] по величине проявления психографических при­знаков в рисунках испытуемых, которые измерены в процен­тах (%)*.

Вычислим коэффициент согласия Пирсона по проявлению психографических признаков в рисунках испытуемых экспе­риментальных групп, для чего воспользуемся данными, пред­ставленными в табл. 6.

* Данные из статьи Игнаткина В.Н., Носса И.Н. Исследование валидности графи­ческого теста Коха (рисунок дерева) // Психологическое обозрение. — № 2. — 1998. — С. 20-25.

 

Таблица 6