Цель урока: 1) перенести знания об умножении двузначного числа на двузначное на умножение любого многозначного числа на двузначное;
2) познакомить с отдельным случаем умножения многозначного числа на 11.
3) развивать навык устных и письменных вычислений;
4) снижать уровень тревожности на уроке;
5)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
4. Работа по учебнику
(У) Задания 9, 8, 2, 5*.
Задание 2. Обращаем внимание, как получены первое и второе неполные произведения. На какое число нужно умножить число 1537, чтобы получить то же число 1537?
На какое число нужно умножить число 2458, чтобы получить число 4916? И т. д.
Определяются вторые множители в примерах (11, 22, 33, 32).
Для проверки можно на доске выполнить умножение четвертого примера (найти ошибку во втором неполном произведении и в произведении).
Задание 5*. Требуемое произведение:
 |
Среди множителей — числа 2 и 5, произведение которых равно 10. На какое бы число мы не умножали 10, произведение будет оканчиваться на 0.
Задание 8. Вспоминается прием определения общего количества десятков (сотен): нужно справа закрыть одну (две) цифры и прочитать полученное число.
Задание 9. Пользуемся правилами: чтобы уменьшить число в 10, 100 раз, нужно в его записи справа отбросить один, два нуля; чтобы увеличить число в 10, 100 раз, нужно в его записи справа дописать один, два нуля.
5. Работа в тетрадях
(П) Задания 1, 3, 4, 6, 7.
Задание 1. Особенность устного умножения двузначного числа на 11: последняя цифра в произведении совпадает с последней цифрой первого множителя; следующая цифра — сумма цифр (или последняя цифра суммы), а первая цифра — это первая цифра первого множителя (или на 1 большее число, если сумма цифр
двузначная).
Особенность письменного умножения многозначного числа на 11: неполные произведения одинаковы, сложение их выполняется при смещении второго произведения на разряд влево.
Задание выполняется двумя способами: устно и письменно.
Задание 3. Это задача на пропорциональное деление. Например: купили по одинаковой цене несколько красных карандашей на сумму 420 р. и несколько зеленых на сумму 1050р., всего 7 карандашей. Сколько купили красных карандашей и сколько зеленых?
1) 1050+ 420 = 1470 (р.);
2) 1470: 7 = 210 (р.);
3) 1050:210 = 5 (к.);
4) 420:210 = 2 (к.).
Физкультминутка
Задание 6. Деление величин на число выполняется наиболее удобным способом. Например:
9м: 4 = 900см: 4 = (800 + 100): 4 = 200 + 25 = 225(см) = = 2 м 25 см.
Задание 7. х - 5 = 18; х = 23 (ящ.).
Д) Задания 10, 11.
Задание 10. 25 • 5 = 125 (пак.); 125 + 25 = 150 (пак.);
750: 150 = 5 (школ).
7. Подведение итогов урока
8. Рефлексия
Урок 108
Тема урока. Умножение на трехзначные числа.
Цели урока: 1) закрепить умножение многозначного числа на двузначное число;
2) перенести знания об умножении на двузначное число на умножение на трехзначное число.
3) развивать навык устных и письменных вычислений;
4) снижать уровень тревожности на уроке;
5)воспитывать интерес к урокам математики
Ход урока
1. Организационный момент
2. Проверка домашнего задания
3. Устный счёт
4. Работа по учебнику
(У) Задания 7, 6, 5, 8*.
Задание 5. На весах 600 г яблок и гиря 200 г, всего 800 г. Весы уравновешены. Значит, на каждой чаше по 400 г.
400 - 200 = 200 (г) — весят 4 маленьких яблока.
200: 4 = 50 (г) — весит одно маленькое яблоко.
Задание 6. Достаточно назвать несколько числовых значений букв. Числа определяются подбором или сведением неравенства к равенству. Например:
Х ∙ 6<90; х ∙ 6 = 90; х = 15;
неравенство будет истинным при х = 0, 1, 2, 3, 4,..., 14.
а:15>9 (160, 175,...);
400:с>40 (1, 2, 4, 5, 8);
х + 72<100 (0, 1, 2,..., 27).
Задание 7. Объяснение: 5 > 2; первое неполное делимое — 5 тыс. Значит, в частном будут разряды: тысячи, сотни, десятки, единицы — всего 4 цифры, и т. д.
5. Работа в тетрадях
(П) Задания 1, 2, 3, 4.
Задание 8*. 15 + 3 = 18 (м.);
18: 3 = 6 (м.) — у Сергея;
15-6 = 9 (м.) — у Андрея.
 |
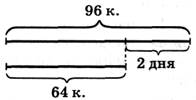Задание 2.
1) 96 - 64= 32 (к.) — на столько меньше раскрасил второй художник, чем первый;
2) 32: 2 = 16 (к.) — выработка за день каждого художника;
3) 96:16= 6 (дней) — работал первый художник;
4)64: 16= 4 (дня) — работал второй художник.
Задачу можно решить другими способами.
Например: за 2 дня каждый из художников может раскрасить 32 кувшина. (96 - 64 = 32.)
Тогда для раскраски 96 кувшинов понадобится в 3 раза больше дней, а для раскраски 64 кувшинов — в 2 раза больше дней (6 дней и 4 дня).
Физкультминутка
Задание 3. 19 075; 50; 290; 54 060.
Задание 4.
S1 = 8 ∙ 6 = 48 (см2); S2 = 4 • 12 = 48 (см2); S, = S2.
Р1 = 2 ∙ (8 + 6) = 28(см); Р2 = 2 • (4 + 12) = 32 (см); Р 1 < Р2.
Д) Задания 9, 10.
Задание 9.
(1750 + 1350) ∙ 60 = 3100 • 60 = 186 000 (г) = 186 кг;
1750 • 60 + 1350 • 60 = 105 000 + 81 000 = 186 000 (г) = 186 кг.
Задание 10. 240 856 655 290 1 309 671
84 183 3 987 032 1 070 840
7. Подведение итогов урока
8. Рефлексия
Урок 109
