КЛАССИЧЕСКАЯ СТАТИСТИЧЕСКАЯ ФИЗИКА
Основные положения
Объект – идеальный газ частиц, подчиняющихся классической механике и описываемых уравнениями Гамильтона. Эти уравнения являются законами динамики, выраженными через гамильтониан – полную энергию системы.
Задача – найти статистические распределения частиц общим числом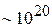 
по координатам, импульсам, энергии. Используется метод, разработанный Гиббсом в 1902 г.
Джозайя Уиллард Гиббс (1839–1903)
Основные понятия – микросостояние системы, макросостояние системы, фазовое пространство, функция распределения по фазовому пространству.
Микросостояние системы – совокупность координат и импульсов всех частиц, зафиксированных в один момент времени. Отображается точкой X фазового пространства. С течением времени точка перемещается по этому пространству.
Функция распределения в фазовом пространстве. Чем чаще точка появляется в мысленно выделенном единичном объеме около X, тем больше плотность вероятности 
, то есть функция распределения.
Статистический интеграл Z – нормировочная постоянная распределения.
Макросостояние системы – состояние газа, описываемое термодинамическими величинами – температурой Т, давлением Р, внутренней энергией U, свободной энергией F и др. Одно макросостояние реализуется множеством разных микросостояний, образующих фазовый ансамбль. Термодинамическая величина, характеризующая макросостояние, получается усреднением по фазовому ансамблю с использованием функции распределения, и выражается через статистический интеграл Z.
Фазовое пространство системы частиц
Микросостояние системы отображается точкой фазового пространства
,
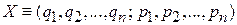где 
и 
– обобщенные координаты и импульсы частицы системы; n – число степеней свободы системы, пропорциональное числу частиц. Число независимых координат фазового пространства равно 2 n. Для каждой системы используется свое фазовое пространство.
Координата частицы газа и ее импульс с течением времени изменяются согласно уравнениям Гамильтона
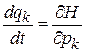, (2.1а)
. (2.1б)
Уильям Гамильтон (1805–1865)
Гамильтониан – полная энергия системы в виде суммы кинетических и потенциальных энергий всех частиц, выраженная через координаты и импульсы частиц:
,
где
.
Для консервативной системы полная энергия сохраняется
,
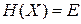и микросостояния находятся на гиперповерхности фазового пространства.
Уравнения Гамильтона для одномерного движения частицы. Гамильтониан складывается из кинетической и потенциальной энергий
.
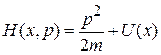Из (2.1а) 
получаем
,
из (2.1б)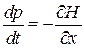 
находим
.
Первое уравнение связывает скорость с импульсом и является формулой кинематики, второе – вторым законом Ньютона. Уравнения Гамильтона являются унифицированной формой записи известных уравнений механики.
Число степеней свободы
Число степеней свободы системы n равно сумме степеней свободы составляющих частиц. Если есть N одинаковых частиц и у каждой f степеней свободы, то
.
Число степеней свободы частицы f есть число независимых координат, определяющих ее положение в пространстве. Изменение координаты означает движение, тогда f – число независимых видов движений.
Атом, рассматриваемый как материальная точка, имеет в трехмерном пространстве координаты (x,y,z) и 
. Изменение координат дает три независимых поступательных движения вдоль декартовых осей. Вращательные движения не изменяют координат.
Двухатомная молекула. Два атома имеют 6 координат. Если между атомами жесткая связь длиной l, тогда координаты связаны теоремой Пифагора – одним уравнением
.
Независимыми являются 
координат. Их изменение дает 3 поступательных и 2 вращательных движения вокруг осей x и z. Вращение вокруг оси y не изменяет координаты атомов.
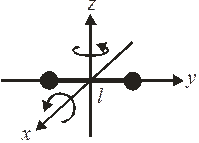
Если связь между атомами упругая, то атомы колеблются относительно друг друга, и добавляются 2 степени свободы – кинетическая и потенциальная энергии колебаний, тогда 
.
N-атомная молекула. Атомы имеют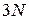 
координат, часть из них зависит друг от друга благодаря связям между атомами. Найдем число видов движений.
При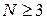 
число степеней свободы молекулы:
3 степени свободы – поступательные движения вдоль трех декартовых координат;
3 степени свободы – вращения вокруг трех осей координат;
если связи жесткие, то 
;
число связей между атомами 
;
если связи упругие, то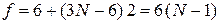 
.
Например, для 
получаем 
.
