В процессе освоения материала Вы должны выполнить задание на практическое занятие №6 и задание №3 контрольной работы.
Изучение экономических и социальных явлений и процессов предполагает анализ взаимосвязи между ними (например, выпуск продукции зависит от производительности труда работников, объем продаж от числа покупателей и т. д.). Формы проявления взаимосвязей очень разнообразны (рис. 3.2.1). В качестве двух самых общих обычно выделяют функциональную и корреляционную (статистическую) связи.
| По силе связи: ¾ сильные ¾ слабые |
| Формы взаимосвязей |
| По характеру: ¾ функциональные (точные, жесткие 100%-ные) – каждому значению аргумента соответствует только одно значение функции ¾ вероятностные (статистические, корреляционные проявляются в среднем, для массовых наблюдений) – каждому значению аргумента соответствует некоторое множество вероятных значений функции |
| По направлению: ¾ прямые – зависимая переменная возрастает с увеличением факт. признака ¾ обратные – рост факт. признака сопровождается уменьшением функции |
| По аналитической форме: ¾ линейные – переменные связаны линейной функцией (прямая зависимость) ¾ нелинейные – переменные связаны нелинейно (параболическая, экспоненциальная, гиперболическая и др. зависимости) |
| По количеству взаимодействующих факторов: ¾ парные – изучается связь двух признаков ¾ множественные – изучается зависимость между системами признаков |
Рис. 3.2.1. Формы взаимосвязей
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие.
Основными методами изучения функциональных связей являются:
1) балансовый,
2) индексный (см. тему 2.2).
Статистический баланс представляет собой систему показателей, которая состоит из двух сумм абсолютных величин, связанных знаком равенства:
А + В = D + Е
Например, балансовая модель движения оборотных средств выглядит следующим образом:
Остаток начальный + Поступление – Расход = Остаток конечный
Для изучения статистических взаимосвязей применяются две группы методов:
1) корреляционный анализ,
2) регрессионный анализ.
Иногда эти методы объединяют в единый корреляционно-регрессионный анализ (КРА).
Корреляционный анализ изучает тесноту связи между показателями, т.е. как сильно зависит результативный показатель от факторного. При этом вводятся специальные характеристики, например, линейный коэффициент корреляции.
В теории регрессионного анализа изучается форма связи между показателями. При этом полученные эмпирические данные аппроксимируются известными математическими функциями. В простейшем случае с помощью линейного уравнения.
Методы оценки тесноты связи подразделяются на два вида:
§ параметрические (корреляционные);
§ непараметрические (анализ нечисловой информации).
Параметрические методы основаны на использовании оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является простота вычислений.
Когда имеют место двумерные данные, их можно изобразить на плоскости корреляции. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи.
На рисунке 3.2.2, составленном по данным таблицы, показаны две эмпирические линии регрессии:
¾ одна из них (сплошная линия) иллюстрирует изменение среднего уровня оплаты труда по мере увеличения производственного стажа;
¾ другая (пунктирная линия) – показывает средний стаж работы при данном уровне оплаты труда.
| Теоретическая линия регрессии |
| Эмпирическая линия регрессии |

0 0.5 1 1.5 2 2.5 3 3.5 Производственный стаж (лет)
Рис.3.2.2. Эмпирическая и теоретическая линии регрессии
Из графика видно, что чем больше производственный стаж, тем выше оплата труда. Такая диаграмма называется диаграммой рассеяния (эмпирической линией регрессии), и ее можно сгладить прямой линией. Сглаживающая (аппроксимирующая) прямая называется теоретической линией регрессии.
При статистическом исследовании корреляционных связей одной из основных задач является определение их формы, т.е. построение модели связи.
Построение регрессионной модели проходит несколько этапов:
1) сбор и подготовка информации,
2) выбор модели связи,
3) оценка показателей тесноты корреляционной связи,
4) оценка адекватности регрессионной модели.
Корреляция между случайными переменными величинами x и y называется линейной, если описывается линейным уравнением.
Линейное корреляционное уравнение прямой регрессии:

Параметр b – это коэффициент регрессии, характеризующий влияние, которое оказывает изменение x на y. Он показывает, на сколько единиц в среднем изменится y при изменении x на одну единицу.
Если b> 0, то наблюдается положительная связь (x ® y ).
Если b< 0, увеличение x на единицу приводит к уменьшению y в среднем на b (x ® y ¯).
Параметр b обладает размерностью отношения y к x.
Параметр а – это постоянная величина в уравнении регрессии ( начальное значение y). Интерпретируется только знак при свободном члене.
Если a >0, то вариация результата меньше вариации факторного признака.
Если a < 0, то вариация результата больше вариации факторного признака.
Например, по данным о стоимости оборудования x и производительности труда y получено уравнение:
y = -12,14 + 2,08 x.
Коэффициент b, означает, что увеличение стоимости оборудования на 1 единицу ведет в среднем к росту производительности труда на 2.08 единиц.
Так как a > 0, то вариация результата меньше вариации факторного признака.
Для количественной оценки степени связи между x и y используются следующие статистические показатели:
1. Линейный коэффициент корреляции (r).
Если заданы значения переменных x и y, для расчета линейного коэффициента корреляции используются формулы:


где
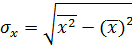


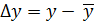
Свойства коэффициента корреляции:
1) абсолютные значения коэффициента корреляции не превосходят единицы:
-1 ≤ r ≤ 1
-1 ≤ r ≤ 0 – обратная связь 0 ≤ r ≤ 1 – прямая связь
2) чем ближе  к 1, тем теснее корреляция между х и у.
к 1, тем теснее корреляция между х и у.
Принято считать, что если:
|r|< 0,30, то связь слабая;
|r|= (0,3÷0,7) – средняя;
|r|> 0,70 – сильная, или тесная;
|r|= 1 – связь функциональная (линейная);
|r| » 0 – отсутствие линейной связи между x и y (возможны нелинейные связи).
2. Индекс корреляции (R):


Изменяется в пределах: 0 ≤ R ≤ 1
3. Корреляционное отношение (η):

Изменяется в пределах: 0 ≤ η ≤ 1
4. Коэффициент детерминации (η²).






