В данном разделе рассматриваются две темы:
2.1. Метод средних величин и вариационный анализ
2.2. Индексы и их применение в экономике
В процессе освоения материала Вы должны выполнить задания на практические занятия №3 и №4. Для студентов заочной формы обучения с элементами ДОТ практические занятия проводятся на форуме учебного сайта СЗТУ. После изучения учебного материала Вам необходимо ответить на вопросы самопроверки, приведенные в конце каждой темы, задание №1 контрольной работы и сделать тест №2.
Метод средних величин и вариационный анализ
Средняя величина является обобщающей характеристикой совокупности единиц по качественно однородному признаку.
Средние величины делятся на два больших класса (рис.2.1.1):
§ степенные средние,
§ структурные средние.
| Средние величины |
| Структурные § мода § медиана § квартили § квантили § децили |
| Степенные § Средняя гармоническая § Средняя геометрическая § Средняя арифметическая § Средняя квадратическая § Средняя кубическая |
Рис. 2.1.1. Виды средних величин
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Простая средняя рассчитывается по не сгруппированным данным и имеет следующий общий вид:
 ,
,
где Xi – значение осредняемого признака;
m – показатель степени средней;
n – число единиц признака.
Взвешенная средняя рассчитывается по сгруппированным данным и имеет общий вид:
 ,
,
где Xi – значение осредняемого признака;
m – показатель степени средней;
fi – частота, показывающая, сколько раз встречается i -тоe значение осредняемого признака.
Общие формулы расчета степенных средних имеют показатель степени m. В зависимости от того, какое значение он принимает, различают следующие виды степенных средних (таблица 2.1.2).
Таблица 2.1.2.
Виды степенных средних
| Вид степенной средней | Показатель степени (m) | Формула расчета | |
| Простая | Взвешенная | ||
| Гармоническая | -1 | 
| 
|
| Геометрическая | 
| 
| |
| Арифметическая | 
| 
| |
| Квадратическая | 
| 
| |
| Кубическая | 
| 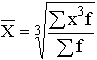
|
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

В статистической практике чаще, чем остальные виды средних, используются средние арифметические и средние гармонические взвешенные.
Пример. Расчет среднего возраста студентов в группе из 20 человек.
Таблица 2.1.3
| № п/п | Возраст (лет) | № п/п | Возраст (лет) | № п/п | Возраст (лет) | № п/п | Возраст (лет) |
| 1 2 3 4 5 | 18 18 19 20 19 | 6 7 8 9 10 | 20 19 19 19 20 | 11 12 13 14 15 | 22 19 19 20 20 | 16 17 18 19 20 | 21 19 19 19 19 |
Средний возраст студентов по формуле средней простой:

Сгруппировав исходные данные (таблица 1.5.2.), получаем новый показатель – частоту, показывающую число студентов в возрасте Х лет.
Таблица 2.1.4
| Возраст, Х лет | Всего | |||||
| Число студентов |
Следовательно, средний возраст студентов группы можно рассчитать по формуле средней взвешенной:

Структурные средние применяются для изучения внутреннего строения рядов распределения, а также для оценки средней величины, если по имеющимся статистическим данным ее расчет не может быть выполнен.
В качестве структурных средних чаще всего используют показатели моды и медианы.
Мода – значение показателя, которое чаще всего встречается в выборочных данных. Мода близка к среднему значению. Для дискретных рядов распределения модой является вариант с наибольшей частотой.
Медиана – показатель, приходящийся на середину вариационного ряда и делящий его на 2 равные части (по числу членов ряда n/2).
Наряду со структурными средними модой и медианой, на практике используют и другие показатели структуры, например, децили, квантили и квартили.
Квартили – значения показателя в ранжированном ряду, делящие этот ряд на 4 части (по 25% единиц совокупности).
Квантили делят ранжированный ряд на 5 частей (по 20% единиц совокупности).
Децили делят ранжированный ряд на 10 частей (по 10% единиц совокупности).
По данным структурным характеристикам рассчитывается статистический показатель – коэффициент фондовой дифференциации:
 ;
;
ДN - значение децили требуемого номера,
Д1 – значение первой децили.
Конкретные условия, в которых находится каждый из изучаемых объектов и особенности их развития выражаются различными числовыми значениями статистических показателей.
Вариация – несовпадение, отклонение значения одного и того же показателя у разных объектов.
Для измерения степени отклонения отдельных значений признака от их среднего значения в статистике используют абсолютные и относительные показатели.
Абсолютные показатели вариации:
1. Размах вариации (R) – разница между максимальным (Xmax) и минимальным (Xmin) наблюдаемыми значениями признака:
R = Xmax - Xmin
2. Среднее линейное отклонение (СЛО,  ) – среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
) – среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:

3. Дисперсия признака ( s²) – средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической.
В зависимости от исходных данных вычисляется по формуле средней арифметической простой или средней арифметической взвешенной:

4. Среднее квадратичное отклонение (СКО, s,s) – представляет собойквадратный корень из дисперсии.
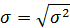

Для характеристики меры рассеивания изучаемого признака исчисляются относительные показатели рассеивания. Они позволяют сравнивать характер рассеивания в различных распределениях.
Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
1. Коэффициент осцилляции  отражает относительное отклонение крайних значений признака вокруг средней
отражает относительное отклонение крайних значений признака вокруг средней
 .
.
2. Относительное линейное отклонение  характеризует долю усредненного значения признака абсолютных отклонений от средней величины
характеризует долю усредненного значения признака абсолютных отклонений от средней величины

3. Коэффициент вариации (  :
:

По величине коэффициента вариации можно судить о степени вариации признаков, и, следовательно, об однородности изучаемой совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.
В статистике совокупности, имеющие коэффициент вариации больше 30–35%, принято считать неоднородными.
Если вариация оценивается по небольшому числу наблюдений, взятых их неограниченной генеральной совокупности, то среднее значение признака определяется с некоторой погрешностью.
Предположим, что в результате выборочных наблюдений мы получили ряд значений некоторой величины (некоторого признака):
x1, x2, x3,... xn.
Этот ряд значений величины x получил название выборки.
Характеристикой выборочной совокупности является выборочная средняя  . Она отличается от генеральной средней
. Она отличается от генеральной средней  на величину ошибки выборки Δx:
на величину ошибки выборки Δx:

Так как оценочные значения выборочной средней  и ошибки выборки Δx не являются точными, запись результата измерений должна сопровождаться указанием его надежности (доверительной вероятности) P.
и ошибки выборки Δx не являются точными, запись результата измерений должна сопровождаться указанием его надежности (доверительной вероятности) P.
Под надежностью или доверительной вероятностью (P) понимают вероятность того, что истинное значение измеряемой величины заключено в указанном интервале. Сам этот интервал называется доверительным интервалом.
Задача определения результата наблюдения, его ошибки и надежности решается с помощью теории вероятностей и математической статистики. В большинстве случаев случайные ошибки подчиняются нормальному закону распределения Гаусса.
При обработке выборочных наблюдений предлагается следующий порядок операций:
1. Вычисляется среднее значение выборки (из n наблюдений)
 .
.
2. Находится погрешность каждого отдельного значения

3. Вычисляются квадраты погрешностей отдельных значений
(Δx1)2, (Δx2)2,..., (Δxn)2.
4. Определяется дисперсия

5. Рассчитывается средняя ошибка выборки.
для случайного повторного отбора:

для случайного бесповторного отбора:

6. Задается значение надежности (обычно берется P = 0.95).
7. Определяется коэффициент Стьюдента t для заданной надежности P и числа наблюдений n.
8. Находится доверительный интервал (предельная ошибка выборки)
Δx = t·μ
9. Окончательный результат записывается в виде

10. Оценивается относительная погрешность результата измерений
 .
.
Вопросы для самопроверки по теме 2.1.
1. Какие виды средних величин используются в экономическом анализе?
2. Способы определения структурных средних (моды и медианы)?
3. В чем заключается смысл коэффициента вариации?
4. Перечислите основные этапы обработки результатов статистического наблюдения.
5. Что такое доверительная вероятность?






