Биномиальное распределение
Для построения контрольных карт (КК) числа и доли дефектных единиц (пр - и р - карты), а также для выбора планов контроля по альтернативному признаку за основу принимается биномиальное распределение.
Биномиальное распределение – распределение вероятностей дискретной случайной величины Х, принимающей любые целые значения от 0 до n, такие, что
Р 
(13)
при х = 0,1,2…, n и параметрах n = 1,2…;
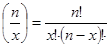(14)
где Р – вероятность обнаружить х несоответствующих единиц в выборке; n - объем выборки; р – вероятность обнаружить несоответствующее изделие.
Биномиальное распределение отличается следующими свойствами:
а) распределение является дискретным;
б) средним арифметическим биномиального распределения служит пр, а стандартным отклонением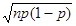 
;
в) если 
, а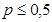 
, то в качестве приближения для биномиального предпочтительно в основном использовать нормальное распределение;
г) когда рассматривается доля несоответствующих изделий в выборке n, то необходимо вместо х брать 
, среднее арифметическое p, астандартное отклонение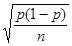 
.
Распределение Пуассона
Для построения контрольных карт числа и доли несоответствий (с - и u - карты) и проведения выборочного контроля по альтернативному признаку при малом проценте несоответствующих единиц и большом объеме выборки используют распределение Пуассона (распределение редких событий).
Если п стремится к бесконечности, то из биномиального распределения получают формулу Пуассона для выражения вероятности появления редких событий.
Распределение Пуассона – распределение вероятностей дискретной случайной величины Х такое, что
(15)
при х = 0,1,2…и параметре m >0, где m = пр.
Характерные свойства распределения Пуассона:
а) распределение Пуассона является дискретным;
б) среднее значение распределения Пуассона равно m, а стандартное отклонение 
.
Контрольные вопросы
1 Что значит случайная величина?
2 В чем различие между дискретной и непрерывной случайными величинами?
3 Что значит распределение вероятностей, функция распределения, плотность распределения?
4 Какие параметры характеризуют нормальный закон распределения?
5 Как изменится вид интегральной и дифференциальной кривой нормального распределения с изменением m и s?
6 Что такое нормирование?
7 Как с использованием функции нормированного нормального распределения определить значения функции и плотности нормального распределения?
8 Назовите свойства биномиального распределения.
9 Назовите свойства распределения Пуассона.
