В теории вероятностей рассматривается достаточно большое количество разнообразных законов распределения. Для решения задач, связанных с построением контрольных карт, представляют интерес лишь некоторые из них. Важнейшим из них является нормальный закон распределения, который применяется для построения контрольных карт, используемых при контроле по количественному признаку, т.е. когда мы имеем дело с непрерывной случайной величиной. Нормальный закон распределения занимает среди других законов распределения особое положение. Это объясняется тем, что, во-первых, наиболее часто встречается на практике, и, во-вторых, он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Что касается второго обстоятельства, то в теории вероятностей доказано, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, могут быть представлены как сумма весьма большего числа сравнительно малых слагаемых - элементарных ошибок, каждая из которых вызвана действием отдельной причины, независящей от остальных. Нормальный закон проявляется в тех случаях, когда случайная переменная Х является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину Х влияет незначительно, и нельзя указать, какой именно влияет в большей степени, чем остальные.
Нормальное распределение (распределение Лапласа–Гаусса) – распределение вероятностей непрерывной случайной величины Х такое, что плотность распределения вероятностей при - ¥ <х< + ¥ принимает действительное значение:
 ехр
ехр  (3)
(3)
То есть, нормальное распределение характеризуется двумя параметрами m и s, где m - математическое ожидание; s- стандартное отклонение нормального распределения.
Величина s 2 – это дисперсия нормального распределения.
Математическое ожидание m характеризует положение центра распределения, а стандартное отклонение s (СКО) является характеристикой рассеивания (рис. 3).
f(x) f(x)
 |
Рисунок 3 – Функции плотности нормального распределения с:
а) разными математическими ожиданиями m; б) разными СКО s.
Таким образом, значением μ определяется положением кривой распределения на оси абсцисс. Размерность μ - та же, что и размерность случайной величины X. С ростом математического ожидания mобе функции сдвигается параллельно вправо. С убывающей дисперсией s 2 плотность все больше концентрируется вокруг m, в то время как функция распределения становится все более крутой.
Значением σ определяется форма кривой распределения. Поскольку площадь под кривой распределения должна всегда оставаться равной единице, то при увеличении σ кривая распределения становится более плоской. На рис. 3.1 показаны три кривые при разных σ: σ1 = 0,5; σ2 = 1,0; σ3 = 2,0.
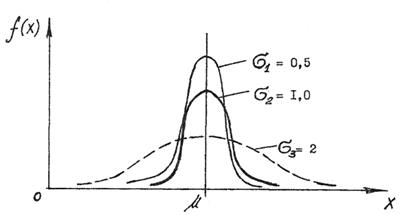
Рисунок 3.1 – Функции плотности нормального распределения с разными СКО s.
Функция распределения (интегральная функция) имеет вид (рис. 4):

 (4)
(4)
Рисунок 4 – Интегральная (а) и дифференциальная (б) функции нормального распределения
Особенно важно то линейное преобразование нормально распределенной случайной переменной Х, после которого получается случайная переменная Z с математическим ожиданием 0 и дисперсией 1. Такое преобразование называется нормированием:
 (5)
(5)
Его можно провести для каждой случайной переменной. Нормирование позволяет все возможные варианты нормального распределения свести к одному случаю: m = 0, s = 1.
Нормальное распределение с m = 0, s = 1 называется нормированным нормальным распределением (стандартизованным).
Стандартное нормальное распределение (стандартное распределение Лапласа–Гаусса или нормированное нормальное распределение) – это распределение вероятностей стандартизованной нормальной случайной величины Z, плотность распределения которой равна:
 ехр
ехр 
 (6)
(6)
при - ¥ < z < + ¥
Значения функции Ф(z) определяется по формуле:
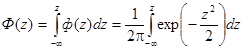 (7)
(7)
Значения функции Ф(z) и плотности ф(z) нормированного нормального распределения рассчитаны и сведены в таблицы (табулированы). Таблица составлена только для положительных значений z поэтому:
Ф ( – z) = 1 – Ф (z) (8)
С помощью этих таблиц можно определить не только значения функции и плотности нормированного нормального распределения для заданного z, но и значения функции общего нормального распределения, так как:
 ; (9)
; (9)
 . 10)
. 10)
Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины Х, подчиненной нормальному закону с параметрами m и s, на определенный участок. Таким участком может быть, например, поле допуска на параметр от верхнего значения U до нижнего L.
Вероятность попадания в интервал от х 1 до х 2можно определить по формуле:
 (11)
(11)
Таким образом, вероятность попадания случайной величины (значение параметра) Х в поле допуска определяется формулой
 (12)
(12)
Можно найти вероятность того, что случайная переменная Х окажется в пределах μ  k s. Полученные значения для k =1,2 и 3 следующие (также смотрим рис. 5):
k s. Полученные значения для k =1,2 и 3 следующие (также смотрим рис. 5):
 |
Рисунок 5 – Нормальный закон распределения
Между 3 σ-границами (μ -3 σ;μ +3 σ) находится 99,73% всех наблюдений, т. е. практически все значения. Только 0,27% значений находятся за этими границами, а именно 0,135% за границей μ +3 σ и 0,135% – за μ -3 σ:
| Границы | Число наблюдений между границами, % |
| μ–s, μ+s μ– 2 s, μ+ 2 s μ– 3 s, μ+ 3 s | 68,26 95,44 99,73 |
Таким образом, если какое-либо значение появляется за пределами трехсигмового участка, в котором находятся 99,73% всех возможных значений, а вероятность появления такого события очень мала (1:270), следует считать, что рассматриваемое значение оказалось слишком маленьким или слишком большим не из-за случайного варьирования, а из-за существенной помехи в самом процессе, способной вызывать изменения в характере распределения.
Участок, лежащий внутри трехсигмовых границ, называют также областью статистического допуска соответствующей машины или процесса.






