Рассмотрим алгоритм обратного распространения ошибки для адаптивных сетей (рис.2.46). Напомним, что сеть имеет L слоев (l =0,1,…, L) и l = 0 представляет входной слой. Слой l имеет N (l) вершин. Выходное значение вершины зависит от входных значений и параметров функции активации вершины. Обозначим выход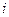 
-той вершины слоя 
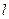как 
.
,
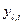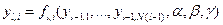где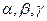 
- параметры функции активации 
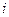-той вершины слоя .
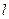Обучение методом обратного распространения ошибки в такой сети связано с настройкой параметров сети (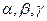) таким образом, чтобы ошибка на выходе была минимальной.
Предположим, что имеются P обучающих пар. Для входной обучающей пары p (p = 1,2,...,P) определим меру ошибки следующим образом:
, (2.23)
где
есть k -ая компонента вектора желаемого выхода для входного вектора p,
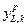- k -ая компонента вектора реального выхода для входного вектора p, 
- число выходных вершин.
Введем сигнал ошибки 
, связанной с выходом 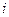-той вершиной слоя 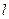, как производную от меры ошибки:
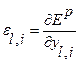
Сигнал ошибки 
, связанной с выходом 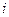-той вершиной выходного слоя L, вычисляется как
Используя (2.23), имеем:
.
Сигнал ошибки , связанной с выходом 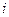-той вершины промежуточного слоя 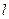, зависит от сигнала ошибки (l +1) слоя и от производной функции активации нейронов слоя (l +1). Таким образом, сигнал ошибки может быть вычислен следующим образом:
(2.24)
Для процесса обучения, связанного с настройкой параметров сети 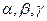, также будем использовать градиентный метод. Определим градиентный вектор как производную меры ошибки от параметров. Если 
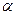- параметр функции активации 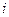-той вершины слоя 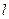, то, используя (2.24), то можем представить градиент ошибки по отношению к данному параметру как:
(2.25)
Далее, суммируя по всем обучающим парам, получим суммарную величину градиентов ошибки:
.
Теперь можем написать следующее правило обновления (обучения) параметров сети: на каждой следующей итерации алгоритма обучения добавлять к параметру 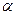его поправку в виде:
,
где 0 < η < 1 - множитель, задающий скорость обучения.
Заключительная дискуссия
1. В данном параграфе мы рассмотрели основной алгоритм обучения, используемый во многих задачах, где есть супервизорное обучение. Для задач управления мы также будем использовать этот алгоритм в составе общего инструментария проектирования ИСУ.
2. На каждой итерации алгоритма обратного распространения параметры нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации. Следовательно, проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров может быть много, адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.
3. Несмотря на многочисленные успешные применения метода обратного распространения ошибки, оно не является панацеей. В сложных задачах для обучения сети могут потребоваться длительное время, она может и вообще не обучиться. Причиной может быть одна из описанных ниже проблем.
4. В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях выходов, в области, где производная меры ошибки очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть (так называемый «паралич сети»). В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Кроме того, для предохранения от паралича или для восстановления после него используются различные эвристики.
5. Метод обучения на основе обратного распространения ошибки использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Другие методы (в частности ГА) обучения могут помочь избежать этой ловушки, но при большом объеме параметров они могут быть медленными.
6. Следует также отметить возможность переобучения сети, что является скорее результатом ошибочного проектирования её топологии. При слишком большом количестве нейронов теряется свойство сети обобщать информацию. Весь набор образов, предоставленных к обучению, будет выучен сетью, но любые другие образы, даже очень похожие, могут быть классифицированы неверно.
