–ассмотрим применение √ј в задачах интеллектуального управлени€.
ѕример 1. ѕрименение √ј дл€ оптимального выбора нечетких правил.
«адача 1 Ц парковка движущегос€ объекта.
–ассмотрим следующую задачу управлени€ движением тележки (рис.2.29): разработать нечеткий регул€тор (Ќ–), который переводит тележку (объект управлени€ - ќ”) из заданных начального положени€ и начальной скорости в целевое положение (0,0) (центровка и останов) за минимальное врем€.
Ќачальное состо€ние ќ”:  ; ÷елевое (конечное) состо€ние ќ”: [0,0].
; ÷елевое (конечное) состо€ние ќ”: [0,0].

–ис. 2.29. «адача парковки движущегос€ объекта
ћатематическа€ модель дл€ заданной задачи управлени€ представл€етс€ следующими уравнени€ми движени€:
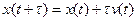
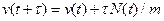 ,
,
где  Ц положение тележки на дороге, представленной одномерной осью
Ц положение тележки на дороге, представленной одномерной осью 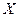 в модели объекта на рис.2.29;
в модели объекта на рис.2.29; 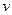 Ц скорость движени€ тележки;
Ц скорость движени€ тележки; 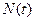 Ц сила управлени€, приложенна€ к тележке;
Ц сила управлени€, приложенна€ к тележке; 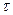 Ц шаг управлени€, m Ц масса тележки.
Ц шаг управлени€, m Ц масса тележки.
ѕрежде всего, вспомним, какие шаги должны быть сделаны при построении Ќ–:
Ј описание входных и выходных переменных и их множеств значений (“аблица 2.5а);
Ј разбиение множеств значений на подмножества значений;
Ј описание этих подмножеств с помощью нечетких множеств с заданными функци€ми принадлежности (рис.2.30);
Ј построение множества нечетких правил (“аблица 2.5 б).
»так, на вход Ќ– поступают значени€ следующих переменных:
Ј  Ц положение тележки;
Ц положение тележки;
Ј 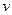 Ц скорость движени€ тележки.
Ц скорость движени€ тележки.
Ќа выходе Ц значени€ силы управлени€ 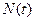 , приложенной к тележке.
, приложенной к тележке.
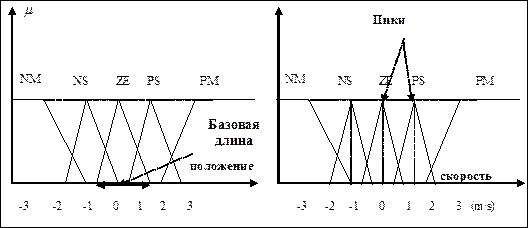
–ис. 2.30. ‘ункции принадлежности
ѕространство изменени€ переменных  ,
, 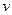 и
и 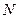 будем описывать с помощью следующих лингвистических переменных {NM, NS, ZE, PS, PM} = {Ђnegative mediumї, Ђnegative smallї, ЂZeroї, Ђpositive smallї, Ђpositive mediumї}.
будем описывать с помощью следующих лингвистических переменных {NM, NS, ZE, PS, PM} = {Ђnegative mediumї, Ђnegative smallї, ЂZeroї, Ђpositive smallї, Ђpositive mediumї}.
Ѕудем рассматривать следующие нечеткие правила:
≈—Ћ»  есть {NM,Е, PM} » v есть {NM,Е, PM}
есть {NM,Е, PM} » v есть {NM,Е, PM}
“ќ 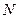 есть {NM, NS, ZE, PS, PM}.
есть {NM, NS, ZE, PS, PM}.
ѕриведенный тип правил соответствует модели нечеткого вывода ћамдани.
¬ общем виде правила в такой модели выгл€д€т следующим образом:
ѕравило l: ≈—Ћ» 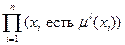 “ќ
“ќ 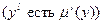 ,
,
где 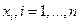 Ц входные лингвистические переменные, Ђ
Ц входные лингвистические переменные, Ђ ї операци€ нечеткой конъюнкции.
ї операци€ нечеткой конъюнкции.
¬ общем виде выходное значение в модели ћамдани (с нечеткой конъюнкцией в виде умножени€, синглетон -фаззификатором и дефаззификатором Ђсредний максимумї) вычисл€етс€ по следующей формуле:
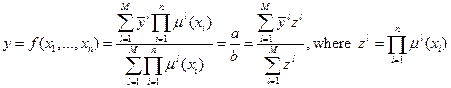 ,
,
где 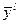 - точка максимального значени€ (центра) функции
- точка максимального значени€ (центра) функции 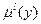 .
.
–азличные Ќ– имеют различные функции принадлежности и различные множества нечетких правил.
Ќашей задачей €вл€етс€ найти оптимальное множество нечетких правил так, чтобы Ќ– осуществл€л задачу управлени€ за минимальное врем€.
ѕервый шаг в применении √ј Ц выбор способа кодировани€ потенциальных решений.
„то такое Ђпотенциальные решени€ї дл€ нашей задачи? Ёто множество нечетких правил (Ќѕ), которое может быть представлено в виде так называемой таблицы Ђlook-up-tableї, показанной в “аблице 2.5 б.
¬ведем следующее кодирование дл€ типа функций принадлежности (лингвистических переменных) внутри “аблицы 2.5:
1 - NM, 2 - NS, 3 - ZE, 4 - PS, 5 - PM.
|
|
|
| “аблица 2.5 а ѕараметры модели | “аблица 2.5 б ћножество Ќѕ |
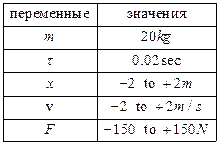
|
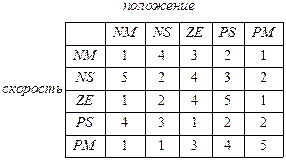
|
¬ыставив все значени€ строк таблицы в одну строку, получим строку из 25 позиций - {1432152432124514312211345}, которую легко перевести в бинарную строку, котора€ и будет служить хромосомой дл€ данной задачи оптимизации с помощью √ј. «ададим также важные параметры √ј поиска: размер попул€ции = 100; максимальное число генераций = 100; веро€тность скрещивани€ = 0.7; веро€тность мутации = 0.03.
¬ качестве оператора селекции используетс€ разновидность метода Ђtournament selectionї: две или более хромосомы выбираютс€ случайным образом и их значени€ пригодности сравниваютс€. ’ромосомы с большими значени€ми пригодности копируютс€ в следующую генерацию. ƒл€ лучшего поиска решени€, √ј процесс раздел€етс€ на две стадии: стади€ 1, называема€ Ђэволюциейї, и стади€ 2, называема€ Ђrefinement stageї. Ќа первой стадии √ј ищет приемлемые решени€ по управлению такие, что ошибка управлени€ минимальна (заданное значение). Ќа второй стадии отбираютс€ решени€ с минимальным временем, перевод€щим состо€ние ќ” из положени€  в целевое положение [0,0]. ќпишем стадию 1.
в целевое положение [0,0]. ќпишем стадию 1.
—тади€ 1.
„исло генераций равно 30. ‘ункци€ пригодности (‘ѕ) Ђнаграждаетї каждое решение в зависимости от того, как близко данное решение к заданному пределу ошибки управлени€ = 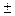 0.5 по
0.5 по  и по
и по 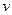 .
.
¬ведем функцию пригодности √ј дл€ оценки пригодности текущей хромосомы, представл€ющей собой множество нечетких правил, т.е. некоторый Ќ–. ƒл€ вычислени€  и
и 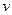 используетс€ математическа€ модель.
используетс€ математическа€ модель.
‘ункци€ пригодности дл€ стадии 1 (эволюции):
(if (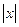 < 0.5) and (
< 0.5) and (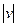 < 0.5) then fitness =
< 0.5) then fitness = 
%{  и
и 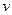 в пределах значений ошибки управлени€}
в пределах значений ошибки управлени€}
else (if (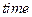 = 175) then
= 175) then
%{максимальное число шагов управлени€ задачи}
(if (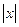 < 1.0) and (
< 1.0) and (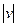 < 1.0) then fitness =
< 1.0) then fitness = 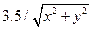 else fitness =
else fitness = 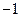 )
)
if ((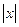 > 5.0) and (
> 5.0) and (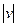 > 5.0) then fitness =
> 5.0) then fitness = 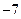 ).
).
ѕримечание: «а символом Ђ%ї идет комментарий.
ќбсудим данную функцию. ≈сли хромосома успешна по критерию качества управлени€, то она оцениваетс€ в зависимости от времени, необходимого дл€ выполнени€ задачи управлени€. ћинимальное значение ‘ѕ в этом случае равно 8 (так как 175 Ц заданный лимит шагов управлени€).
≈сли хромосома выходит за рамки Ђ175 шаговї, то она или Ђпоощр€етс€ї положительным значением ‘ѕ (если удовлетворительное качество управлени€ (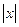 < 1.0) и (
< 1.0) и (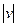 < 1.0) или Ђнаказываетс€ї отрицательным значением ‘ѕ, если плохое качество управлени€. ≈сли хромосома неуспешна по критерию качества управлени€ (
< 1.0) или Ђнаказываетс€ї отрицательным значением ‘ѕ, если плохое качество управлени€. ≈сли хромосома неуспешна по критерию качества управлени€ (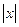 > 5.0) и (
> 5.0) и (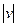 > 5.0), то она наказываетс€ большим отрицательным значением ‘ѕ.
> 5.0), то она наказываетс€ большим отрицательным значением ‘ѕ.
–исунки внизу 2.31 и 2.32 иллюстрируют структуру хромосомы и процесс вычислени€ функции пригодности.

–ис. 2.31. »ллюстраци€ процесса декодировани€ хромосомы
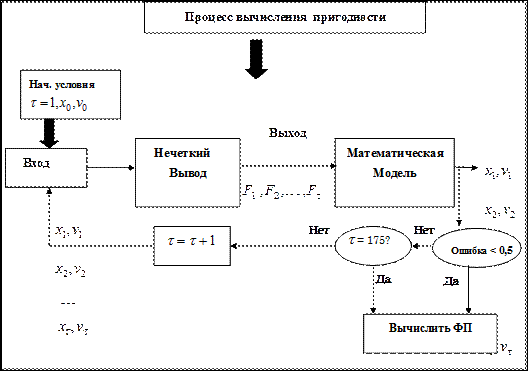
–ис. 2.32. —хема вычислени€ функции пригодности
—тади€ 2.
„исло генераций - от 31 -ой до 100-ой.
‘ункци€ пригодности дл€ стадии 2 (отбора по критерию времени):
(if (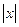 < 0.5) and (
< 0.5) and (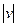 < 0.5)
< 0.5)
%{  и
и 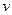 в пределах значений ошибки управлени€}
в пределах значений ошибки управлени€}
then fitness = 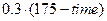
else (if (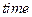 = 175) % {максимальное число шагов управлени€ задачи}
= 175) % {максимальное число шагов управлени€ задачи}
then fitness = 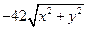 ))
))
if ((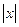 > 5.0) and (
> 5.0) and (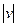 > 5.0) then fitness =
> 5.0) then fitness =  ).
).
Ќа рис. 2.33 показан результат √ј оптимизации дл€ задачи 1.
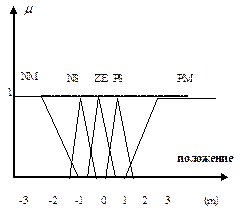 (a)
(a)
| 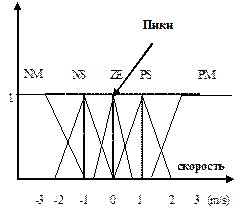 (b) (b)
|
–ис. 2.33. Ќ– с оптимально выбранным множеством Ќѕ
|
|
|
ћножество Ќѕ
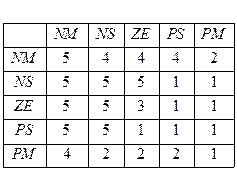 (c)
(c)
|  (d) (d)
|
–ис. 2.33. Ќ– с оптимально выбранным множеством Ќѕ
ѕримечание. Ќа рис.2.33 значени€ (а), (b) и (d) фиксированы, значени€ (c) найдены с помощью √ј.
ѕример 2. –ассмотрим следующую задачу: с помощью оптимизации, основанной на √ј, выбрать такие коэффициенты усилени€ ѕ»ƒ регул€тора 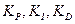 , чтобы ошибка управлени€ была минимальной (основной критерий качества управлени€).
, чтобы ошибка управлени€ была минимальной (основной критерий качества управлени€).
ќбща€ схема оптимизации коэффициентов усилени€ ѕ»ƒ регул€тора с помощью √ј показана на рис. 2.34.
ѕримечание. ¬ этом примере мы рассматриваем общие вопросы поставленной задачи без уточнени€ ќ” и цели управлени€.
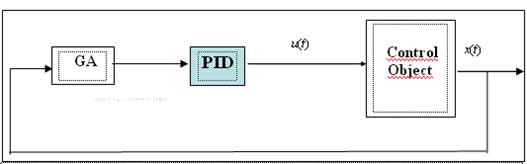
–ис. 2.34. —хема оптимизации с помощью √ј коэффициентов усилени€ ѕ»ƒ регул€тора
–ассмотрим два варианта этой задачи: 1) поиск оптимальных посто€нных коэффициентов усилени€ ѕ»ƒ регул€тора; и 2) поиск оптимальных переменных коэффициентов усилени€ ѕ»ƒ регул€тора, которые используютс€ в нечетких регул€торах;
ѕоскольку целью управлени€ (в общем виде) €вл€етс€ минимизаци€ ошибки управлени€, то в качестве функции пригодности можно выбрать, например, следующую функцию:
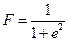 , где
, где 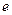 - ошибка управлени€.
- ошибка управлени€.
ќшибка управлени€ (по определению) вычисл€етс€ как
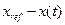 ,
,
где 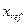 - задающий сигнал (цель управлени€), а
- задающий сигнал (цель управлени€), а 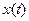 - состо€ние ќ”.
- состо€ние ќ”.
“огда, отыскива€ с помощью √ј максимум функции  , мы тем самым минимизируем ошибку управлени€
, мы тем самым минимизируем ошибку управлени€ 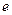 . ¬ этом случае большие значени€ функции пригодности будут соответствовать малым значени€м ошибки управлени€, а, следовательно, лучшему качеству управлени€ ѕ»ƒ регул€тора.
. ¬ этом случае большие значени€ функции пригодности будут соответствовать малым значени€м ошибки управлени€, а, следовательно, лучшему качеству управлени€ ѕ»ƒ регул€тора.
“ак как √ј работает с закодированными параметрами, обсудим способ кодировани€ дл€ нашей задачи.
¬начале рассмотрим простейший случай Ц задача оптимизации посто€нных коэффициентов усилени€ ѕ»ƒ регул€тора - 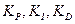 .
.
«адача 2: поиск оптимальных посто€нных коэффициентов усилени€ ѕ»ƒ регул€тора. Ѕез потери общности, предположим, что необходимо 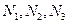 бит дл€ кодировани€ значений ѕ»ƒ параметров(
бит дл€ кодировани€ значений ѕ»ƒ параметров(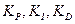 ). ¬ этом случае, размер хромосомы
). ¬ этом случае, размер хромосомы 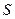 , представл€ющей значени€
, представл€ющей значени€ 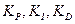 , будет
, будет 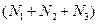 бит. ѕредставим
бит. ѕредставим 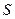 как S =
как S = 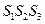 , где
, где 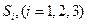 - следующие строки:
- следующие строки:
 ,
,  , и
, и  .
.
–ассмотрим, как определить число 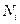 бит дл€ кодировани€ ѕ»ƒ параметров. ƒопустим, что
бит дл€ кодировани€ ѕ»ƒ параметров. ƒопустим, что
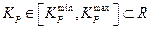 ,
, 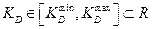 ,
, 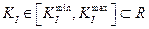 ,
,
где R есть множество всех действительных чисел.
ƒл€ каждого интервала 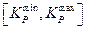 построим соответствующую решетку значений следующим образом. «ададим рассто€ние
построим соответствующую решетку значений следующим образом. «ададим рассто€ние 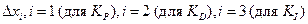 между соседними точками решетки. Ёто рассто€ние называетс€ шагом дискретизации √ј (GA discretization step). “огда общее число точек
между соседними точками решетки. Ёто рассто€ние называетс€ шагом дискретизации √ј (GA discretization step). “огда общее число точек 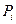 в решетке будет вычисл€тьс€ по формуле:
в решетке будет вычисл€тьс€ по формуле:
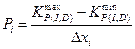 .
.
ƒл€ выбора лучшего значени€ (с точки заданной функции пригодности), например, дл€ 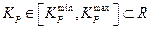 √ј исследует все точки в решетке:
√ј исследует все точки в решетке:
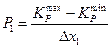
ƒлина бинарной хромосомы 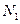 дл€ кодировани€ дес€тичного числа из
дл€ кодировани€ дес€тичного числа из 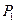 определ€етс€ по формуле:
определ€етс€ по формуле:
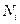 =
= 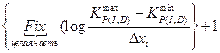 .
.
ѕримечание. ƒл€ вычислени€ значений пригодности хромосомы, бинарные значени€ 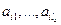 преобразуютс€ обратно в дес€тичные числа по следующей формуле:
преобразуютс€ обратно в дес€тичные числа по следующей формуле:
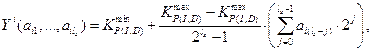
где 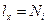 (
(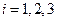 ).
).
√рафическа€ иллюстраци€ этих вычислений приведена на рис. 2.34.

–ис. 2.34. ¬ычисление значений бинарных хромосом
ѕосле того, как кодирование ѕ»ƒ параметров, функци€ пригодности и пространство поиска дл€ коэффициентов усилени€ ѕ»ƒ регул€тора определены, можно примен€ть стандартный √ј.
Ќа рисунке 2.35 показана ћатлабЦ—имулинк структура системы моделировани€ оптимальных коэффициентов усилени€ ѕ»ƒ- регул€тора.
«адача 3: поиск оптимальных переменных коэффициентов усилени€ ѕ»ƒ регул€тора дл€ нечеткого регул€тора
¬ этом случае мы имеем дело с коэффициентами усилени€ ѕ»ƒ регул€тора, завис€щими от времени. 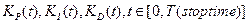 .
.
ƒл€ реализации этой задачи разработана система, названна€ SSCQ - система моделировани€ качества управлени€ (от англ. simulation system of control quality). ћатлабЦ—имулинк структура системы SSCQ показана на рис.2.36.
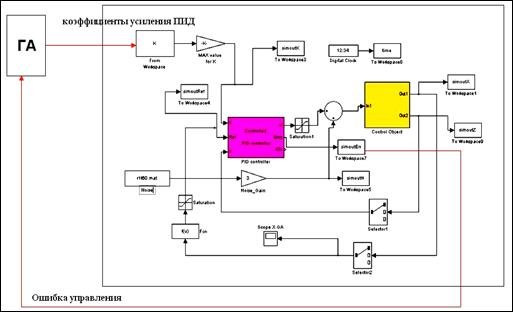
–ис. 2.35. ћатлаб/—имулинк структура системы моделировани€ оптимальных коэффициентов усилени€ ѕ»ƒ-регул€тора.

–ис. 2.36. ћатлаб/—имулинк структура системы оптимизации управлени€, основанной на √ј
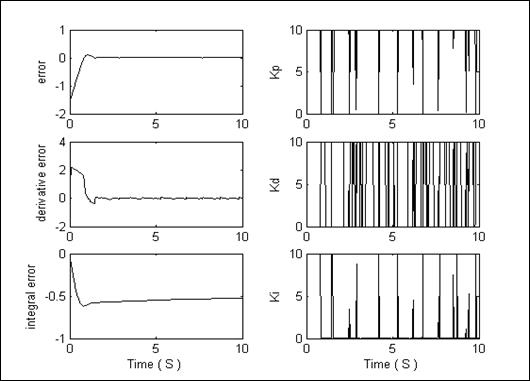
–ис. 2.37. ѕример обучающего сигнала
|
|
|
— помощью √ј находим оптимальные значени€ коэффициентов усилени€ ѕ»ƒ 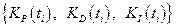 дл€ моментов времени
дл€ моментов времени 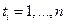 . ¬ дальнейшем эти значени€ будем называть законами управлени€. ќбъедин€€ законы управлени€ с соответствующими значени€ми ошибки управлени€ (control error), ее скорости (derivative of error) и интегральной части (integral error), получаем так называемый обучающий сигнал (ќ—) (teaching signal (TS)).
. ¬ дальнейшем эти значени€ будем называть законами управлени€. ќбъедин€€ законы управлени€ с соответствующими значени€ми ошибки управлени€ (control error), ее скорости (derivative of error) и интегральной части (integral error), получаем так называемый обучающий сигнал (ќ—) (teaching signal (TS)). ѕример ќ— показан на рис. 2.37.
ƒанный обучающий сигнал используетс€ на этапе обучени€ в нечеткой нейронной сети (ЌЌ—) (Fuzzy Neural Network (FNN)), реализующей модель нечеткого вывода —угено нулевого пор€дка.
“еори€ ЌЌ— €вл€етс€ одной из составл€ющих компонент технологии м€гких вычислений. ¬ следующем параграфе мы обсудим основные пон€ти€ ЌЌ— и алгоритмы их обучени€.
2.4. »скусственные и нечеткие нейронные сети: основные пон€ти€ и применение
¬ данной главе мы обсудим основные пон€ти€ в теории искусственных нейронных сетей (Artificial neural networks), рассмотрим обобщение на нечеткие нейронные сети и их применение.
»скусственные нейронные сети представл€ют собой математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционировани€ биологических нейронных сетей Ч сетей нервных клеток живого организма.
Ўирокое распространение »Ќ— св€зано с их следующими двум€ ключевыми характеристиками:
1) адаптивными свойствами, позвол€ющими Ђобучатьс€ на примерахї (подробнее смотри далее);
2) структура »Ќ— воплощает свойство параллелизма вычислений, что позвол€ет находить решени€ в реальном времени.
Ёти свойства »Ќ— позвол€ют использовать их дл€ решени€ следующих проблем:
Ј аппроксимаци€ функций на основе р€да данных;
Ј распознавание образов;
Ј кластеризаци€ и классификаци€ данных;
Ј обучение в области статистической обработки данных;
Ј накопление знаний через обучение на примерах;
Ј предсказание и прогноз;
Ј оптимизаци€;
Ј ассоциативна€ пам€ть;
Ј нелинейное моделирование и управление.
ѕон€тие искусственной нейронной сети (»Ќ—) возникло при изучении процессов, протекающих в коре головного мозга, и при попытке смоделировать эти процессы. —ети называютс€ Ђнейроннымиї благодар€ аналогии с нейрофизиологией, наукой о человеческом мозге и его нервной системе. »звестно, что наш мозг содержит пор€дка 1011 нейронов и имеет пор€дка 1015 св€зей между нейронами. Ёто очень большие числа. ƒл€ сравнени€, такое же количество звезд в нашей галактике Ђћлечный ѕутьї. Ќаличие такого количества взаимосв€зей определ€ет высокий уровень параллелизма в процессах обработки информации и высокую скорость реакции (нахождени€ решени€) нашего мозга. ћозг человека Ц сложна€ вычислительна€ система, состо€ща€ из нейронов различного типа (по форме и функци€м). ќдна из базовых особенностей нашего мозга €вл€етс€ Ц способность к обучению. ћоделирование этой способности €вл€етс€ также одной из основных целей в исследовани€х по разработке теории (моделей) »Ќ—.
»стори€ »Ќ— исследований восходит к работам McCuloch и Pitts (1943), Hebb (1949), Rosenblatt (1958,1961), Rochester (1956), Widrow (1960), и продолжена в работах Kohonen (1972), Hopfiled (1982), Cohen и Grossberg (1983) и др. „тобы представить различные модели »Ќ—, рассмотрим вначале общую схему работы биологического нейрона.






