Достоинством ИНС является способность к обучению, в процессе которого синаптические веса сети (или параметры сети) настраиваются с помощью того или иного адаптивного алгоритма с целью наиболее эффективного решения поставленной проблемы.
Чтобы понять или разработать обучающий процесс, прежде всего необходимо иметь некоторые знания о среде функционирования ИНС. Другими словами, нужно знать, какая информация доступна в сети.
Это так называемая парадигма обучения.
Существует три парадигмы обучения:
· супервизорное (с учителем),
· несупервизорное (без учителя),
· гибридное.
В супервизорном обучении, нейронная сеть обеспечивается правильным (корректным) выходом для заданного множества входных образов (значений).
Выбор данных для обучения сети и их обработка является самым сложным этапом решения задачи. Набор данных для обучения должен удовлетворять нескольким критериям:
· Репрезентативность — данные должны иллюстрировать истинное положение вещей в предметной области;
· Непротиворечивость — противоречивые данные в обучающей выборке приведут к плохому качеству обучения сети.
Исходные данные преобразуются к виду, в котором их можно подать на входы сети. Пара «вход-выход» называется обучающей парой или обучающим вектором.
Супервизорное обучение (обучение с учителем)
На рис. 2.48 показана схема супервизорного обучения сети.
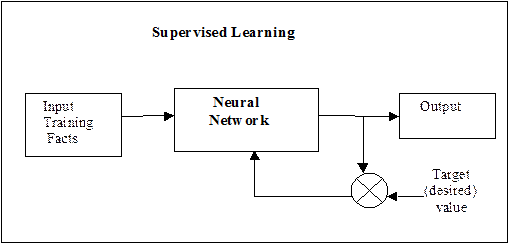
Рис. 2.48. Схема супервизорного обучения сети
При обучении с учителем набор исходных данных делят на две части — собственно обучающую выборку и тестовые (проверочные) данные; принцип разделения может быть произвольным. Обучающие данные подаются сети для обучения, а проверочные используются для проверки качества обучения сети (проверочные данные для обучения сети не применяются).
В процессе обучения используется множество обучающих пар «вход - желаемый (или целевой) выход». По обучающему входу сеть вычисляет результат, получаемый в данной структуре сети, и сравнивает его с обучающим выходом. После чего вычисляется ошибка между обучающим выходом и реальным. Просматривая обучающую выборку множество раз, сеть оптимизирует свои параметры так, чтобы ошибка была меньше заданной величины. После чего обучение заканчивается и обученную сеть можно протестировать на множестве тестовых (проверочных) данных.
Если на проверочных данных ошибка не увеличивается, то сеть действительно выполняет поставленную задачу. Если ошибка на обучающих данных продолжает уменьшаться, а ошибка на тестовых данных увеличивается, значит, сеть перестала выполнять свою задачу и просто «запоминает» обучающие данные. Это явление называется переобучением сети или оверфиттингом. В таких случаях обучение обычно прекращают.
В процессе обучения могут проявиться другие проблемы, такие как паралич или попадание сети в локальный минимум поверхности ошибок. Невозможно заранее предсказать проявление той или иной проблемы, равно как и дать однозначные рекомендации к их разрешению.
Несупервизорное обучение (обучение без учителя)
В обучении без учителя (рис.2.49) знание «обучающего (желаемого) выхода» не требуется.
Рис. 2.49. Схема несупервизорного обучения
Сеть исследует структуру входных данных и организует их в группы. В процессе обучения сеть в определенном порядке просматривает обучающую выборку. Порядок просмотра может быть последовательным, случайным и т. д. Некоторые сети, обучающиеся без учителя, например, сети Хопфилда просматривают выборку только один раз. Другие, например, сети Кохонена (также как сети, обучающиеся с учителем), просматривают выборку множество раз, при этом один полный проход по выборке называется эпохой обучения.
В отличие от супервизорного обучения, в несупервизорном обучении нет знаний о «желаемом выходе». Сеть обучается на входных данных до тех пор, пока не придет в некоторое «стабильное» состояние. В этом смысле, такая форма обучения более близка к естественному механизму в биологических нейронных сетях.
Гибридное обучение соединяет в себе черты двух приведенных выше схем обучения.
Для задач интеллектуального управления будем рассматривать супервизорное обучение сети. Рассмотрим типовой метод обучения, называемый методом обратного распространения ошибки.
Правило обучения, основанное на коррекции ошибки (Error-correction rule of learning)
Рассмотрим процесс обучения на основе правила коррекции ошибок. Это супервизорное обучение, в котором для каждого входного образа имеется желаемое выходное значение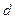 
. В процессе обучения сети реальный выход от нейронной сети 
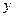не совпадает с заданным желаемым. Основным принципом обучения на основе правила коррекции ошибок является использование сигнала (значения) ошибки 
для того, чтобы настроить веса сети так, чтобы ошибка была минимальной.
Вычисление ошибки может происходить несколькими способами:
(текущая ошибка);
(среднеквадратичная ошибка);
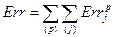(общая ошибка),
где 
- число обучающих пар; 
- число выходов нейронной сети, и 
- ошибка для -той обучающей пары.
В нейросетях существует два наиболее популярных алгоритма супервизорного обучения: обучение перцептрона (perceptron learning) и алгоритм обратного распространения ошибки (error back propagation based learning)
Обучение перцептрона (Perceptron Learning)
Рассмотрим алгоритм обучения простого перцептрона на основе правила коррекции ошибок. Напомним, что простой перцептрон (рис.2.38, 2.39) состоит из одного нейрона с настраиваемыми весами на входах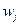 
, где 
и пороговой функцией активации.
Алгоритм обучения состоит из следующих шагов:
1) Генерируем начальные веса 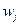(j = 0,1. 2,... n) с помощью генератора случайных (малых) чисел.
2) Поставляем на вход персептрона входной образ:
,
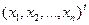где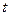 
- порядковый номер текущей итерации процесса обучения.
3) Вычисляем реальный выход персептрона:
.
4) Вычисляем ошибку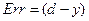 
, где 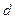- желаемый выход для входного образа .
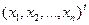5) Обновляем значения весов следующим образом:
,
где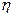 
– заданный коэффициент обучения (число между 0 и 1).
6) Повторяем шаги 2-5 до тех пор, пока ошибка не станет меньше заданного уровня толерантности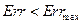 
(заданный уровень).
Теорема сходимости перцептрона, описанная и доказанная Ф. Розенблаттом, показывает, что элементарный перцептрон, обучаемый по такому алгоритму, независимо от начального состояния весовых коэффициентов и последовательности появления стимулов всегда приведет к достижению решения за конечный промежуток времени.
Алгоритм обратного распространения ошибки (error back propagation-based learning)
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона и сетей с прямым распространением сигнала (рис.2.50).
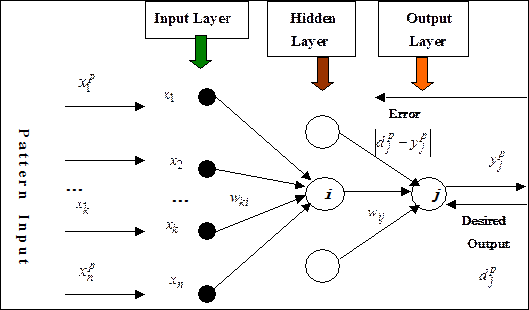
Рис. 2.50. Схематическое представление обучения на основе алгоритма обратного распространения ошибки
Важное замечание: для возможности применения этого метода функция активации нейронов должна быть дифференцируема.
Для обучения многослойного перцептрона будем использовать алгоритм обратного распространения ошибки для настраивания синаптических весов 
так, чтобы общая ошибка E была минимальной.
Для этого будем реализовывать градиентный спуск, то есть будем подправлять веса после каждого обучающего примера и, таким образом, "двигаться" в многомерном пространстве весов. Чтобы "добраться" до минимума ошибки, нам нужно "двигаться" в сторону, противоположную градиенту.
Таким образом, будем использовать следующее правило изменения весов, которое в общем виде записывается как:
на 
-ой итерации алгоритма добавлять к каждому весу его поправку
= 
, (2.18)
где 0 < η < 1 - множитель, задающий скорость "движения".
Рассмотрим многослойный перцептрон с множеством выходных вершин (рис.2.50), обозначим через - число его выходов. В качестве общей (глобальной) ошибки возьмем общую средне-квадратичную ошибку для заданного множества обучающей выборки:
, и 
,
где 
есть желаемый результат -той выходной вершины для -ой обучающей выборки, а 
- реальный результат -той выходной вершины для -ой обучающей выборки.
Вернемся к формуле (2.18).Как считать представленную в ней производную?
Две наиболее распространенные формулы приведены ниже.
Правило Дельты (Delta rule):
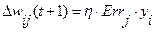
(2.19)
Обобщенное правило Дельты (Generalized delta rule):
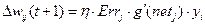(2.20)
где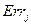 
- ошибка между желаемым и реальным значениями -той выходной вершины, 
- производная функции активации -той выходной вершины.
Обозначим функцию активации -той (любой, не только выходной) вершины как 
.
Тогда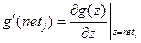 
.
Например, рассмотрим следующую логистическую функцию активации: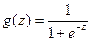 
.
Тогда
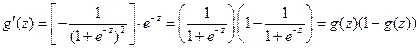(2.21)
Используя (2.21) можем написать
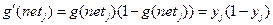(2.22)
В результате формула (2.20) может быть переписана как:
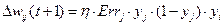(2.23)
Обсудим теперь, как вычислять ошибку ?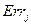
Если -тая вершина – выходная, то мы можем ее вычислить как 
, но как быть с ошибкой в скрытых слоях сети.
Рассмотрим две версии алгоритма обратного распространения ошибки.
Алгоритм обучения состоит из двух фаз: (1) фаза прямого распространения сигнала (a forward pass) и (2) фаза обратного распространения сигнала (a backward pass).
В первой фазе входные обучающие сигналы подаются в сеть и вычисляются выходные значения и выходная ошибка.
Во второй фазе процесс вычисления идет в обратную сторону – от выходной ошибки к внутренним слоям сети, в результате чего настраиваются новые значения синаптических узлов.
Алгоритм обратного распространения ошибки 1
Фаза прямого распространения сигнала:
1) Генерируем начальные веса 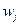(j = 0,1. 2,... n) с помощью генератора случайных (малых) чисел.
2) Случайным образом выбираем входной образ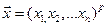 
из заданного множества обучающих пар.
3) Распространяем сигнал 
через сеть и вычисляем результат.
4) Для каждого -го выходного нейрона (слой 
) вычисляем ошибку
= .
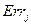Фаза обратного распространения сигнала:
1) Обновляем веса между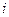 
-тыми нейронами слоя 
и -м выходным нейроном (слоя ) следующей поправкой:
,
где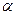 
- параметр, называемый «моментом» (momentum),
- текущая итерация процесса обучения,
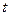- его предыдущая итерация.
2) Вычисляем ошибку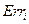 
для 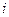-тых нейронов слоя как:
.
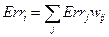3) Распространяем процесс вычисления назад по сети к 
-тым нейронам промежуточных слоев 
:
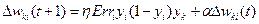и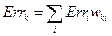 
.
4) Переходим к шагу 2 и повторяем процесс до тех пор, пока ошибка не станет меньше заданного уровня толерантности:
.
Алгоритм обратного распространения ошибки 2
1) Генерируем начальные веса 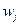(j = 0,1. 2,...n) с помощью генератора случайных (малых) чисел.
2) Случайным образом выбираем входной образ 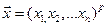из заданного множества обучающих пар.
3) Распространяем сигнал через сеть и вычисляем результат.
4) Вычисляем ошибку 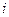-ой вершины выходного слоя (
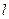= L) как:
,
где 
– производная функции активации 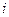-ой вершины,
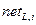– net- вход для 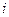-той вершины.
5) Вычисляем ошибку 
в промежуточных слоях 
, распространяя ошибку назад (с выходного слоя – к входному слою) следующим образом:
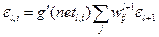для
6) Обновляем веса
for 
7) Переходим к шагу 2 и повторяем процесс до тех пор, пока ошибка не станет меньше заданного уровня толерантности 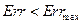или по истечению заданного числа итераций.
