Нечеткие контроллеры (Fuzzy controllers) позволяют реализовывать стратегии управления близкие человеку и представляют собой эффективную альтернативу (или дополнение) классическим системам управления.
Примечание. Будем использовать два термина для перевода «Fuzzy controllers»: нечеткие контроллеры либо нечеткие регуляторы (если речь идет о нечетком ПИД- регуляторе).
Структура нечеткого ПИД - регулятора (Fuzzy PID Controller) показана на рис. 2.18.

Рис. 2.18. Структура нечеткого ПИД – регулятора
Примечание. На рис. 2.18 используются следующие обозначения:
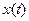 - вектор состояния объекта управления (ОУ) (a plant),
- вектор состояния объекта управления (ОУ) (a plant),  - желаемое состояние ОУ (цель управления), называемое также как «задающий сигнал» (a reference signal);
- желаемое состояние ОУ (цель управления), называемое также как «задающий сигнал» (a reference signal);  - ошибка управления (control error), вычисляемая как
- ошибка управления (control error), вычисляемая как  , где
, где  - скорость ошибки управления,
- скорость ошибки управления,  - интегральная ошибка,
- интегральная ошибка,  - сила управления, где
- сила управления, где  , где
, где  - универсумы для ошибки управления, ее производной и интегральной части, а также силы управления, соответственно.
- универсумы для ошибки управления, ее производной и интегральной части, а также силы управления, соответственно.
Отношение «вход/выход» для ПИД-регулятора выражается следующим образом:
 ,
,
где 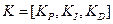 называются коэффициентами усиления ПИД-регулятора и (пропорциональный, интегральный и производный коэффициенты). Выбирая различные значения
называются коэффициентами усиления ПИД-регулятора и (пропорциональный, интегральный и производный коэффициенты). Выбирая различные значения 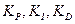 , очевидно, получаем различное поведение ОУ.
, очевидно, получаем различное поведение ОУ.
Таким образом, функционирования ОУ существенным образом зависит от выбранных параметров ПИД-регулятора. Поэтому, для разработчиков системы управления становится весьма актуальной проблема эффективного способа выбора этих параметров для того, чтобы обеспечить лучшее качество управления.
Как определить эффективный способ выбора параметров управления?
В случае классического метода управления, коэффициенты усиления ПИД-регулятора являются константами, т.е. постоянными величинами.
Чтобы усилить возможности традиционных (классических) ПИД-регуляторов, прежде всего, введем переменные коэффициенты усиления ПИД-регулятора:

Ясно, что в этом случае мы получаем больше возможностей для варьирования значениями вектора  , и для улучшения качества управления.
, и для улучшения качества управления.
Далее, будем использовать нечеткий логический подход. Нечеткое множество управления  , определенное с помощью алгоритма нечеткого вывода, в общем виде может быть представлено следующей вычислительной процедурой:
, определенное с помощью алгоритма нечеткого вывода, в общем виде может быть представлено следующей вычислительной процедурой:
 ,
,
где “ 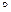 ” – композиционный оператор (смотри формулу 2.2),
” – композиционный оператор (смотри формулу 2.2),  - нечеткие множества, заданные на соответствующих универсумах, и
- нечеткие множества, заданные на соответствующих универсумах, и  есть совокупность нечетких отношений (нечетких правил), содержащихся в базе знаний нечеткого ПИД-регулятора.
есть совокупность нечетких отношений (нечетких правил), содержащихся в базе знаний нечеткого ПИД-регулятора.
Примечание. В дальнейшем будем использовать сокращенное название нечеткого ПИД-регулятора как НР.
Установив один раз нечеткие правила, с помощью нечеткого вывода мы можем реализовывать стратегии управления. Ядром нечеткого ПИД-регулятора является система нечеткого вывода Сугено.
Входные переменные для нечеткого вывода: ошибка управления, ее производная и интеграл.
Выходные переменные нечеткого вывода:  параметры.
параметры.
БЗ НР состоит из следующих нечетких правил.
Если  ,
,  - числа функций принадлежности для описания ошибки управления, ее производной и интегральной компоненты, то полная база нечетких правил содержит
- числа функций принадлежности для описания ошибки управления, ее производной и интегральной компоненты, то полная база нечетких правил содержит  нечетких правил.
нечетких правил.
Полная база выглядит следующим образом:
ЕСЛИ  И
И  И
И  есть
есть 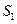 , ТО
, ТО 

ЕСЛИ  И
И  И
И  есть
есть  , ТО
, ТО 

ЕСЛИ  И
И  И
И  есть
есть 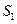 , ТО
, ТО 

ЕСЛИ  И
И  И
И  есть
есть 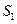 , ТО
, ТО 

ЕСЛИ  И
И  И
И  есть
есть  ТО
ТО  ,
,
где  , и
, и  – функции принадлежности для описания значений
– функции принадлежности для описания значений 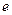 ,
,  , и
, и  , соответственно.
, соответственно.  ,
, 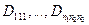 и
и  - реальные числа, удовлетворяющие условию:
- реальные числа, удовлетворяющие условию:
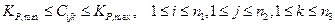
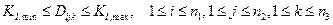
 .
.
Согласно нечеткой модели Сугено (нулевого порядка), выходное значение вычисляется следующим образом:
 ,
,  ,
,  ,
,
где  .
.
Примечание. В НР регуляторах могут использоваться более простые правила в случае, если вместо ПИД управления использовать П-управление (только  параметр,
параметр,  ), или ПД (
), или ПД ( ), или ПИ (
), или ПИ ( ) управление.
) управление.
2.2.7 Пример применения нечеткой логики: управление автомобилем на основе нечеткой логики
Вернемся к нашему примеру вождения автомобиля. Возьмем ситуацию управления автомобилем, где автомобиль движется по прямой полосе дороги, и водитель следит за автомобилем перед ним. Оценивая расстояние между автомобилями и скорость движения своей машины (информация от сенсоров), человек-водитель реализует различные стратегии управления автомобилем. Например, как показано в Таблице 2.1.
Таблица 2.1
Стратегии управления автомобилем
| Правило 1. ЕСЛИ расстояние между машинами короткое и машина едет с медленной скоростью, ТО не меняй скорость движения (ускорение нулевое). (Rule 1: IF distance between cars is short AND speed is slow, THEN hold the gas pedal steady (maintain the speed)). |
| Правило 2. ЕСЛИ расстояние между машинами маленькое и машина едет с большой скоростью, ТО тормози (ускорение отрицательное). (Rule 2: IF distance between cars is short AND speed is fast, THEN step on the brake (reduce the speed)). |
| Правило 3. ЕСЛИ расстояние между машинами большое и машина едет медленно, ТО жми на педаль газа (ускорение положительное). (Rule 3: IF distance between cars is long AND speed is slow, THEN step on the gas pedal (increase the speed)). |
| Правило 4. ЕСЛИ расстояние между машинами большое и машина едет с большой скоростью, ТО не меняй скорость движения (ускорение нулевое). (Rule 4: IF distance between cars is long AND speed is fast, THEN hold the gas pedal steady (maintain the speed)). |
Для формализации вышеприведенных правил введем следующие лингвистические переменные: «расстояние», «скорость» и «ускорение» (“distance”, “speed”, and “acceleration). Опишем значения малое» («short»), «большое» («long»), «медленно» («slow»), «тормози» («step on brake») и так далее соответствующими нечеткими множествами, как показано на рис. 2.19.
Примечание. Функции принадлежности должны быть определены в соответствии с рассматриваемой ситуацией. Так, например, скорость 70 км/час может быть большой на улице города и маленькой на скоростной трассе.
Обозначим через  - «расстояние», через
- «расстояние», через 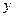 - «скорость» и
- «скорость» и  - «ускорение». Соответствующие универсумы определим следующим образом:
- «ускорение». Соответствующие универсумы определим следующим образом:
 [m]
[m]
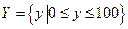 [km/h]
[km/h]

 Рис. 2.19. Функции принадлежности для введенных лингвистических переменных
Рис. 2.19. Функции принадлежности для введенных лингвистических переменных
Обозначим следующими символами введенные нечеткие множества:
 : «малое»
(“short) : «малое»
(“short)
|  : «медленно» (“slow”) : «медленно» (“slow”)
|  : «пост. скорость» (“maintain”) : «пост. скорость» (“maintain”)
|
 :«большое»
(“long”) :«большое»
(“long”)
|  : «быстро»
(“fast”) : «быстро»
(“fast”)
|  :«тормозить»
(“reduce”) :«тормозить»
(“reduce”)
|
 :«увеличить скорость» (“increase”) :«увеличить скорость» (“increase”)
| ||
| (расстояние) | (скорость) | (ускорение) |
Тогда правила из Таблицы 2.1 могут быть формализованы в виде следующих нечетких правил:
Правило 1: ЕСЛИ 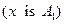 И
И  ТО
ТО 
Правило 2: ЕСЛИ 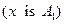 И
И  ТО
ТО 
Правило 3: ЕСЛИ  И
И  ТО
ТО 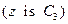
Правило 4: ЕСЛИ  И
И  ТО
ТО  .
.
Эти правила могут быть представлены таблицей, называемой таблицей «look-up table», в следующем виде:

После того, как мы формализовали правила принятия решений в виде нечетких правил, мы можем осуществлять нечеткий вывод.
В соответствии с правилами используем модель нечеткого вывода Мамдани.
На рис. 2.20 показан процесс нечеткого вывода для входных значений расстояния = 18 м и скорости = 48 км/час.
Выходное нечеткое множество может быть описано словами как «сбавить немного скорость» («reduce speed a little»). Выходное четкое значение вычисляется с помощью дефаззификатора «по центру тяжести» и обозначается на рисунке символом “ 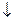 ”.
”.


Рис. 2.20. Процесс нечеткого вывода для задачи управления автомобилем






