Арифметикалық орташа шаманы есептеу кезінде жұмыс көлемін және есептеу жолдарын жеңілдету үшін төмендегідей математикалық қасиеттер қолданылады:
1. Орташа шамамен (
) жиілік қосындасын (
f) көбейтіндісі ( f) әрқашанда өзгермелі белгі мен (х) жиіліктің (f) көбейтіндісінің қосындысына ( хf) тең болады:
f = хf
2. Егер белгінің барлық жиіліктерін (f) тұрақты бір санға (А) көбейтсек немесе бөлсек, онда орташа шама өзгермейді: 
= 
= 
=
3. Егер әр қатардағы белгіге (х) тұрақты бір (А) санды қоссақ, немесе алсақ, онда орташа шама сол тұрақты санның мөлшеріне көбейеді не азаяды:
= 
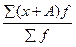A; бұдан = 
4. Егер әр қатардағы белгіні (х) тұрақты бір санға көбейтсек, немесе бөлсек, онlа жаңа белгілермен есептелген орташа шама сонша рет көбейеді не азаяды: 
= 
; бұдан = 
= 
; бұдан = 
5. Белгілердің орташа шамадан айырмалардан қосындысы әрқашанда нөлге тең болады:
(x - ) = 0 немесе (x - )f = 0 [kgl]
Арифметиалық және гармоникалық (үйлесімдік) орташа шамалар жалпы жиынтықтықтың өздеріне тән өзгермелі белгілер бойынша есептелінген қорытындылаушы көрсеткіштер. Статистикада осы өзгермелі белгілердің бөлінуін қосымша мінездеу үшін қолданатын орташа сандық шаманы құрылымдық орта деп атайды. Оған жататын – мода және медиана
Статистикалық қатарлардың ішінде ең жиі кездесетін белгінің үлкен шамасын, яғни өзгермелі сандық қатарда жиіліктің үлкен мәні жатқан белгіні мода деп атайды.Статистикада модалық орта шама зерттеп отырған белгілеріміздің мәні мен мақсатына және жиі кездесетін жиіліктің үлкен көрсеткішін қолдануымызға байланысты.
Мысалы: Кәсіпорындағы жұмысшылардың орташа айлық еңбекақысын, рынокта сатылған тауардың орта бағасын немесе халықтың көп тұтынатын аяқ киімдердің өлшемін анықтау үшін модалық орташаны қолданамыз.
Егер статистикалық қатарлардың белгісі бүтін сан шамасымен берілетін болса, онда сол берілген белгінің ең үлкен жиілік мәні жатқан қатар, мода болып саналады. Мұндай жағдайда моданы оп-оңай анықтауға болады.
| Айлық еңбекақы мөлшері, х | Жұмысшылар саны, f | Жалпы айлық еңбекақы, хf |
| Барлығы |
Ең жиі кездесетін еңбекақы мөлшері 29000 теңге модалдық көрсеткіш болып саналады.
Егер статистикалық қатарлар белгілерінің ең үлкен жиілік мәні екі сандық көрсеткішпен берілсе, онда модалдық белгі екеу болады. Ал, жиілік мәндері бірдей бірнеше белгі берілетін болса, онда модалдық көрсеткіш болмайды.
Кейде қатар белгілері бүтін сан емес, деңгей аралықты шамамен берілуі мүмкін. Мұндай жағдайда модалдық орташа шаманы анықтау үшін статистикалық формуланы қолданамыз.
Статистикада мода – М 
- әрпімен белгіленеді және деңгей аралықта қатар берілген болса, келесі формула арқылы есептеледі:
М = x 
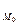+ d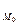 
;
мұндағы: x 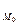- модалық қатардың деңгей аралығының кіші мәні;
d 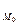- модалық қатардың деңгей аралығының айырмасы;
- модалық қатардың жиілігі;
- модалық қатардың алдыңғы қатар жиілігі;
- модалық қатардан кейінгі қатар жиілігі;
| Айлық еңбекақы мөлшері бойынша топқа бөлу, тг (х) | Жұмысшылар саны, адам (f) | Жиіліктің жиналған қосындысы (s) |
| 20000-22000 | ||
| 22000-24000 | ||
| 24000-26000 | ||
| 26000-28000 | ||
| 28000-30000 | ||
| Барлығы | - |
Берілген мәліметтер бойынша мода 2400-2600 теңгелік қатарда жатыр, себебі бұл қатарға ең үлкен жиіліктің мәні келіп тұр
М =24000+2000 
= 24000+2000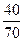 
=25140,20 тг
яғни 100 жұмысшының модалық орташа еңбекақы мөлшері 2514,20 теңгеден болды, бұл – жиілігі ең үлкен қатарда жатыр деген.
Медиана деп статистикалық өзгермелі қатардың ортасында жатқан белгіні атайды. Медиана – статистикалық қатарды теңдей етіп екіге бөледі және оның екі жағында (жоғары, төмен) жатқан белгілердің сандық бірліктері бірдей болады.
Статистикада медиана М 
- әрпімен белгіленеді және оны есептеу берілген сандық белгілердің мәніне байланысты.
Егер статистикалық қатарлардың белгісі бүтін сан шамасында берілетін болса, медиананы анықтау үшін келесі формуланы қолдануға болады:
М = 
мұндағы: п - статистикалық қатарлар саны
Мысалы: Бір цехта жұмыс істейтін 5 жұмысшының әрқайсысы 30,31,32,34 және 35 дана тетіктен өңдеп шығарған десек, медиана 32-ге тең болады, яғни медиана үшінші қатарда жатады:
М = = 
= 3 қатар
Біздің мысал бойынша медиана үшінші және төртінші белгілердің қосындысының жартысына
= 33 данаға сәйкес келеді
Ал, деңгей аралықты қатардан медиананы есептеу үшін келесі формуланы қолдануға болады.
М = x 
+ d 
= 
;
x -медианалық қатардың деңгей аралығының кіші мәні
d - медианалық қатардың деңгей аралығының айырмасы
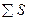- медианалық жиіліктің қосындысы
- медианалық қатардың алдыңғы қатардағы жинақталған жиілік қосындысы
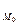М = x + d ;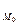
x 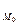- модалық қатардың деңгей аралығының кіші мәні -50 мин
d 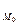- модалық қатардың деңгей аралығының айырмасы – 10 мин
- модалық қатардың жиілігі – 17 адам
- модалық қатардың алдыңғы қатар жиілігі – 10 адам
- модалық қатардан кейінгі қатар жиілігі – 1адам
М = x + d ; М = x + d 
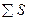- мединалық жиіліктің қосындысы – 35
- медианалық қатардың алдыңғы қатардағы жинақталған жиілік қосындысы
Қоғамдағы болатын әр түрлі құбылыстар мен процестердің өзгермелігін вариациясын зерттеу үшін статистика вариация көрсеткіштерін қолданады. Белгілердің шамасы әр түрлі факторлардың әсер етуіне сәйкес олардың арасында өзгеріс туады, яғни үлкенді-кішілі ауытқулар болады.
Егер қатар белгілердің жеке мәндерінің бір-бірінен азайған өзгерістері болған жағдайда, орташа шама сол жиынтық үшін дұрыс деп саналады.
Егер қатар белгілердің жеке мәндерінің бір-бірінен ауытқуы көп болған жағдайда орташа шама сол жиынтық үшін дұрыс немесе бұрыс екенін көрсетеді.
Белгілердің өзгермелігін міндеттеу үшін нақты және қатысты көрсеткіштер системалары қолданады.
3. Өзгерменің көрсеткіштері туралы түсінік және оның көрсеткіштері, өзгерменің көрсеткіштерін есептеу тәсілдері
1. Өзгерменің немесе вариацияның нақты көрсеткіштері
1. Өзгерменің өрісі R деп белгілесек, онда
R = x 
– x 
мұндағы: x - сандық қатар белгілерінің үлкен мәні
x -сандық қатар белгілерінің кіші мәні.
2. Орташа сызықтық ауытқу 
-әрпімен белгіленеді:
= 
жай түрі
= 
өлшемдес немесе салмақталған түрі
мұндағы: х - белгілердің жеке сандық мәндері;
- белгілердің орташа шамасы;
п - белгілердің саны;
f - жиілік көрсеткіштерінің жеке мәндері
3. Дисперсия 
= 
жай түрі
= 
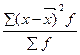салмақталған түрі
Статистикадада дисперсия (шашыранды) көптеген әлеуметтік-экономикалық көрсеткіштерді талдау үшін қолданылады.
4. Орташа квадраттық ауытқу 
- әрпімен белгілейді
= = 
жай түрі
= = 
салмақталған түрі
2. Өзгерменің қатысты көрсеткіштері:
1. Осцилляция коэффиценті:
= 
;
2. Өзгерменің сызықтық коэффиценті:
= 
3. Өзгерменің коэффиценті:
V = 
Дисперсия және орташа квадраттық ауытқу белгілердің өзгермелігін мінездеу үшін жеткіліксіз, сондықтан қатысты немесе салыстырмалы көрсеткіштер қолданылады.
