Розділ ІУ. Додавання і віднімання багатоцифрових чисел.

 

Метою розділу є формування в учнів навичок письмового додавання та віднімання багатоцифрових чисел. Слід зазначити, що з письмовим прийомами додавання та віднімання учні ознайомились у 3-му класі, на початку навчального року в 4-му класі алгоритми письмових прийомів були актуалізовані, водночас розглядалось письмове додавання у випадку трьох доданків. Таким чином, тривалий час було відведено для формування в учнів обчислювальних навичок, і до даного етапу можна очікувати, що учні володіють прийомами письмового додавання та віднімання трицифрових чисел. Таким чином, існує можливість перенесення відомого учням способу міркування на випадки письмового додавання і віднімання багатоцифрових чисел. За допомогою навчальних завдань учні переконуються, що письмове додавання та віднімання багатоцифрових чисел відбувається так само, як і трицифрових. Слід зазначити, що вправи в усних обчисленнях не припиняються, і учні вдосконалюють навички усних обчислень з круглими багатоцифровими числами.

У межах цього розділу продовжуємо розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків, які були введені в 3-му класі; також триває робота над вивченими типовими задачами: на знаходження четвертого пропорційного (спосіб відношень); на знаходження суми та різницеве порівняння двох часток та оберненими до них тощо.

Особливу увагу приділяємо ознайомленню із групою взаємопов’язаних величин, які описують процес руху тіла: швидкість, час руху та подоланий шлях та розв’язуванню, спочатку простих, а потім й складених задач із цими величинами.

Триває робота над рівняннями, нерівностями зі змінною, учні знаходять значення виразів зі змінною; розв’язують задачі геометричного змісту.

Завершується тема арифметичними діями додавання і віднімання іменованих чисел, які вимагають застосування письмового прийому.

 

Урок №48 (100 – 101)

Мета: узагальнити і систематизувати навчальний досвід учнів стосовно арифметичних дій додавання та віднімання

Дидактичні задачі. Вдосконалювати навички усних обчислень (№1). Актуалізувати навчальний досвід учнів відносно додавання та віднімання (форзаци); правил віднімання суми від числа, додавання числа до суми, віднімання суми від числа, віднімання числа від суми (№2); застосування законів додавання, правил додавання й віднімання для раціоналізації обчислень. Актуалізувати уміння порівнювати багатоцифрові числа та визначати різницеве відношення між числами; вдосконалювати навички віднімання чисел на підставі нумерації; вдосконалювати вміння порівнювати математичні вирази, навички додавання і віднімання багатоцифрових чисел на підставі нумерації. Актуалізувати розуміння залежності значення суми від зміни одного з доданків, значення різниці від зміни зменшуваного або від’ємника. Формувати уміння розв’язувати складені задачі, що містять збільшення або зменшення числа на кілька одиниці, в тому числі сформульовані у непрямій формі. Вдосконалювати навички ділення трицифрового числа на двоцифрове. Розвивати вміння розв’язувати рівняння, в яких один з компонентів або права частина подана числовим виразом (№8). Вдосконалювати навички усного додавання і віднімання круглих чисел способом укрупнення розрядних одиниць; навички письмового додавання та віднімання трицифрових чисел.

Розвивальна задача: розвивати логічне мислення учнів (№9).

 

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Знайомство із чотирицифровими, п’ятицифровими, шестицифровими числами дозволяє нам піднятися на наступну сходинку – розглянути дії із ними. Розкажіть, коли у людини є необхідність додавати і віднімати багатоцифрові числа. Здогадайтесь, чи відрізнятимуться ці дії від дій із трицифровими числами. Чим саме? Сьогодні у нас буде нагода перевірити, які знання і вміння з 3-го класу стануть вам корисними.

ІІ. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО

1. Усна лічба.

Завдання №1 виконується учнями самостійно.

2. Усне опитування (використовуються форзаци).

Див. урок №2.

3. Узагальнення і застосування законів та правил додавання; правил віднімання для раціоналізації обчислень.

Завдання №2 виконується колективно.

Перша рівність: щоб відняти суму від числа, достатньо від цього числа відняти спочатку один доданок, а потім від одержаного результату відняти інший доданок – правило віднімання суми від числа.

Друга рівність: щоб додати число до суми, достатньо це число додати до одного з доданків, а потім до одержаного результату додати інший. Це формулювання сполучного закону додавання.

Третя рівність – аналогічно до першої.

Четверта рівність: щоб відняти число від суми, достатньо це число відняти від одного з доданків, а потім до одержаного результату додати інший – правило віднімання числа від суми.

Пропонуємо учням зіставити першу та четверту рівності: відмінне - при відніманні суми від числа ми віднімаємо обидва доданки, а при відніманні числа від суми ми віднімаємо це число з одного з доданків. Зіставляємо сполучний закон додавання та правило віднімання числа від суми: спільне те, що це число ми або додаємо або віднімаємо з одного з доданків суми, а потім до одержаного результату додаємо інший доданок.

Завдання №3 виконується з коментарем.

Зазначимо, що для знаходження значень перших двох виразів використовується переставний закон додавання: числа можна додавати у будь-якому порядку.

Завдання №1 із робочого зошита виконується учнями самостійно.

4. Закріплення знання правила різницевого порівняння чисел та уміння його застосовувати; вдосконалення обчислювальної навички віднімання на підставі розрядного складу багатоцифрових чисел.

Завдання №4 виконується з коментарем.

Пригадуємо правило різницевого порівняння: щоб дізнатися, на скільки одне число більше або менше за інше, треба від більшого числа відняти менше.

5. Формування навичок усного додавання і віднімання круглих багатоцифрових чисел із застосуванням прийому укрупнення розрядних одиниць.

Завдання № 2 із робочого зошита виконується учнями самостійно.

Пригадуємо суть прийому укрупнення розрядних одиниць. Звертаємо увагу на те, що маємо замінювати обидва числа однаковими більшими розрядними одиницями – це дає можливість виконувати обчислення в межах 100.

6. Закріплення розуміння залежності значення суми від зміни одного з доданків; значення різниці від зміни зменшуваного; від’ємника.

Завдання №5 виконується колективно.

Учні обчислення не виконують. Коментар будується на підставі правил: 1) якщо один доданок збільшити (зменшити) на кілька одиниць, а інший лишити сталим, то значення суми так само збільшиться (зменшиться) на стільки ж одиниць; 2) якщо зменшуване збільшити (зменшити) на кілька одиниць, а від’ємник лишити сталим, то значення різниці, так само, збільшиться (зменшиться) на стільки ж одиниць; якщо від’ємник збільшити (зменшити) на кілька одиниць, а зменшуване лишити сталим, то значення різниці, навпаки, зменшиться (збільшиться) на стільки само одиниць.

Завдання №3 із робочого зошита виконується з коментарем.

Порівнюючи перші два вирази учні помічають, що збільшився другий доданок, тому й значення суми, так само, збільшиться. У другому рядку: зменшилося зменшуване, тому значення різниці, так само, зменшиться. У третьому – збільшився від’ємник, тому значення різниці, навпаки, зменшилось. У четвертому: збільшився перший доданок, тому значення різниці, так само, збільшиться.

7. Вдосконалюємо обчислювальні навички письмового додавання та віднімання трицифрових чисел.

Завдання №4 із робочого зошита виконується з коментарем.

Звертаємо увагу: 1) підписуємо числа стовпчиком – одиниці під одиницями, десятки під десятками, сотні під сотнями; 2) додавання (віднімання) починаємо з розряду одиниць; 3) пам’ятаємо, що 10 одиницю нижчого розряду становить 1 одиницю вищого або 10 одиниць нижчого розряду становлять 1 одиницю вищого.

8. Вдосконалення уміння розв’язувати складені задачі.

Завдання №6 виконується колективно.

Зіставляючи задачі 2 і 1 учні помічають, що задачу 2 можна звести до задачі 1, якщо переформулювати різницеве відношення кількості телефонів, що відремонтував майстер першого та другого дня. В задачі 2 різницеве відношення між кількостями І-го та ІІ-го днів сформульовано непрямо. Задачі 1 і 2 матимуть одне й те саме розв’язання. У задачі 3, порівняно із задачею 2 вже два різницевих відношення сформульовані непрямо. Учні змінюють задачу: якщо другого дня відремонтовано 12 телефонів, а це на 7 більше, ніж першого, то першого дня відремонтовано на 7 менше, ніж другого; якщо другого дня відремонтовано 12 телефонів, а це на 3 більше, ніж третього, то третього відремонтовано на 3 менше, ніж другого. Задачу 3 учні розв’язують самостійно.

 

9. Вдосконалення навичок письмового ділення та множення у межах 1000.

Завдання №7 виконується учнями самостійно.

10. Вдосконалення уміння розв’язувати рівняння.

Завдання №8 виконується учнями самостійно.

Два рівняння, позначені магістерською шляпою виконуються учнями на дошці.

11. Розвиток логічного мислення учнів.

1) Якщо огорожа розташована вздовж дороги, то кількість проміжків між стовпами на 1 менше, ніж стовпів: 5 – 1 = 4 (проміжки). За умовою задачі відстань між сусідніми стовпами 2 м, маємо: 2 * 4 = 8 (м) довжина огорожі.

2) Якщо огорожа розташована уздовж замкненої лінії, то кількість проміжків між стовпами дорівнює кількості стовпів – 5 проміжків. 2 * 5 = 10 (м) довжина огорожі.

 

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №7 – виконати ділення на двоцифрове число, використовуючи письмовий прийом; перевірити правильність результату множенням.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Що спільне у прийомах обчислення, якими користувалися на уроці із тими, які використовували в 3-му класі? Що на уроці було не складним? Які завдання викликали труднощі? Яких успіхів вдалося сьогодні досягти

 

Урок №49 (с. 102 – 103)

Мета: формувати навички письмового додавання та віднімання багатоцифрових чисел

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати способи міркування при усному додаванні та відніманні: додавання (віднімання) способом укрупнення розрядних одиниць, додавання (віднімання) частинами на підставі правила додавання (віднімання) сумі до (від) числа; додавання (віднімання) на підставі правила додавання (віднімання) числа до (від) суми; порозрядне додавання (віднімання); додавання (віднімання) способом округлення, та вміння їх застосовувати при додаванні та відніманні круглих багатоцифрових чисел у випадках, які зводяться до додавання та віднімання в межах 100. Актуалізувати письмовий прийом додавання та віднімання трицифрових чисел. Створити проблемну ситуацію, за якої виявляється неможливим застосувати усні прийоми для обчислення сум та різниць Розв’язувати проблемну ситуацію, в наслідок чого здійснити ознайомлення із письмовим прийомом додавання та віднімання багатоцифрових чисел. Формувати уміння виконувати письмове додавання та віднімання багатоцифрових чисел. Формувати уміння розв’язувати складені задачі, що містять збільшення або зменшення числа на кілька одиниць, сформульовані у непрямій формі. Вдосконалювати уміння розв’язувати задачі на час; задачі на роботу з даними. Формувати уміння обчислювати значення виразів зручним способом.

 

Розвивальна задача: розвивати логічного мислення учнів (с. 127 №1).

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Пригадайте, які знання допомогли вам у 3-му класі опанувати письмові прийоми додавання і віднімання трицифрових чисел. Здогадайтесь, які з них можуть бути корисними під час виконання дій із чотирицифровими, п’ятицифровими, шестицифровими числами. Сьогодні на уроці ми зможемо перевірити вашу здогадку. Помітьте, що в матеріалі уроку для вас буде новим, а що – відомим.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 із робочого зошита виконується учнями самостійно.

Завдання №7.

2. Усне опитування.

Див. усне опитування до уроку №4. Додатково: У чому суть прийому укрупнення розрядних одиниць? Чи можна числа замінювати різними більшим розрядними одиницями: наприклад, одне число тисячами, а інше – сотнями? Які прийоми усного додавання (віднімання) ви знаєте? На якому правилі ґрунтується додавання (віднімання) частинами? Чому цей прийом називається обчисленням частинами? Які ще прийоми додавання (віднімання) вам відомі?

3. Актуалізація відомих учням усних прийомів обчислення.

Завдання №1 виконується колективно.

використано прийом укрупнення розрядних одиниць: замінюємо обидва доданки однаковими більшими розрядними одиницями; додаємо числа розрядних одиниць, результат подаємо у одиницях.

- прийом додавання частинами, на підставі правила додавання суми до числа: другий доданок замінюємо сумою розрядних доданків; додаємо суму до числа, для цього до нього додаємо перший доданок, а до одержаного результату – додаємо другий доданок.

Звертаємо увагу учнів на те, що можна було б виконати обчислення частинами, замінивши другий доданок сумою зручних доданків.

- прийом на підставі правила додавання числа до суми: перший доданок подаємо у вигляді суми розрядних доданків; додаємо число до суми, для цього це число додаємо до першого доданка і до одержаного результату додаємо інший доданок.

Можна застосувати ще й інший спосіб міркування на підставі даного правила, замінивши перший доданок сумою зручних доданків.

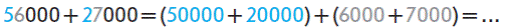- прийом порозрядного додавання: замінюємо перший доданок сумою розрядних доданків; замінюю другий доданок сумою розрядних доданків; додаю десятки тисяч; додаю одиниці тисяч; додаю одержані результати.

- прийом округлення: замінюємо другий доданок близьким розрядним числом; під час додавання помічаємо, на скільки більше будемо додавати, віднімаємо стільки ж одиниць; виконуємо обчислення.

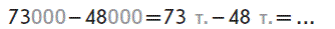- прийом укрупнення розрядних одиниць. Міркування аналогічні до відповідного способу міркування при додаванні.

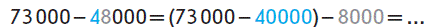- прийом віднімання частинами: замінюємо від’ємник сумою розрядних доданків; відмітаємо суму від числа, для цього від числа віднімаємо спочатку один доданок, а потім, від одержаного результату віднімаємо інший доданок.

Можна виконати віднімання частинами іншим способом – замінивши від’ємник сумою зручних доданків.

- прийом на підставі правила віднімання числа від суми: зменшуване подаємо у вигляді суми розрядних доданків; від суми віднімаємо число, для цього це число віднімаємо від одного з доданків суми, а потім до одержаного результату додаємо інший доданок суми.

Можна зменшуване замінити сумою зручних доданків.

- прийом порозрядного віднімання: зменшуване подаємо у вигляді суми зручних доданків, де перший доданок десятки тисяч, але на один десяток тисяч менше, а другий доданок – одиниці тисяч; від’ємник подаємо у вигляді суми розрядних доданків; віднімаємо десятки тисяч; віднімаємо одиниці тисяч; додаємо одержані результати.

- прийом округлення: від’ємник замінюємо близьким розрядним числом; відніматимемо це розрядне число, визначаємо на скільки більше відніматимемо, тому додаємо стільки ж одиниць; обчислюємо.

4. Актуалізація письмового прийому додавання та віднімання трицифрових чисел.

Завдання №2 із робочого зошита виконується з коментарем.

 

ІІІ. ФОРМУВАННЯ НОВИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Мотивація введення письмового прийому додавання та віднімання багатоцифрових чисел.

Завдання № 2 виконується колективно.

Значення другого виразу у стовпчику можна знайти шляхом порозрядного обчислення, але це дещо складніше, ніж для першого виразу стовпчика. У складніших випадках обчислення використовують письмовий прийом.

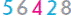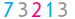Пропонуємо учням зіставити суму + з другою сумою першого стовпчика, і з’ясувати, чи можна в цьому випадку застосувати прийом порозрядного додавання? Теоретично можна, але це дуже складно! В цьому випадку вже потрібно використовувати письмовий прийом. Пригадуємо, як доцільно міркувати при письмовому додаванні. Аналогічно зіставляємо різницю - з другою різницею у другому стовпчику.

2. Перенесення письмового прийому додавання та віднімання на випадки обчислень з багатоцифровими числами.

Пропонуємо учням завдання:

НЗ Ч.2 с.12

Висновок: чотирицифрові, п’ятицифрові, шестицифрові числа додають (віднімають) так само як і трицифрові. Першим кроком підписуємо числа стовпчиком розряд під розрядом; додавання (віднімання) починаємо з розряду одиниць; при додаванні (відніманні) пам’ятаємо, що 10 одиниць нижчого розряду становлять одну одиницю вищого (що 10 одиниць нижчого розряду становлять 1 одиницю вищого).

3. Первинне закріплення.

Завдання №3 виконується з коментарем.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування навичок письмового додавання і віднімання багатоцифрових чисел.

Завдання№4 виконується з коментарем.

Завдання №3 із робочого зошита виконується учнями самостійно.

2. Формування уміння застосовувати закони і правила додавання і віднімання для раціоналізації обчислень.

Завдання №4 із робочого зошита виконується учнями самостійно.

3. Вдосконалення вміння розв’язувати складені задачі.

Учні разом із вчителем змінюють задачу: , то від Умані до Києва на 60 км менше, ніж від Одеси до Умані. Далі учні самостійно розв’язують задачу.

 

4. Розвиток логічного мислення учнів.

За наявності резерву часу пропонуємо учням задачу:

В класі 25 учнів. З них 6 учнів або не вміють грати в шашки, або в шахи. 18 учнів вміють грати в шашки, 20 – в шахи. Скільки учнів класу грають і в шашки і в шахи?

Розв’язання. Відомо, що 18 учнів грають в шашки, тому 25 – 18 = 7 учнів не вміють грати в шашки. Якщо ми із 7 – 6 = 1 учнів не вміють грати в шашки, але можуть вміти грати в шахи. Так як 20 учнів вміли грати в шахи, то 20 – 1= 19 учнів могли грати і в шахи і в шашки.

Відповідь: 19 учнів

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №4 – виконати додавання і віднімання, використовуючи письмовий прийом; перевірити правильність результату. Завдання №6 – накреслити в зошиті таблицю і вписати дату прибуття потягу, для цього розв’язати задачу на знаходження часу закінчення події.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Чи справдилася ваша здогадка з початку уроку? Чим подібні письмові прийоми додавання і віднімання трицифрових чисел і багатоцифрових? Що було на уроці зовсім новим? Що було для вас відомим? Чи відчували ви складнощі? Які саме? Що було в роботі успішним?

 

 

Урок №50(с. 104 – 105)

Мета: формувати навички письмового додавання та віднімання багатоцифрових чисел

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати прийом додавання і віднімання багатоцифрових чисел, з’ясувати доцільність переставляння доданків у випадку додавання більшого числа до меншого. Актуалізувати прийом письмового додавання трицифрових чисел у випадку трьох доданків; перенести спосіб міркування на випадки додавання багатоцифрових чисел. Формувати навички письмового додавання трьох доданків у межах багатоцифрових чисел, в тому числі із застосуванням переставного закону додавання; навички письмового віднімання багатоцифрових чисел, перевірки правильності виконання обчислення. Формувати навички письмового додавання багатоцифрових чисел; уміння досліджувати залежності значення суми від зміни обох доданків. Формувати уміння розв’язувати обернені задачі до задач на різницеве порівняння двох часток; розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків. Вдосконалювати уміння будувати квадрат із заданою довжиною його сторони та обчислювати його периметр.

Розвивальна задача: розвивати логічне мислення учнів.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Сьогодні на уроці ми продовжимо вчитись додавати та віднімати багатоцифрові числа стовпчиком. На попередньому уроці ми переконались, що письмове додавання та віднімання багатоцифрових чисел виконується так само, як і трицифрових. Здогадайтесь, як діяти, коли треба додати три і більше багатоцифрових чисел. Чи правильні наші відповіді, перевіримо на цьому уроці.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 виконується учнями самостійно.

Учням, які швидше за інших виконали завдання, додатково:

Завдання №1 із робочого зошита виконується учнями самостійно.

2. Математичний диктант.

1) Запишіть числа: триста дев’ять тисяч чотири; п’ятдесят вісім тисяч п’ятдесят вісім. Підкресліть в кожному з них число першого класу однією рискою, другого класу – двома.

2) Запишіть числа, що містять: 203 одиниці першого класу та 456 одиниць другого класу; 63 одиниці першого класу а 890 одиниць другого класу. У кожному числі підкресліть розряд десятків одиниць однією рискою, десятків тисяч – двома.

3) Запишіть числа, що містять 4 сотні тисяч, 6 сотень та 4 одиниці; 7десятків тисяч 3 одиниці тисяч; 8 сотень. В кожному числі визначте загальну кількість десятків тисяч.

4) Запишіть числа, що містять: 23 одиниці першого класу та 5 одиниць другого класу; 804 одиниці другого класу та 26 одиниць першого класу. Замініть кожне число сумою розрядних доданків.

5) Знайти невідомий доданок, якщо значення суми 71000, а інший доданок 45000.

6) Знайти невідоме зменшуване, якщо значення різниці 56000, а від’ємник 17000.

7) Знайти невідомий від’ємник, якщо зменшуване 62000, а значення різниці 28000.

8) Число 43000 збільшити на 29000.

9) Число 81000 зменшити на 56000.

3. Актуалізація прийому письмового додавання. Актуалізація знання переставного закону додавання.

Завдання №2 виконується учнями біля дошки (у той час, поки решта класу виконує математичний диктант, двоє учнів працюють біля дошки).

4. Актуалізація письмового прийому додавання у випадку трьох доданків в межах 1000.

Завдання №3 виконується учнями біля дошки (під час математичного диктанту ще двоє учнів працюють біля дошки).

Після виконання математичного диктанту учні, що працювали біля дошки пояснюють класу власні розв’язання, а клас оцінює правильність міркувань та результатів.

 

ІІІ. ФОРМУВАННЯ НОВИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Перенесення способу міркування у випадку додавання трьох доданків у межах 1000 на випадки додавання трьох багатоцифрових чисел.

Завдання № 4 виконується колективно.

Учень біля дошки знаходить суму трьох доданків з коментарем: (підписую числа стовпчиком: пишу перший доданок, під ним другий – одиниці під одиницями, десятки під десятками, сотні під сотнями, підписую третій доданок – розряд під розрядом; додавання починаю з розряду одиниць, додаю одиниці, одержую 20 одиниць – це 2 десятки, тому під одиницями пишу 0, а 2 переходить до десятків; додаю десятки – буде 14 десятків та ще 2 десятки одержую 16 десятків – це 1 сотня та 6 десятків, пішу під десятками 6, 1 сотня переходить до сотень; додаю сотні – 10 сотень, та ще 1 сотня, буде 11 сотень – це 1 тисяча та 1 сотня, пишу ці числа у відповідних розрядах.)

Далі вчитель пропонує зіставити доданки суми, що розташовані у другому рядку стовпчика із доданками даної суми: і ; і . В кожній парі однакові числа першого класу, відмінність у тому, що в першому числі є ще й число другого класу. З’ясовуємо, як ця відмінність вплине на розв’язання. Чи допоможе нам виконане розв’язання для обчислення другої суми? У стовпчику, який вже записано на дошці, ліворуч від першого доданка дописуємо відповідне число другого класу, ліворуч від другого доданка – відповідне число другого класу. Визначаємо, що результати додавання одиниць, десятків та сотень в нас вже є, лишилося виконати додавання одиниць тисяч – 11 тисяч та ще 1 тисяча, яка перейшла від сотень, буде 12 тисяч – це 1 десяток тисяч та 2 тисячі, 2 тисячі пишемо під тисячами, а 1 десяток тисяч запам’ятовуємо. В першому доданку 4 десятки тисяч та ще 1 десяток тисяч, буде 5 десятків тисяч, пишемо у результаті у розряді десятків тисяч. Висновок: додавання трьох багатоцифрових чисел виконується так само, як і додавання трьох трицифрових чисел.

Аналогічно обчислюємо значення сум у другому стовпчику. Завдання виконується біля дошки з коментарем.

2. Первинне закріплення.

Завдання №2 із робочого зошита виконується з коментарем.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування вміння виконувати письмове додавання трьох доданків.

Завдання № 5 виконується з коментарем.

Звертаємо увагу учнів, що числа доцільно записувати у такий спосіб: спочатку число, що записуються найбільшою кількістю цифр, а потім з меншою кількістю цифр. Якщо у виразі доданок, що записаний меншою кількістю цифр стоїть на першому або другому місті, то доцільно переставити доданки у порядку зменшення кількості цифр у їх записі.

2. Формування навичок письмового віднімання багатоцифрових чисел.

Завдання №6 виконується учнями самостійно.

3. Дослідження залежності значення суми від зміни обох доданків.

Завдання №7 виконується колективно.

Актуалізуємо розуміння залежності значення суми від зміни одного з доданків: якщо один з доданків збільшиться (зменшиться) на кілька одиниць, то значення суми, так само, збільшиться (зменшиться) на стільки ж одиниць.

Пропонуємо учням прочитати перші доданки сум у першому стовпчику; помічаємо, що перший доданок весь час зменшується на 1, тому й значення суми, так само зменшується на один. Читаємо другі доданки сум, помічаємо, що другий доданок збільшується на 1, тому й значення суми також збільшується на 1. Отже, одночасно значення суми зменшується на 1 і збільшується на 1, отже значення суми не змінюється. Можна запропонувати учням перевірити це обчисленням. Отже, якщо один з двох доданків збільшиться на кілька одиниць, а інший зменшиться на стільки ж одиниць, то значення суми не зміниться. Використовуємо цей висновок для відповіді на поставлене запитання відповідно до сум другого стовпчика.

4. Оцінювання значення різниці.

Завдання №8 виконується колективно.

Дійсно, значення різниці буде більшим за 8000, тому що зменшуване містить 4 тисячі, а від’ємник менший за 4 тисячі.

Завдання №9 виконується колективно.

Щоб у числі змінилися лише цифри, що стоять в розряді одиниць і десятків треба віднімати двоцифрове число, яке менше або дорівнює 46.

5. Закріплення вміння розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків.

Завдання № 3 із робочого зошита – диференційована робота над задачею.

Звертаємо увагу учнів на те, що в цій задачі можна виконати пряму перевірку розв’язання, додавши знайдені числа, і якщо одержимо подане в тексті задачі значення суми трьох доданків, то впевнено можна стверджувати, що задачу розв’язано правильно.

6. Закріплення уміння креслити квадрат із заданими сторонами та уміння обчислювати периметр квадрата.

Що називається прямокутником? Що можна сказати про протилежні сторони прямокутника? Чи можна стверджувати, що будь-який прямокутник є квадратом; що будь-який квадрат є прямокутником? Дати означення квадрата. Чим відрізняється квадрат від будь-якого прямокутника? Пригадайте формулу периметра прямокутника. Якщо у квадрата всі сторони рівні, то як виглядатиме формула периметра квадрата? (Р = а * 4).

7. Розвиток логічного мислення учнів.

Завдання №11 виконується учнями колективно.

1) Якщо паркан стоїть уздовж дороги, то він не замкнений, тому проміжків між стовпами буде на 1 менше, ніж стовпів: 4 – 1 = 3. Якщо проміжок між стовпами 1 м, а таких проміжків 3, то довжина паркану: 1м * 3 = 3 м.

2) Якщо розпилюючи колоду зробили 4 розпили, то оцупків буде на 1 більше ніж розпилів: 4 + 1 = 5. Якщо довжина оцупка 1м, то довжина цілої колоди була: 1 м * 5 = 5 м

Зіставляємо задачі: містять одні й ті самі числа, але різні ситуації. Спільне в них те, що, на мові математики, є відрізок, який розбитий точками на частини: якщо рахувати кінці відрізка (дві точки), то кількість частин буде на 1 менше за кількість точок (задача 1), якщо не рахувати кінці відрізка, а лише внутрішні точки, то кількість частин буде на 1 більше кількості точок (задача 2).

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання № 6 виконати письмове віднімання та перевірити одержані результати, попередньо пригадавши правило перевірки правильності дії віднімання. Завдання №10 – розв’язати задачу, записавши її коротко у формі таблиці; для учнів з високими пізнавальними потребами, за бажанням - скласти і розв’язати хоча б одну обернену задачу.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Чи правильними були передбачення про виконання додавання багатоцифрових чисел? Що на уроці було зовсім новим? Що давалося легко? У чому потребуєте допомоги? Якими успіхами можете поділитися?

 

Урок №51 (с. 106 – 107)

Мета: формувати уміння розв’язувати задачі на знаходження трьох чисел за їх сумою і сумами двох доданків

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати навчальний досвід учнів відносно одиниць вимірювання маси і довжини та співвідношення між ними; способу заміни складеного іменованого числа простим, простого – складеним. Формувати вміння застосовувати письмовий прийом при додаванні і відніманні простих іменованих чисел. Актуалізувати прийоми письмового додавання та віднімання багатоцифрових чисел; перевірки правильності одержаного результату. Актуалізувати розуміння способу розв’язування задач на знаходження трьох чисел за їх сумою та сумами двох доданків, що містять трицифрові числові дані; застосування способу розв’язання до задач цього виду, що містять числові дані, подані багатоцифровими числами. Формувати уміння розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків. Вдосконалювати уміння знаходити значення виразів у кілька дій; застосовувати правило віднімання суми від числа, з’ясувати можливості тотожних перетворень математичних виразів на підставі даного правила. Вдосконалювати уміння розв’язувати рівняння, в яких права частина або один з компонентів поданий числовим виразом. Вдосконалювати навички письмового додавання та віднімання багатоцифрових чисел; перевірки одержаного результату; навички усного додавання і віднімання круглих багатоцифрових чисел.

 

Розвивальна задача: розвивати логічне мислення учнів.

 

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

У математиці трапляються задачі, в яких є певні шифри. Сьогодні нам доведеться «розшифрувати» секрети задач. Відзначте, чи доводилось вам зустрічатись у житті із подібними ситуаціями.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 із робочого зошита виконується учнями самостійно.

2. Усне опитування.

Дивись запитання до усного опитування до уроку №2.

3. Актуалізація способу дії з письмового додавання та віднімання.

У той час, поки відбувається усне опитування, чотири учні біля дошки виконують завдання №1. Після усного опитування, вони пояснюють виконані розв’язання, а решта учнів класу оцінює їх. Учні можуть ставити своїм товаришам додаткові запитання, користуючись запитаннями з усного опитування.

4. Актуалізація способу подання складеного іменованого числа у вигляді простого; простого іменованого числа у вигляді складеного.

Завдання №7,8 виконується з коментарем.

Перед виконанням завдань вчитель ставить запитання щодо одиниць вимірювання маси, довжини, та співвідношення між ними.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування уміння додавати і віднімати письмового прості іменовані числа, подані в одиницях вимірювання маси і довжини.

Завдання № 6 виконується з коментарем.

2. Закріплення способу міркування при розв’язуванні задач на знаходження трьох чисел за їх сумою та сумами двох доданків.

Завдання №2 виконується учнями колективно.

Вчитель нагадує, що на попередньому уроці було розв’язано задачу №3 із робочого зошита, і пропонує розглянути її короткий запис і визначити його особливості. Учні помічають, що є три ключові слова, є три шукані. Відомою є сума всіх трьох чисел та суми першого та другого шуканих чисел та другого та третього. Вчитель пропонує розглянути розв’язання цієї задачі: як знайти перше число? (треба від суми трьох чисел відняти суму другого та третього числа) як знайти третє число? (аналогічно – від суми трьох чисел відняти суму першого та другого числа) як знайти друге число? (треба або від суми першого та другого чисел відняти перше число або від суми другого та третього число відняти третє.)

Читаємо задачу 1. З’ясовуємо, що в ній так само три шукані і є три суми. Застосовуємо згаданий спосіб міркування і розв’язуємо задачу 1 лише на дошці.

Зазначимо, що можна не звертатися до матеріалу попереднього уроку, а після розв’язання задачі 1 поставити учням подані вище запитання.

Зіставляємо задачі 2 і 1. З’ясовуємо, що в них описується одна й та сама ситуація, містяться одній й ті самі шукані, навіть дані позначають однакові суми (за змістом), але числа інші. Якщо перекласти складені іменовані числа у прості, то одержимо багатоцифрові числа. Отже, зміна числових даних вплине на розв’язання задачі у такий спосіб, що у арифметичних діях братимуть участь відповідні багатоцифрові числа, а сам план розв’язування задачі не зміниться. Пропонуємо учням змінити записи на дошці так, щоб одержати розв’язання задачі 2. Можна обговорити з учнями можливість іншого способу при знаходження другого числа: знаходимо суму першого та третього числа і потім – від суми трьох чисел віднімаємо знайдену суму. Але треба мати на увазі, що цей спосіб міркування хоча і правильний, але не є раціональним.

Звертаємо увагу учнів на те, що в цій задачі можна виконати пряму перевірку розв’язання, додавши знайдені числа, і якщо одержимо подане в тексті задачі значення суми трьох доданків, то впевнено можна стверджувати, що задачу розв’язано правильно.

Узагальнюємо опорну схему задач на знаходження трьох чисел за їх сумою та сумами двох доданків та узагальнюємо спосіб міркування за пам’яткою.

3. Формування уміння розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків.

Завдання №3 виконується учнями самостійно.

4. Закріплення правила віднімання суми від числа; правила порядку дій у виразах. Формування обчислювальних навичок письмового додавання та віднімання багатоцифрових чисел.

Завдання №4 виконується колективно.

Зіставляючи вирази, учні помічають, що у їх записах містяться одні й ті самі числа; відмінність є лише у дужках. В першому виразі від числа 358253 віднімають і 16924 і 5722, а у другому – віднімають суму чисел 15924 та 5722. Пригадуємо правило віднімання суми від числа: щоб відняти суму від числа, достатньо від цього числа відняти один доданок, а потім другий доданок. Отже, ці вирази матимуть однакові результати. Учні перевіряють сформульоване твердження обчисленням: І варіант знаходить значення першого виразу, а ІІ – другого.

5. Вдосконалення вміння розв’язувати рівняння.

Завдання №5. Перше рівняння першого стовпчика – самостійна робота.

Другий стовпчик рівнянь пропонуємо учням з високим рівнем пізнавальних потреб і можливостей. Розв’язування виконується біля дошки.

6. Формування обчислювальних навичок.

Завдання № 2, 4 із робочого зошита виконується учнями самостійно.

7. Розвиток логічного мислення учнів.

Завдання № 2 на с. 127 виконується колективно.

Розв’язання задачі аналогічне до задачі №1 нв с. 127. Відповідь: у одній банці 2 кг цукру.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №7 – пригадати співвідношення між одиницями вимірювання маси та довжини і замінити складене іменоване число простим; №8 – замінити просте іменоване число складеним. Завдання № 3 із робочого зошита – розв’язати задачу.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Чи доводилось вам зустрічатись у житті із ситуаціями, описаними в задачах, які розв’язували? Яким же був «секрет» цих задач? Які завдання уроку потребують додаткового опрацювання? Чим у своїй роботі були задоволені?

 

Урок №52 (с. 108 – 109)

Мета: формувати обчислювальні навички.

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати прийоми письмового додавання та віднімання, способи перевірки одержаних результатів; способи заміни складеного іменованого числа простим, простого іменованого числа – складеним; письмовий прийом додавання і віднімання простих іменованих чисел. Створити та розв’язати проблемну ситуації, у наслідок якої відбудеться відкриття двох способів міркування при додаванні і відніманні складених іменованих чисел. Формувати навички додавання і віднімання складених іменованих чисел. Формувати уміння розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків; задачі, що містять збільшення або зменшення числа на кілька одиниць, сформульовані у непрямій формі.

Розвивальна задача: розвивати логічне мислення учнів (с. 127 №3).

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Розв’язуючи задачі на попередньому уроці ми опинилися в ситуації, коли треба було виконувати арифметичні дії зі складеними іменованими числами. Ви - діти кмітливі, тому й знайшли вихід із ситуації, замінивши складені іменовані числа простими. Але, виявляється, так діяти не обов’язково. Ви точно дещо знаєте, що допоможе виконувати дії з іменованими числами без їх перетворень.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 із робочого зошита виконується учнями самостійно.

2. Математичний диктант.

Запишіть відповідні математичні вирази і знайдіть їх значення:

1) Перший множник 23000, другий множник 4, знайти значення добутку.

2) Ділене 60000, дільник 4, знайти значення частки.

3) Число 85000 збільшити на 9000.

4) Число 45000 зменшити в 1000 разів.

5) На скільки число 48000 менше за 63000?

6) У скільки разів число 4200 більше за 3?

7) Зайти невідомий доданок, якщо значення суми 340000, а відомий доданок - 170000.

8) Знайти зменшуване, якщо значення різниці 48000, а від’ємник - 16000.

9) Знайти невідомий множник, якщо значення добутку 96000, а відомий множник - 8.

10) Знайти значення діленого, якщо значення частки 30000, а дільник - 12.

11) Знайти значення дільника, якщо ділене 510000, а значення частки – 3.

3. Актуалізація письмового прийому додавання та віднімання.

Завдання №1 виконується учнями біля дошки.

У той час, поки клас виконує математичний диктант, вчитель викликає до дошки кількох учнів. Після виконання математичного диктанту клас оцінює виконані розв’язання.

3. Актуалізація способу міркування при заміні складеного іменованого числа простим, простого – складеним.

Учитель ставить питання, аналогічні до наступних: Які основні величини ви знаєте? Назвіть одиниці вимірювання довжини у порядку збільшення. Скільки міліметрів у сантиметрі; у дециметрі; у метрі; у кілометрі? Яку частину дециметру становить 1 міліметр; сантиметр? Скільки сантиметрів у дециметрі; яку частину метру становить дециметр? Скільки метрів становить кілометр?

Завдання № 2, 3 виконуються усно колективно.

 

4. Актуалізація письмового додавання і віднімання простих іменованих чисел.

Завдання №4 виконується з коментарем.

 

ІІІ. ФОРМУВАННЯ НОВИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Ознайомлення зі способом письмового додавання і віднімання складених іменованих чисел.

Завдання №5 виконується колективно.

Учні читають вирази у кожному стовпчику. З’ясовуємо, як можна міркувати при обчисленні значення першого виразу? Зіставляємо перші доданки та другі доданки сум; зменшувані та від’ємник. Визначаємо, що ці числа рівні: у перших виразах стовпчиків записані прості іменовані числа, а у других –складені. Учні обчислюють значення першого виразу у першому стовпчику і, роблять висновок, що такий самий результат буде і у другому виразі стовпчика. Отже, щоб додати складені іменовані числа можна замінити їх простими, виконати додавання простих іменованих чисел стовпчиком. Аналогічно працюємо із виразами другого стовпчика і робимо відповідний висновок щодо віднімання складених іменованих чисел.

Далі розглядаємо і коментуємо розв’язання, подане у підручнику на с. 109. Звертаємо увагу на те, як підписані стовпчиком числа одних найменувань; спочатку виконується дія з числами менших найменувань, а потім – більших. При додаванні і відніманні чисел менших найменувань треба пам’ятати, скільки менших одиниць вимірювання міститься в більшій: при додаванні може статися, що треба виділити більшу одиницю вимірювання, і її слід врахувати при додаванні більших одиниць; при відніманні, якщо від менших одиниць зменшуваного не можна відняти менші одиниці від’ємника, потрібно позичити більшу одиницю та роздробити у менші, і це треба буде врахувати при відніманні більших одиниць вимірювання. Після коментування, учні ознайомлюються з пам’яткою, де подано два способи міркування: перший спосіб полягає у заміні складених іменованих чисел простими і додаванні або відніманні простих іменованих чисел з наступним поданням результату у вигляді складеного іменованого числа; другий - передбачає виконання обчислень зі складеними іменованими числами, починаючи з чисел менших одиниць.

 

2. Первинне закріплення.

Завдання №6 виконується з коментарем.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування вміння виконувати додавання та віднімання складених іменованих чисел двома способами.

Завдання № 2 із робочого зошита виконується учнями самостійно.

2. Вдосконалення уміння розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків.

Завдання № 7 виконується учнями самостійно.

3. Вдосконалення уміння розв’язувати задачі на збільшення або зменшення числа на кілька одиниць, сформульоване у непрямій формі.

Завдання № 3 із робочого зошита. Диференційована робота над задачею.

Звертаємо увагу учнів на те, що перша бригада відремонтувала на 78 м метрів, ніж друга, тому друга бригада відремонтувала на 78 м більше, ніж перша.

4. Розвиток логічного мислення учнів.

Завдання №3 с. 127 виконується колективно.

 

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання № 2 – замінити складене іменоване число простим; №3 – замінити просте іменоване число складеним. Завдання №6 виконати письмове додавання та віднімання складених іменованих чисел двома способами.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Про що нове ви дізнались сьогодні на уроці? Як слід підписувати складені іменовані числа, якщо необхідно виконати обчислення, не замінюючи ці числа простими іменованими? Як у цьому випадку слід міркувати? Що на уроці викликало складнощі? Яка робота давалася легко?

 

 

Урок №53 (с.110-111)

Мета: формувати обчислювальні навички

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати розуміння залежності значення суми від зміни одного з доданків, залежності значення різниці від зміни від’ємника. Актуалізувати прийом округлення при додаванні і відніманні; застосування прийому округлення до випадків додавання і віднімання, чисел, близькі до розрядних одиниць: 99,999,9999…. Формувати навички додавання та віднімання багатоцифрових чисел (за потреби – застосування прийомів раціональних обчислень). Формувати навички письмового додавання; дослідити закономірності у доданках (у першій сумі першого стовпчика – сума одиниць дорівнює 10, у другій – сума одиниць і сума десятків становить 10; у другому стовпчику в першому виразі – сума одиниць, сума десятків, сума сотень дорівнює 10; в другому виразі – сума одиниць, сума десятків, сума сотень, сума тисяч дорівнює 10), конструювати суми двох доданків, в яких простежується дана закономірність. Формувати навички письмового додавання та віднімання багатоцифрових чисел; перевірки одержаних результатів. Закріплювати письмові прийоми додавання і віднімання іменованих чисел. Формувати уміння обчислювати значення виразу зі змінною, що передбачає письмове додавання та віднімання багатоцифрових чисел.

 

Розвивальна задача: розвивати логічне мислення учнів під час «відкриття» раціонального способу додавання та віднімання чисел 99,999, 9999…, під час визначення закономірності сум і конструюванні сум, що мають цю саму закономірність.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Людині у повсякденному та у професійному житті часто доводиться виконувати обчислення із багатоцифровими числами. Скажіть, коли саме. Ми вже розглянули різні способи письмових обчислень. Між тим, іноді виписувати стовпчиком числа або натискати клавіші на калькуляторі довго. Математики придумали швидші способи обчислень, якими часто користуються дорослі, наприклад, під час купівлі товарів. Сьогодні і ви дізнаєтесь про нього.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 виконується учнями самостійно.

2. Усне опитування.

(Див. урок №3). Додатково: Назвіть лічильні одиниці (десяток, сотня, тисяча, десяток тисяч, сотня тисяч, мільйон). Які розрядні одиниці ви знаєте (10, 100, 1000, 10000, 10000)? Назвіть найбільше одноцифрове; двоцифрове; трицифрове; чотирицифрове; п’ятицифрове число (9, 99, 999, 9999, 99999). Назвіть найменше одноцифрове натуральне число; двоцифрове; трицифрове; чотирицифрове; п’ятицифрове; шестицифрове (1, 10, 100, 1000, 10000, 100000, 1000000). Яке число слідує в натуральному ряді за найбільшим одноцифровим число (найменше двоцифрове); за найбільшим трицифровим числом (найменше чотирицифрове число)… На скільки найбільше двоцифрове число менше за найменше трицифрове число (на 1); найбільше чотирицифрове за найменше п’ятицифрове число (на 1)…

3. Актуалізація розуміння залежності значення суми від зміни одного з доданків; значення різниці від зміни від’ємника.

Пригадуємо залежність значення суми від зміни одного з доданків (якщо один із доданків збільшиться на кілька одиниць, то значення суми також збільшиться на стільки ж одиниць); залежність значення різниці від зміни від’ємника (якщо від’ємник збільшиться на кілька одиниць, то значення різниці, навпаки, зменшиться на стільки ж одиниць).

Завдання №2 із робочого зошита.

4. Актуалізація способу дії при додаванні та відніманні чисел шляхом округлення одного з доданків або від’ємника. Застосування прийому округлення для додавання і віднімання чисел, близьких до розрядних одиниць.

Завдання №2 виконується колективно.

Коментар: 523 – 99. Від’ємник 99 замінюємо близьким круглим числом 100. Від 523 віднімемо 100. Визначаємо, на скільки більше віднімаємо, на 1, тому треба додати 1. Обчислюємо: 523 – 100 = 423; 423 + 1 = 424.

376 + 99. Другий доданок 99 замінюємо близьким круглим числом 100. До 376 додамо 100. Визначаємо, на скільки більше додамо, на 1, тому треба відняти 1. Обчислюю: 376 + 100 = 476; 476 – 1 = 375.

З’ясовуємо, які розрядні одиниці учні знають (10, 100, 1000, 10000, 100000, 1000000). Які числа близькі до розрядних одиниць (9, 99, 999, 9999, 99999), то у чому полягає спосіб міркування при додаванні та відніманні числа 9, 99, 999, 9999, 99999? Розглядаємо подані у підручнику правила.

 

ІІІ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Формування навичок додавання та віднімання багатоцифрових чисел.

Завдання №3 виконується учнями біля дошки. Пропонуємо учням обрати прийом обчислення: усний (округлення) чи письмовий (у стовпчик).

При розгляді розв’язувань із використанням прийому округлення звертаємо увагу учнів на те, що не лише числа 9, 99, 999, 9999, 99999 доцільно замінити розрядною одиницею, а й числа 98, 998, 9998… 97, 997, 9997…

Завдання №4 виконується колективно.

У виразі 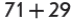сума одиниць становить 10, сума десятків дорівнює 10; результат розрядна одиниця 100. - у цьому виразі це й сума сотень дорівнює 10, одержимо розрядну одиницю 1000. - ще й сума тисяч дорівнює 10, буде 10000. - ще й сума десятків тисяч дорівнює 10, сума сотень тисяч дорівнює 10, маємо 1000000. Учні складають подібні суми.

Завдання №4 виконується учнями самостійно.

 

2. Формування навичок додавання та віднімання складених іменованих чисел.

Завдання №1 із робочого зошита виконується з коментарем.

Завдання № 8 виконується учнями самостійно.

Учні обирають зручний для них спосіб обчислення.

3. Вдосконалення уміння розв’язувати задачі на знаходження трьох чисел за сумою трьох та сумами двох доданків.

Завдання № 7. Диференційована робота над задачею.

Добираючи числові дані до задачі, учні мають розуміти, що сума трьох чисел має бути найбільшою. Після перевірки розв’язань, в яких використані різні групи числових даних, узагальнюємо ще раз спосіб розв’язування (див. с. 106 підручника).

4. Вдосконалення уміння розв’язувати задачі.

Завдання №8 виконується учнями самостійно.

1) 7: а; 2) 7: а * 5; 3) 21 * в; 4) 21 * х + 32 * у.

 

5. Розвиток логічного мислення учнів.

Спекотного дня 6 косарів випили діжку квасу за 8 годин. Дізнайтеся, скільки косарів за 4 години вип’ють таку саму діжку квасу.

1 спосіб (зведення до одиниці).

8 х 6 = 48 (годин) вип’є діжку квасу один косар.

48: 4 = 12 (косарів) – вип’ють діжку квасу за 4 години.

2 спосіб (на підставі взаємооберненої пропорційної залежності між величинами, спосіб відношень).

Якщо кількість годин скоротилася в 8: 4 = 2 рази, то кількість косарів, які вип’ють таку саме діжку квасу, збільшиться в 2 рази, тобто 6 х 2 = 12 (косарів).

Відповідь: 12 косарів.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №5 – виконати обчислення письмово, пригадавши не лише алгоритм письмового додавання й віднімання, а й письмового множення та ділення. Завдання №6 – обчислити значення виразів зі змінною; пропоную звернути увагу на результат другого виразу, а на наступному уроці ми обговоримо питання чому одержали саме такий результат. Завдання №8 – виконати додавання і віднімання складених іменованих чисел зручним для вас способом.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Що цікаве ви дізнались сьогодні на уроці? Як можна виконувати додавання та віднімання чисел, близьких до розрядної одиниці 9,99,999,9999, 99999, 98, 998…? Що ще зацікавило вас на уроці? Що треба мати на увазі добираючи числові дані до задач, в яких шуканими є три числа і дано три суми: суму трьох доданків, суму першого та другого, суму другого та третього? Розкажіть про результати власних навчальних досягнень: що вдалося; що викликає труднощі.

 

Урок №54 (с.112 – 113)

Мета: формувати обчислювальні навички

Дидактичні задачі. Вдосконалювати навички усних обчислень; уміння знаходити значення виразу зі змінною. Формувати уміння розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків; задачі на знаходження суми двох добутків та на різницеве порівняння двох добутків; складені задачі, які містять збільшення числа у кілька разів, сформульоване у непрямій формі. Вдосконалювати навички усних та письмових обчислень. Закріплювати розуміння залежності значення суми від зміни одного з доданків. Вдосконалювати уміння розв’язувати рівняння, в яких один з компонентів або права частина подана числовим виразом.

 

Розвивальна задача: розвивати логічне мислення учнів при ознайомленні з алгебраїчним методом розв’язування задач на знаходження трьох чисел за їх сумою та сумами двох доданків; при відновленні істинних рівностей, при розв’язуванні подвійних нерівностей.

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Сьогодні на уроці спробуйте якнайбільше завдань робити самостійно. Це допоможе вам зрозуміти, що засвоїли з успіхом, а над чим ще доведеться попрацювати.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Усна лічба.

Завдання №1 виконується учнями самостійно.

2. Математичний диктант.

1) Тетянка купила 5 наборів олівців по 27 гривень. Скільки грошей вона має сплатити за покупку.

2) Дід Сашко виготовив 54 сопілки для малечі, виготовляючи по 3 сопілки щодня. Скільки днів працював дід Сашко?

3) Оленка з подружками вишили 36 серветок за 3 дні. Скільки серветок щодня вишивали дівчатка?

4) Простий олівець коштує 8 гривень, а механічний олівець коштує 32 гривні. У скільки разів дешевший простий олівець за механічний?

5) Машина щогодини долає по 90 км. Скільки кілометрів проїде машина за 4 години руху?

6) Миколка пройшов 370 м і йому залишилося пройти до школи ще у тричі більше. Скільки метрів залишилося пройти до школи Миколці.

7) Альбом коштує 27 гривень, а набір для творчості у 6 разів дорожчий. Скільки коштує набір для творчості.

8) Софійка на велосипеді проїхала 1800 м, долаючи щосекунди по 5 м. Знайди час руху дівчинки.

ІУ. ФОРМУВАННЯ ВМІНЬ І НАВИЧОК. ЗАКРІПЛЕННЯ ВИВЧЕНОГО

1. Вдосконалення вміння знаходити значення виразів зі змінною; вдосконалення обчислювальних навичок.

Завдання №2 виконується біля дошки.

Після знаходження значення другого виразу, зіставляємо цей вираз (а саме його частину до останньої дії) та вираз, що пропонувався для домашньої роботи, і з’ясовуємо, чому в результаті обчислень – додавання та віднімання певного числа, одержуємо число, яке стоїть у виразі першим. Доходимо висновку: якщо до числа одночасно додати та відняти одне й те саме число, то це число не зміниться. Учні, які ще на етапі виконання домашнього завдання це помітили, можуть відразу переходити до останньої дії при знаходження значення другого виразу.

2. Вдосконалення вміння розв’язувати задачі на знаходження трьох чисел за їх сумою та сумами двох доданків.

Завдання №3 виконується учнями самостійно.

Учні, які виконали роботу раніше за решту класу, під керівництвом вчителя пояснюють, подане у підручнику розв’язання задачі алгебраїчним методом. Зазначимо, що при розв’язування задач цього виду через складання рівняння, доцільне число, яке входить у обидві суми двох доданків замінити змінною; виразити інші доданки цих двох сум через змінну; записати суму всіх трьох чисел та її значення, у такий спосіб склавши рівняння. Для розв’язування рівняння треба скористатися попереднім висновком: якщо до числа додати, а потім відняти одне й те саме число або відняти, а потім додати одне й те саме число, то дане число не зміниться, маємо:

390 + 310 – х = 530

700 – х = 530

Х = 700 – 530

Х = 170 - 170 кг борошна на рогалики;

390 – 170 = 220 (кг) борошна на батони;

310 – 170 = 140 (кг) борошна на калачі.

Перевірка: 170 + 220 + 140 = 530 (кг) всього на всі вироби.

 

3. Вдосконалення уміння ставити запитання до даної умови відповідно до виразу.

Читаємо перший вираз. Пояснюємо, що означає кожне число у виразі; що означають добутки 30 і 15 та 40 і 15. З’ясовуємо, що перший вираз є сумою двох добутків. Тому запитуватись має «Скільки всього тюльпанів?». Обчислюємо значення виразу та відповідаємо на поставлене запитання. Другий вираз являє собою різницю двох добутків. Тому, виходячи з поданої умови, можна запитати «На скільки більше (менше)…?». Обчислюємо значення виразу і відповідаємо на поставлене запитання.

4. Вдосконалення обчислювальних навичок додавання та віднімання багатоцифрових чисел.

Завдання №6, 8. Робота за сходинками складності.

І сходинка складності – обчислити значення виразів №6, застосовуючи письмовий прийом.

ІІ сходинка складності – обчислити значення виразів застосовуючи усний прийом та пояснити, чому так можна міркувати.

ІІІ сходинка – виконати завдання №8 і довести свою думку.

5. Розвиток варіативного мислення учнів.

Завдання №7 виконується колективно.

Перше завдання не являє жодних труднощів, оскільки виконується додавання стовпчиком. Останнє завдання має не один правильний розв’язок.

Завдання № 9 виконується колективно.

Учні називають числа, що більші за 45728; підставляємо кожне число замість змінної у нерівність і читаємо нерівність зліва направо та справа наліво, наприклад 45729 більше за 45728; 45728 менше за 45729. Аналогічно працюємо над другою нерівністю першого стовпчика, в якій маємо дібрати числа, які більші за 6708.

Нерівності другого стовпчика цікаві тим, що число, яке маємо дібрати одночасно більше деякого числа і менше певного числа. Наприклад, число р більше за 45720, але менше за 45725. Розв’язуючи цю нерівність, учні фактично відтворюють відрізок натурального ряду, який обмежений даними числами: 45721, 457222, 45723, 45724. Аналогічно працюємо на другою нерівністю другого стовпчика.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №5 – розв’язати задачу, скориставшись підказкою. Треба звернути увагу на запитання: «Скільки ще комах принесла синичка протягом дня?». Перед відповіддю на це запитання доцільно пояснити кожний відрізок на схемі. Рожевий відрізок означає кількість комах, що принесла синичка вранці, що в 5 разів менше, ніж всього комах протягом дня; тому протягом дня вона принесла в 5 разів більше. Отже, зелений відрізок означає скільки всього комах принесла синичка всього протягом дня. Шуканою є різниця між загальною кількістю комах, що принесла синичка протягом дня та тією кількістю комах, що вона принесла вранці. Завдання №10 – розв’язати рівняння. Завдання № 1 із робочого зошита – виконати додавання та віднімання застосувавши усний або письмовий прийом.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Які враження ви маєте від своєї роботи? Що в своїй роботі вам подобається? Що хотілося б змінити?

 

Урок №55

Мета: формувати уявлення про швидкість руху тіла.

Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати уміння розв’язувати прості задачі з величинами: продуктивність праці, час роботи, загальний виробіток на знаходження продуктивності праці; у дослідженні задачі змінити ситуації (зміна величин) й одержати задачу з описом процес руху тіла, в якій шуканою є кількість кілометрів, що долає об’єкт за одиницю часу; дослідити вплив цієї зміни на розв’язання задачі; ознайомити з поняттям швидкості руху тіла, одиницями швидкості та формулою швидкості. Зді