Методичні вказівки до рішення типових задач
Задача 1. Визначення помилки вибіркової середньої при випадковому безповторному та механічному виборі.
В районі проживає 2800 сімей. Для встановлення середньої кількості дітей в сім'ї була проведена 5% випадкова безповторна вибірка сімей. В результаті обстеження було отримано такі дані.
| Кількість дітей | ||||||||
| Кількість сімей |
З ймовірністю 0,950 необхідно визначити межі, в яких буде знаходиться середня кількість дітей в сім'ї у генеральній сукупності району. Зробити висновки.
Розв’язання
Для визначення меж генеральної середньої, необхідно розрахувати вибіркову середню та помилку вибіркової середньої. Встановимо середню кількість дітей у сім'ї у вибірковій сукупності та дисперсію вибірки.
Таблиця – Розрахунок вибіркової середньої та вибіркової дисперсії
Кількість
дітей у сім'ї ( ) )
| Кількість
сімей, 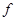
| 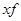
| 
| ( )2 )2
| 
|
| -2,6 | 6,76 | 121,68 | |||
| -1,6 | 2,56 | 92,16 | |||
| -0,6 | 0,36 | 8,64 | |||
| 60 | 0,4 | 0.16 | 3 2 | ||
| 60 | 1,4 | 1,96 | 29,40 | ||
| 2,4 | 5,76 | 57,60 | |||
| 3,4 | 11,56 | 104,04 | |||
| 4,4 | 19,36 | 154,88 | |||
| Всього | х | х | 571,60 |
Вибіркова середня: 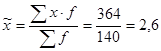 дітей.
дітей.
Вибіркова дисперсія: 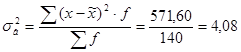 .
.
Середня квадратична помилка вибірки відносно середньої при безповторному відборі складає:
 .
.
Заданій ймовірності Р=0,950 відповідає коефіцієнт довіри t = l,96. Тоді гранична помилка вибірки складає
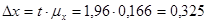 дітей.
дітей.
Довірчий інтервал для генеральної середньої
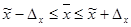
 .
.
З ймовірністю 0,95 або 95% середня кількість дітей в сім'ї району знаходиться в межах
2 
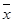
 3
3
Задача 2. Визначення необхідної чисельності вибірки при вивченні середньої для простого випадкового та механічного відбору.
В районі проживає 2800 сімей. У випадку простої безповоротної вибірки необхідно визначити середній розмір вибірки при умові, що помилка вибіркової середньої не повинна перевищувати 0,325 сім`ї з ймовірністю Р = 0,950 і середньому квадратичному відхиленні 2,02 сім'ї. Зробити висновки.
Розв’язання
У випадку безповторного відбору необхідна чисельність вибірки розраховується:
 .
.
При заданій ймовірності Р = 0,950 коефіцієнт довіри t становить 1,96. При чисельності генеральної сукупності N = 2800 сімей, граничної помилки вибірки відносно середньої 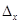 = 0,325 сім`ї та середньому квадратичному відхиленні
= 0,325 сім`ї та середньому квадратичному відхиленні 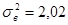 сім’ї визначимо необхідну чисельність вибірки:
сім’ї визначимо необхідну чисельність вибірки:
 сім`ї
сім`ї
Для порівняння визначимо чисельність вибірки у випадку повторного випадкового відбору, який використовується при відсутності даних чисельності генеральної сукупності:
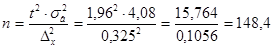 сім`ї.
сім`ї.
В даному випадку існує певна розбіжність, що свідчить про те, що безповторна вибірка приводить до більш точних результатів.
Задача 3. Визначення помилки при випадковому безповторному відборі методом малої вибірки
На дослідних ділянках висіяні нові сорти озимої пшениці. Для визначення очікуваної врожайності взято випадково 10 дослідних ділянок. Дані про врожайність на цих ділянках показано в таблиці.
| № ділянки | ||||||||||
| Урожайність, ц/га | 45,4 | 48,0 | 47,4 | 45,6 | 43,9 | 44,8 | 46,4 | 49,2 | 47,8 | 51,5 |
Потрібно визначити:
- середню врожайність пшениці;
- середню та граничну помилки вибіркової середньої (коефіцієнт довіри t = 2,26);
- межі в яких з ймовірністю 0,954 перебуває середня урожайність у генеральній сукупності.
Зробити висновки.
Розв’язання
Для находження середньої врожайності пшениці та дисперсії вибіркової сукупності скористаємось допоміжною таблицею.
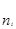
| 
|  – – 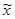
| ( – – 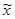 )2 )2
|
| 45,4 | -1,6 | 2,56 | |
| 48,0 | 1,00 | ||
| 47,4 | 0,4 | 0,16 | |
| 45,6 | -1,4 | 1,96 | |
| 43,9 | -3,1 | 9,61 | |
| 44,8 | -2,2 | 4,84 | |
| Продовження таблиці | |||
| 46,4 | -0,6 | 0,36 | |
| 49,2 | 2,2 | 4,84 | |
| 47,8 | 0,8 | 0,64 | |
| 51,5 | 4,5 | 20,25 | |
| Разом | 470,0 | х | 46,22 |
1. Середнє значення врожайності пшениці
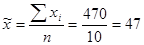 ц/га
ц/га
За даними таблиці обчислюємо вибіркову дисперсію

2. Середня квадратична помилка вибірки дорівнює
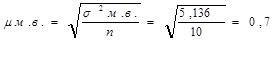 ц/га
ц/га
Отже, значення вибіркової середньої `х = 47 ц/га є оцінкою генеральної середньої з середньою помилкою 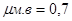 ц/га
ц/га
При заданому рівні ймовірності p = 0,954 коефіцієнт довіри (t) при малій вибірці відповідно до математичних таблиць розподілу Стюдента складає:
t = 2,26 при рівні значущості λ  = 0,05 та числі ступенів вільності к = n-1 = 10-1=9
= 0,05 та числі ступенів вільності к = n-1 = 10-1=9
Тоді гранична помилка вибірки дорівнює:
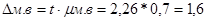 ц/га
ц/га
3. Проведемо інтервальну оцінку середньої врожайності пшениці в генеральній сукупності:
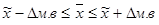 ,
,
47,0 – 1,6 ≤  ≤ 47,0 + 1,6
≤ 47,0 + 1,6
45,4 ≤  ≤ 48,6.
≤ 48,6.
Висновок: З заданою ймовірністю P = 0,954 можна стверджувати, що середня врожайність пшениці в генеральній сукупності перебуває в інтервалі від 45,4 ц/га до 48,6 ц/га.
Тема 12. Графічний метод
План семінару:
1. Дайте визначення статистичного графіка.
2. Які є види статистичних графіків?
3. Діаграми, як спосіб графічного відображення статистичних даних. Види діаграм.
4. Графіки порівняння та динаміки.
5. Графіки структури та взаємозв’язку.
Література: [1,5,9,11,12].
Зміст:
1. Мета і завдання практичних занять
2. Зміст дисципліни
3. Список літератури
4. Методичні вказівки до проведення семінарських занять і вирішення
типових задач






