Вы можете задаваться вопросом: а откуда мы знаем, что написанное выше —
правда? В конце концов, какая разница между «существует 75-процентная
вероятность увидеть кошку под столом» и «существует 75-процентная веро-
ятность того, что кошка находится под столом». Трудно вообразить экспери- 
Часть III. Энтропия и ось времени
мент, который мог бы провести различие между этими вероятностями; в конце
концов, единственный способ узнать, где кошка, — посмотреть в ее любимых
местах. Однако существует критически важное явление, благодаря которому
суть различия становится очевидной. Это квантовая интерференция. Чтобы
понять, что это значит, придется запастись терпением и углубиться в детали
того, как в действительности работают волновые функции.
В классической механике, где для описания состояния частицы указывают
ее положение и импульс, об этом состоянии можно думать как о наборе чисел.
Для одной частицы в обычном трехмерном пространстве необходимо указать
шесть чисел: положение в каждом из трех направлений и импульс в каждом из
трех направлений. В квантовой механике состояние описывается волновой
функцией, которую также можно представлять себе как набор чисел. Задача
этих чисел — сообщать нам для любого наблюдения или измерения, которое
нам только вздумается выполнить, какова вероятность того, что мы получим
определенный результат. Таким образом, казалось бы, совершенно естествен-
но полагать, что необходимые нам числа — это самые обыкновенные вероят-
ности: вероятность того, что мы увидим Китти на диване, вероятность того,
что мы увидим Китти под столом, и т. д.
Выясняется, однако, что это работает совсем не так. Волновые функции
на самом деле схожи с волнами: типичная волновая функция колеблется
в пространстве и времени подобно волне на поверхности пруда. Это не со-
всем очевидно в нашем простом примере, предусматривающем только два
возможных результата наблюдений: «на диване» и «под столом». Но если
рассмотреть наблюдения с непрерывным множеством возможных исходов,
например наблюдение за положением реальной кошки в реальной комнате,
то многое сразу же прояснится. Волновая функция похожа на волну на по-
верхности пруда; единственная разница в том, что это волна в пространстве
всех возможных результатов наблюдения: например, всех возможных поло-
жений в комнате.
Когда мы видим реальную волну, то замечаем, что относительно поверх-
ности пруда в спокойном состоянии высота воды в волне в разных местах
разная. Где-то она выше уровня спокойной воды, а где-то она опускается ниже.
Для того чтобы описать волну математически, мы могли бы с каждой точкой
пруда связать амплитуду — уровень воды относительно поверхности непо-
тревоженной водной глади. В одних местах амплитуда будет положительной,
в других — отрицательной. Волновые функции в квантовой механике работа-
ют точно так же. С каждым возможным результатом наблюдения волновая
функция связывает число, которое мы называем амплитудой и которое может 
Глава 11. Квантовое время
быть положительным или отрицательным. Полная волновая функция состоит
из определенной амплитуды для каждого возможного результата наблюдения;
это и есть числа, описывающие состояние в квантовой механике аналогично
положениям и импульсам, которые описывают состояние в классической ме-
ханике. Существует амплитуда, соответствующая пребыванию Китти под
столом, и еще одна амплитуда, соответствующая нахождению ее на диване.
При таких условиях у нас остается только одна нерешенная проблема: мы
говорим о вероятностях, а вероятность наступления какого-то события никог-
да не может быть отрицательным числом. Таким образом, нельзя утверждать,
что амплитуда, связанная с определенным результатом наблюдения, дает веро-
ятность наступления этого результата; вместо этого должен существовать
способ вычисления вероятности, основанный на известном значении ампли-
туды. К счастью, расчет очень прост! Для того чтобы получить вероятность,
нужно взять амплитуду и возвести ее в квадрат:
(вероятность увидеть X) = (амплитуда, связанная с X)2.
Таким образом, если волновая функция Китти связывает амплитуду 0,5
с возможностью увидеть кошку на диване, вероятность на самом деле увидеть
ее там равняется (0,5)2 = 0,25, или 25 %. Принципиально важно то, что значение
амплитуды могло бы быть отрицательным, то есть –0,5, и мы все равно полу-
чили бы тот же самый ответ: (–0,5)2 = 0,25. Это может казаться бессмысленным
излишеством — две разные амплитуды соответствуют одной и той же физиче-
ской ситуации, однако выясняется, что наличие положительных и отрицатель-
ных значений играет ключевую роль в эволюции состояний в квантовой меха-
нике.4
Интерференция
Теперь, когда нам известно, что волновые функции могут связывать отрица-
тельные амплитуды с возможными результатами наблюдений, можно вернуть-
ся к вопросу, почему мы вообще заговорили о волновых функциях и суперпо-
зициях, вместо того чтобы просто приписать вероятности разным исходам.
Причина кроется в интерференции, и эти отрицательные значения необходи-
мы для того, чтобы разобраться, откуда она берется. Мы можем сложить две
(отличные от нуля) амплитуды и получить нуль, что было бы невозможно, если
бы амплитуды никогда не принимали отрицательные значения.
Для того чтобы понять, как это работает, давайте немного усложним нашу
модель кошачьей динамики. Представьте себе, что мы видим, как Китти выходит 
Часть III. Энтропия и ось времени
из спальни на втором этаже. Благодаря нашим предыдущим наблюдениям за ее
перемещениями по дому мы собрали достаточно много сведений о том, как
действует эта квантовая кошка. Мы знаем, что, стоит ей спуститься на первый
этаж, она неминуемо окажется либо на диване, либо под столом и нигде больше
(то есть ее конечное состояние представляет собой волновую функцию, опи-
сывающую суперпозицию пребывания на диване и пребывания под столом).
Однако предположим также, что нам известно о существовании двух возмож-
ных путей, ведущих от кровати на втором этаже до одного из мест отдыха на
первом этаже: Китти сделает остановку либо у миски с кормом, чтобы под-
крепиться, либо у когтеточки, чтобы поточить когти. В реальном мире для
описания всех этих возможностей достаточно классической механики, но
в нашем идеализированном мире мысленного эксперимента мы считаем, что
квантовые эффекты играют важную роль.
Теперь посмотрим, какие результаты в действительности дает наше наблю-
дение. Мы проведем эксперимент двумя разными способами. Во-первых,
увидев Китти на первом этаже, мы будем тихонечко следовать за ней, для того
чтобы увидеть, по какому маршруту она пойдет: мимо миски с кормом или
мимо когтеточки. Вообще-то у нее есть волновая функция, описывающая су-
перпозицию обеих возможностей, но когда мы проводим фактический экспе-
римент, мы всегда получаем конкретный результат. Мы ведем себя тише воды
ниже травы, и кошка нас совсем не замечает; если хотите, можете даже вооб-
разить, что мы оснастили весь дом шпионскими камерами или лазерными
датчиками. Совершенно не важно, с помощью какой технологии мы выясняем,
подходит Китти к миске или к когтеточке; главное, что мы пронаблюдали это
действие.
Мы обнаруживаем, что Китти останавливается у миски ровно в половине
случаев и точно так же в половине случаев делает остановку у когтеточки (для
того чтобы максимально упростить условия, мы предполагаем, что на своем
пути к месту отдыха она посещает либо одно место, либо другое, но никогда
оба). Ни одно наблюдение, разумеется, само по себе не выявляет волновую
функцию; оно позволяет лишь сказать, что в этот конкретный раз мы увидели
кошку либо у когтеточки, либо у миски. Но представьте себе, что мы повторя-
ем этот эксперимент очень много раз, и это дает нам возможность делать обо-
снованные выводы относительно вероятностей этих двух событий.
Однако мы не останавливаемся на этом. Мы позволяем Китти продолжить
путь либо на диван, либо под стол, и после того как она устраивается на отдых,
мы снова смотрим, какое же место она выбрала. Этот эксперимент мы также
повторяем достаточное количество раз, для того чтобы определить вероят- 
Глава 11. Квантовое время
ности. Теперь мы обнаруживаем, что совершенно неважно, останавливалась
она у когтеточки или у миски с кормом; в обоих ситуациях мы видим, что
ровно в половине случаев она в итоге приходит на диван, а в половине — под
стол, и выбор итогового места отдыха абсолютно не зависит от того, шла она
к нему через миску с едой или когтеточку. Очевидно, промежуточный шаг на
этом маршруте не играет особой роли; вне зависимости от того, где кошка
делает остановку в пути, волновая функция в конце дает равные вероятности
для дивана и для стола.
А теперь начинается самое интересное. На этот раз мы вообще не будем
смотреть, какой промежуточный шаг Китти делает на своем пути к дивану или
столу; нам неинтересно, останавливается она у когтеточки или у миски с кормом.
Мы просто ждем, когда она устроится на диване или под столом, а затем про-
веряем, где она, восстанавливая итоговые вероятности, полученные из волно-
вой функции. Какого результата следует ожидать?
В мире, где царит классическая механика, мы знаем, что должны увидеть.
Когда мы шпионили за кошкой, мы были очень осторожны, чтобы наше на-
блюдение не повлияло на ее действия, и в половине случаев мы обнаруживали
ее на диване, а в половине — под столом, независимо от того, по какому марш-
руту она двигалась. Очевидно, что даже если мы не видим, чем она занимается
по пути, это не должно играть никакой роли: в любом случае на последнем шаге
у нас есть два исхода с равными вероятностями. Таким образом, даже не на-
блюдая за промежуточным этапом, мы все равно должны получать одинаковые
значения вероятности.
Однако все совсем не так. Это не то, что мы видим в нашем идеализирован-
ном мире мысленного эксперимента, где кошка — это настоящий квантовый
объект. Когда мы решаем не смотреть, останавливается Китти по пути у миски
с едой или у когтеточки, оказывается, что в 100 % случаев в конце она устраи-
вается на отдых на диване! Мы никогда не обнаруживаем ее под столом, то есть
финальная волновая функция связывает с этим возможным результатом нулевую
амплитуду. Очевидно, что если все это правда, то именно наличие шпионских
камер кардинальным образом изменило волновую функцию кошки. Возможные
варианты перечислены в таблице ниже. 
|
Часть III. Энтропия и ось времени
И это вовсе не исключительно мысленный эксперимент; такой опыт дей-
ствительно проводился. Не на настоящих кошках, которые, несомненно, от-
носятся к макроскопическим объектам и хорошо описываются в классическом
пределе, а на отдельных фотонах в ходе эксперимента, известного под названи-
ем «эксперимент с двойной щелью». Есть две щели, через которые может
пролететь фотон, и если мы не наблюдаем, через какую щель он пролетает, то
получаем одну волновую функцию, а если наблюдаем, то совершенно другую,
независимо от того, насколько осторожным и ненавязчивым был контроль.
Вот как это все объясняется. Представим себе, что мы решили проследить,
где Китти делает остановку — у миски или у когтеточки, и видим, что она
остановилась у когтеточки. Завершив свои дела у когтеточки, она эволюцио-
нирует в суперпозицию, где пребывание на диване и пребывание под столом
равновероятны. В частности, вследствие особенностей начального состояния
Китти и определенных аспектов квантовой кошачьей динамики итоговая вол-
новая функция связывает равные положительные амплитуды с «диваном»
и «столом». Теперь рассмотрим другой вариант промежуточного этапа, когда
мы видим, что кошка останавливается у миски с едой. В данном случае итоговая
волновая функция связывает отрицательную амплитуду со столом, а положи-
тельную с диваном — это равные, хотя и противоположные по знаку значения,
и, следовательно, соответствующие вероятности абсолютно одинаковы.5
Однако если мы не наблюдаем за кошкой и не видим ее на промежуточном
этапе — у когтеточки или миски, тогда (в соответствии с природой нашего
эксперимента) на этом промежуточном шаге она находится в суперпозиции
двух возможностей. В такой ситуации правила квантовой механики предписы-
вают нам сложить два возможных вклада в итоговую волновую функцию: один
для маршрута, где Китти останавливается у когтеточки, и второй для маршру-
та, включающего миску с едой. В обоих случаях амплитуды, соответствующие
завершению маршрута на диване, имели положительные значения; таким об-
разом, они усиливают друг друга. Но амплитуды для маршрутов, заканчиваю-
щихся под столом, были противоположными по знаку в зависимости от про-
межуточного шага. То есть при сложении они сокращают друг друга. По
отдельности маршруты с любым из двух возможных промежуточных шагов
давали нам ненулевую вероятность того, что в конце пути Китти устроится на
отдых под столом, но когда одновременно допустимы оба пути (потому что мы
не смотрим, по какому она решила пойти), амплитуды интерферируют.
Вот почему волновые функции должны включать отрицательные значения
и вот откуда мы знаем, что волновые функции — это «реальные» вещи, а не
просто какие-то бухгалтерские инструменты для отслеживания вероятностей. 
Глава 11. Квантовое время
(+)
(+)
(-)
(+)
(0)
(+)
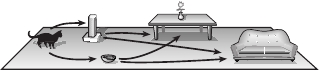
Рис. 11.1. Альтернативные пути эволюции волновой функции Китти. На верхней картин-
ке мы видим, что она остановилась у когтеточки, после чего пойдет либо под стол, либо
на диван — у обеих этих возможностей положительные амплитуды. На картинке в центре
мы видим, что она подошла к миске с кормом, а оттуда также может отправиться либо под
стол, либо на диван, но на этот раз со столом связана отрицательная амплитуда (хотя ве-
роятность все так же больше нуля). Нижняя картинка соответствует ситуации, когда мы
не отслеживаем промежуточный шаг ее маршрута, поэтому складываем амплитуды двух
допустимых возможностей. В результате мы получаем нулевую амплитуду для стола (так
как положительный и отрицательный вклады сокращают друг друга) и положительную
амплитуду для дивана
Мы рассмотрели явный случай, когда все вероятности положительны, но ито-
говая волновая функция получает вклады от двух разных промежуточных шагов,
которые сокращают друг друга.
Давайте остановимся на секунду и насладимся тем, насколько глубокомыс-
ленно все это выглядит с нашей традиционной точки зрения, зараженной
предубеждениями классической механики. Для каждой конкретной реализации
эксперимента нам кажется логичным задать вопрос: так где же Китти сделала
остановку — у миски с кормом или у когтеточки? Единственный допустимый
ответ на этот вопрос — нигде. Она не останавливалась ни там, ни там. Она
находилась в суперпозиции обеих возможностей, и нам это известно, потому 
|
|
|
Часть III. Энтропия и ось времени
что обе возможности оказали значительное влияние на амплитуду окончатель-
ного ответа.
Реальные кошки — это суетливые макроскопические объекты, состоящие
из очень большого числа молекул, и их волновые функции обычно резко лока-
лизуются вокруг того, что очень напоминает наше классическое понятие «по-
ложения в пространстве». Но на микроскопическом уровне все эти разговоры
о волновых функциях, суперпозициях и интерференции становятся до преде-
ла наглядными. Квантовая механика поначалу кажется чем-то жутко непонят-
ным, но это самая суть того, как работают механизмы Природы.
Коллапс волновой функции
Во всех подобных обсуждениях есть одна вещь, очень часто сбивающая людей
с толку и заставляющая — хотя и из лучших побуждений — пойти по ложному
следу. Это ключевая роль, выпавшая на долю наблюдений. Когда мы наблюдали
за тем, какой выбор кошка делала на пересечении дорожек, ведущих к когтеточ-
ке и миске, то получали один ответ для конечного состояния, когда же не делали
никаких наблюдений, то совершенно иной. Но физика не должна так работать!
Мир должен эволюционировать согласно законам Природы, и неважно, наблю-
даем мы за этим процессом или нет. Да и вообще, что можно считать «наблюде-
нием»? Что, если мы установим везде камеры наблюдения, но никогда не будем
просматривать пленки? Будет ли это считаться наблюдением? (Да, будет.) И что
именно происходит, когда мы наблюдаем за экспериментом?
Это очень важные вопросы, ответы на которые не совсем очевидны. В на-
учном сообществе физиков не существует единого мнения ни относительно
того, что можно считать наблюдением (или «измерением») в квантовой меха-
нике, ни относительно того, что происходит, когда наблюдение осуществляет-
ся. Это так называемая проблема измерения, попытки решить которую — ос-
новное занятие множества людей, проводящих время в размышлениях об
интерпретации квантовой механики. Подобных интерпретаций существует
уже немало, но мы с вами обсудим только две из них: более или менее стандарт-
ную картину, известную под названием «копенгагенская интерпретация»,
и взгляд, кажущийся (мне) заслуживающим большего уважения и лучше от-
ражающим реальное положение вещей, который носит пугающее название
«многомировая интерпретация». Давайте сперва познакомимся с копенгаген-
ской интерпретацией.6
Такое название эта интерпретация носит потому, что Нильс Бор, ученый,
который во многих отношениях может считаться крестным отцом квантовой 
Глава 11. Квантовое время
механики, помогал в ее разработке в своем институте в Копенгагене в 1920-е годы.
Настоящая история этой точки зрения сложна, и точно известно, что огромный
вклад в ее развитие внес Вернер Гейзенберг, еще один пионер квантовой меха-
ники. Но нас сейчас интересует не столько история, сколько статус копенгаген-
ской интерпретации как некоего эталона, как он подается во всевозможных
учебниках. Каждому физику приходится сначала познакомиться с этой точкой
зрения, и лишь затем ему выпадает возможность рассмотреть альтернативы (или
отказаться от их рассмотрения — бывает по-разному).
Копенгагенская интерпретация квантовой механики настолько же проста
в формулировке, насколько сложна в понимании: когда квантовая система под-
вергается измерению, ее волновая функция коллапсирует 7. То есть волновая
функция мгновенно изменяется, превращаясь из описания суперпозиции раз-
личных возможных результатов наблюдения в совершенно другую волновую
функцию, которая отвечает 100-процентной вероятности результата, который
был получен при фактическом измерении, и 0-процентной вероятности каких-
либо других результатов. Такой тип волновой функции, полностью сконцен-
трированной на единственном возможном результате наблюдения, называется
«собственным состоянием». Стоит системе перейти в собственное состояние,
и, продолжая выполнять те же наблюдения, вы будете получать тот же самый
ответ (если только что-то не выбьет систему из собственного состояния в дру-
гую суперпозицию). Невозможно точно сказать, в какое собственное состояние
система перейдет в момент наблюдения; это процесс, стохастический по своей
природе, и максимум, что мы можем сделать, — это присвоить вероятности
разным результатам.
Применим эту идею к нашей истории с Китти. Согласно копенгагенской
интерпретации, наше решение пронаблюдать, остановится она у миски с кор-
мом или у когтеточки, оказывает решающее влияние на волновую функцию,
как бы незаметно мы ни старались следить за кошкой. Когда мы не смотрим,
Китти находится в суперпозиции двух возможностей с равными амплитудами;
после того как она доходит до дивана или стола, мы складываем составляющие,
соответствующие каждому из промежуточных шагов, и обнаруживаем, что
происходит интерференция. Но когда мы решаем пронаблюдать за тем, какую
она выберет дорогу, это заставляет ее волновую функцию сколлапсировать.
Предположим, мы увидели, что Китти останавливается у когтеточки; как толь-
ко это наблюдение было выполнено, состояние кошки перестало быть супер-
позицией: она на 100 % находилась у когтеточки и на 0 % у миски. То же самое
произошло бы, если бы мы увидели ее у миски с кормом, но с противополож-
ными амплитудами. В любом случае возможностей для интерференции не 
Часть III. Энтропия и ось времени
остается, и ее волновая функция так или иначе эволюционирует в состояние,
обеспечивающее равные вероятности оказаться в конце путешествия на дива-
не и под столом.8
В связи с этим у нас есть хорошая новость и плохая. Хорошая новость за-
ключается в том, что это соответствует экспериментальным данным. Если
считать, что волновые функции коллапсируют каждый раз, когда мы выполня-
ем наблюдение, какую бы ненавязчивую стратегию наблюдения мы ни выбрали,
превращаясь в собственные состояния, связывающие 100-процентную вероят-
ность с увиденным нами результатом, то мы можем с уверенностью заявлять,
что способны объяснить любые квантовые явления, известные физикам.
Плохая же новость такова: в этом нет смысла. Что можно считать «наблю-
дением»? Может ли сама кошка совершить наблюдение? А неживой объект?
Определенно, мы не хотим верить в то, что такое явление, как сознание, каким-
то образом может играть ключевую роль в фундаментальных законах физики?
(Не хотим и не будем!) И действительно ли предполагаемый коллапс проис-
ходит мгновенно, — или все же постепенно, но просто очень быстро?
Необратимость
По сути, больше всего в копенгагенской интерпретации квантовой механики
нас беспокоит то, что «наблюдение» здесь рассматривается как совершенно
особый тип природного явления, требующий отдельного закона природы.
В классической механике все происходящее вокруг нас может быть объяснено
с помощью систем, эволюционирующих согласно законам Ньютона. Однако
если мы учитываем коллапс волновой функции как он описан выше, в квантовой
механике система эволюционирует согласно правилам двух совершенно разных
типов.
1. Когда мы не смотрим, волновая функция эволюционирует гладко и пред-
сказуемо. Роль, которую в классической механике играют ньютоновские
законы, в квантовой механике отводится уравнению Шрёдингера, действу-
ющему по абсолютно аналогичному сценарию. Зная состояние системы
в любой момент времени, мы можем применить уравнение Шрёдингера,
для того чтобы достоверно спрогнозировать ее развитие как по направлению
в будущее, так и по направлению в прошлое. Эволюция сохраняет инфор-
мацию и полностью обратима.
2. Когда мы выполняем наблюдение, волновая функция коллапсирует. Коллапс
происходит не гладко, он непредсказуем, и информация при этом не со- 
Глава 11. Квантовое время
храняется. Значение амплитуды (в квадрате), присвоенное каждому кон-
кретному результату, сообщает нам вероятность того, что волновая функция
перейдет в состояние, полностью сконцентрированное на этом результате.
Две разные волновые функции могут запросто сколлапсировать в одно и то
же состояние при условии, что наблюдение осуществляется; следовательно,
коллапс волновой функции необратим.
Безумие! Но это работает. В копенгагенской интерпретации мы берем
понятия, кажущиеся простым приближением к некоей глубинной базисной
истине, — проводя различие между «системой», представляющей собой
истинно квантовый механизм, и «наблюдателем», не выходящим за рамки
классической механики, — и воображаем, будто эти категории играют кри-
тическую роль в фундаментальной структуре реальности. Большинство
физиков, даже те, кто ежедневно применяет квантовую механику в своих
исследованиях, прекрасно понимают друг друга, разговаривая на языке ко-
пенгагенской интерпретации, и совершенно не беспокоятся о неловких во-
просах, которые она поднимает. Другие, особенно те, кто серьезно задумы-
вается об основах квантовой механики, убеждены, что нам необходимо нечто
более совершенное. К сожалению, единого мнения относительно того, как
могло бы выглядеть это более совершенное толкование, пока не выработано.
Для многих людей самое проблемное свойство квантовой механики — это
как раз крах безупречной предсказуемости (Эйнштейн один из них; именно
с этим связано его знаменитое высказывание о том, что «Бог не играет в ко-
сти со Вселенной»). Если копенгагенская интерпретация верна, то в кванто-
вом мире не может существовать такого явления, как демон Лапласа; во
всяком случае, пока этот мир включает наблюдателей. Акт наблюдения при-
вносит в эволюцию мира элемент истинной случайности. Не полностью
случайный (волновая функция может обеспечивать очень высокую вероят-
ность увидеть один какой-то результат и очень низкую — любые другие). Но
непреодолимо случайный, в том смысле, что не существует такой утерянной
информации, которая, попади она к нам в руки, позволила бы точно прогно-
зировать результаты.9 Великолепие и слава классической механики — это
отчасти следствие ее железобетонной надежности: даже если демон Лапласа
в действительности не существует, мы знаем, что, в принципе, он может су-
ществовать. Квантовая механика разрушает эту надежду. Людям потребова-
лось немало времени для того, чтобы привыкнуть к мысли о вероятности как
о еще одной неотъемлемой фундаментальной характеристике законов физи-
ки, и многим это понятие по сей день причиняет огромный душевный дис-
комфорт. 
Часть III. Энтропия и ось времени
Один из вопросов, которые мы задавали о стреле времени, — каким об-
разом нам примирить между собой необратимость макроскопических систем,
описываемых статистической механикой, с несомненной обратимостью микро-
скопических законов физики. Однако сейчас, когда мы узнали о квантовой
механике, создается впечатление, что микроскопические законы физики впол-
не могут оказаться необратимыми. Коллапс волновой функции — это процесс,
привносящий собственную стрелу времени в физические законы: волновые
функции коллапсируют, но расколлапсировать они не в состоянии. Если мы
наблюдаем за Китти и видим, что она на диване, то сразу же после выполнения
этого измерения мы понимаем, что она пребывает в собственном состоянии
(100 % на диване). Но нам неизвестно, в каком состоянии она была до того, как
мы провели измерение. Очевидно, что это информация была уничтожена. Мы
знаем лишь, что для того, чтобы кошка оказалась на диване, волновая функция
когда-то должна была иметь ненулевую амплитуду, — но мы не можем сказать,
каково было значение амплитуды, а также какие амплитуды соответствовали
другим возможным исходам, если таковые были.
Итак, коллапс волновой функции — если это действительно верная интер-
претация квантовой механики — определяет собственную стрелу времени.
Можно ли на ее основании как-то объяснить «главную» стрелу времени — тер-
модинамическую стрелу, присутствующую во втором начале термодинамики,
которую мы обвинили во всевозможных макроскопических отличиях прошлого
от будущего?
Вероятно, нет. Несмотря на то что необратимость — ключевая характери-
стика стрелы времени, не все необратимости одинаковы. И совершенно непо-
нятно, как один тот факт, что волновые функции коллапсируют, может объяснить
гипотезу о прошлом. Вспомните, о чем мы говорили: нетрудно понять, почему
энтропия увеличивается; трудно понять, почему она вообще когда-то была
низкой. Коллапс волновой функции не предлагает никакой помощи в понима-
нии этого вопроса.
С другой стороны, квантовая механика наверняка сыграет определенную
роль в окончательном объяснении стрелы времени, даже если внутренняя не-
обратимость коллапса волновой функции сама по себе напрямую проблему не
решает. В конце концов, мы верим, что законы физики по своей сути квантово-
механические. Именно квантовая механика устанавливает правила и диктует
нам, что разрешено, а что запрещено в нашем мире. Абсолютно естественно
ожидать, что эти правила включатся в действие, когда мы, наконец-то, начнем
понимать, почему у нашей Вселенной была такая низкая энтропия сразу после
Большого взрыва. Нам пока неизвестно наверняка, куда приведет нас это 
Глава 11. Квантовое время
путешествие, но мы достаточно сообразительны, для того чтобы предсказать,
какие инструменты точно пригодятся нам в дороге.
Неопределенность
В своем обсуждении волновых функций мы обходили молчанием одно крити-
чески важное свойство. Мы сказали, что волновые функции связывают ампли-
туду со всеми возможными результатами любого наблюдения, которое только
нам вздумается провести. В нашем мысленном эксперименте мы ограничились
только одним типом наблюдения — проверкой местоположения кошки —
и только двумя возможными результатами в каждый из интересующих нас
моментов времени. У реальной же кошки, или элементарной частицы, или яйца,
или любого другого объекта бесконечное число возможных положений, и со-
ответствующая волновая функция в каждом случае связывает амплитуду с лю-
бой из этих возможностей.
Еще важнее то, что мы можем измерять и другие вещи помимо положения.
Вспомнив свой опыт с классической механикой, мы можем предложить про-
наблюдать за импульсом, а не за положением кошки. И это также вполне до-
пустимо; состояние кошки описывается волновой функцией, которая присва-
ивает амплитуду каждому возможному значению импульса, которое мы можем
получить в процессе измерения. Когда мы выполняем такое измерение и полу-
чаем ответ, волновая функция коллапсирует в «собственное состояние импуль-
са», соответствующее ненулевой амплитуде только для одного определенного
значения импульса, — того самого, что мы только что фактически измерили.
Однако, можете подумать вы, если это верно, то что мешает нам поместить
кошку в состояние, в котором и ее положение и импульс определяются абсо-
лютно точно, то есть в обыкновенное классическое состояние? Другими сло-
вами, почему мы не можем взять кошку с произвольной волновой функцией,
измерить ее положение, для того чтобы оно приняло одно определенное зна-
чение, а затем измерить ее импульс, чтобы он также сколлапсировал в опреде-
ленное значение? В таком случае мы получим полностью определенное клас-
сическое состояние и все неопределенности будут отсутствовать.
Это невозможно, а причина в том, что не существует волновых функций,
одновременно сконцентрированных и вокруг одного-единственного значения
положения, и вокруг одного-единственного значения импульса. Действитель-
но, попытка найти такое состояние обречена на провал: если волновая функция
сконцентрирована около определенного значения положения, то амплитуды
будут максимально рассредоточены по всем возможным значениям импульса. 
Часть III. Энтропия и ось времени
И наоборот: если волновая функция сконцентрирована около определенного
импульса, она рассредоточена по всем возможным положениям. Получается,
что когда мы наблюдаем за положением объекта, мы теряем любую информацию
о его импульсе, и наоборот.10 (Если же мы измеряем положение лишь прибли-
зительно, а не точно, то мы можем сохранить некоторые сведения об импульсе;
именно это происходит при макроскопических измерениях, выполняемых
в реальном мире.)
В этом заключается истинный смысл принципа неопределенности Гейзен-
берга. В квантовой механике можно «точно знать» положение частицы —
более того, частица может находиться в собственном состоянии, то есть может
быть известно, что вероятность обнаружить ее в определенном положении
равна 100 %. Точно так же можно «точно знать» импульс частицы. Но невоз-
можно одновременно обладать информацией и о положении, и об импульсе.
Таким образом, измеряя величины, которыми система описывается в класси-
ческой механике, — одновременно и положение и импульс, — мы никогда не
можем заранее знать, каким будет результат. Это и есть принцип неопределен-
ности.
Принцип неопределенности подразумевает, что волновая функция должна
быть рассредоточена по возможным значениям либо положения, либо импуль-
са, либо (и чаще всего бывает именно так) обеих этих величин. Неважно, какую
систему мы рассматриваем, — проявление квантовой непредсказуемости при
попытке измерить ее свойства неизбежно. Две измеряемые величины допол-
няют друг друга: когда волновая функция сконцентрирована вокруг положения,
она рассредоточена по импульсу, и наоборот. Реальные макроскопические
системы, хорошо поддающиеся описанию в классическом пределе квантовой
механики, находятся в компромиссных состояниях, характеризующихся не-
большими неопределенностями как положений, так и импульсов. Для доста-
точно больших систем эта неопределенность относительно мала, поэтому мы
ее совершенно не замечаем.
Помните, что в действительности таких вещей, как «положение объекта»
или «импульс объекта», не существует — только волновая функция, назнача-
ющая определенные амплитуды возможным результатам наблюдения. Тем не
менее очень часто мы поддаемся соблазну перейти на язык квантовых флукту-
аций — мы говорим, что не можем связать объект с одним конкретным поло-
жением, потому что принцип неопределенности заставляет его немного флук-
туировать вокруг. Это неизбежный лингвистический огрех, но мы не слишком
уж чопорны и будем иногда позволять себе эту слабость, помня, однако, что
эта формулировка не способна в точности отразить действительность. Смысл 
Глава 11. Квантовое время
не в том, что существуют положение и импульс и каждая из этих величин не-
много колеблется, а в том, что существует волновая функция, которая не может
быть одновременно локализована и в положении, и в импульсе.
В следующих главах мы познакомимся с приложениями квантовой механи-
ки в намного более величественных системах, чем отдельные частицы или даже
отдельные кошки: с квантовой теорией поля, а также с квантовой гравитацией.
Тем не менее базовый каркас квантовой механики в любом случае останется
неизменным. Квантовая теория поля — это союз квантовой механики со спе-
циальной теорией относительности, описывающий частицы, которые мы видим
вокруг себя, — как наблюдаемые свойства более глубокой фундаментальной
структуры — квантовых полей. Принцип неопределенности не позволит нам
точно определить положение и импульс каждой частицы и даже точное число
частиц. Он же служит первоисточником «виртуальных частиц», которые по-
являются и исчезают даже в пустом пространстве, и в конечном итоге приводит
к хокинговскому излучению черных дыр.
А квантовая гравитация — это штука, которую мы вообще не понимаем.
Общая теория относительности предлагает чрезвычайно успешное описание
гравитации в том виде, как мы ее воспринимаем по ее воздействию на окружа-
ющий мир, но эта теория построена на классическом фундаменте. Гравитация —
это искривление пространства—времени, и, в принципе, в наших силах из-
мерить искривление пространства—времени с любой степенью точности.
Практически никто не сомневается, что это всего лишь приближение к более
полной теории квантовой гравитации, в которой само пространство—время
описывается волновой функцией, связывающей разные амплитуды с разными
значениями искривления. Возможно даже, что целые вселенные появляются
и исчезают в точности как виртуальные частицы. Но в попытках сконструиро-
вать полную теорию квантовой гравитации мы натыкаемся на трудно преодо-
лимые препятствия — как технические, так и философские. Преодоление этих
препятствий — ежедневный труд большого числа физиков.