В многофакторных моделях результативный признак зависит от нескольких факторов. Множественный или многофакторный корреляционно-регрессионный анализ решает три задачи: определяет форму связи результативного признака с факторными, выявляет тесноту этой связи и устанавливает влияние отдельных факторов. Для двухфакторной линейной регрессии эта модель имеет вид:
| (2.15) |
Параметры модели ao, a1, a2 находятся путем решения системы нормальных уравнений:
| (254) |
Покажем особенности эконометрического многофакторного анализа на рассмотренном выше примере, но введем дополнительный фактор – размер семьи. В таблице 6 представлены статистические данные о расходах на питание, душевом доходе и размере семьи для девяти групп семей. Требуется проанализировать зависимость величины расходов на питание от величины душевого дохода и размера семьи.
Таблица52
| Номер группы | Расход на питание (у) | Душевой доход (х) | Размер семей (чел) |
| 1,5 | |||
| 2.1 | |||
| 2.7 | |||
| 3.2 | |||
| 3.4 | |||
| 3.6 | |||
| 3,7 | |||
| 4,0 | |||
| 3.7 |
Рассмотрим двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (x1) и размера семей (x2). Результаты расчетов с использованием электронных таблиц EXCEL представлены в таблице 7.
Таблица 53
| ВЫВОД ИТОГОВ | |||||
| Регрессионная статистика | |||||
| Множественный R | 0,997558 | ||||
| R-квадрат | 0,995121 | ||||
| Нормированный R-квадрат | 0,993495 | ||||
| Стандартная ошибка | 50,84286 | ||||
| Наблюдения | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 611,9239 | 1,1612E-07 | |||
| Остаток | 15509,98 | 2584,996 | |||
| Итого | |||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | |
| Y-пересечение | -187,141 | 77,17245 | -2,42498 | 0,051513 | -375,97561 |
| Переменная X 1 | 0,071995 | 0,004463 | 16,13289 | 3,61E-06 | 0,06107576 |
| Переменная X 2 | 343,0222 | 29,40592 | 11,66507 | 2,39E-05 | 271,068413 |
Эконометрическая модель имеет следующий вид
Высокие значения коэффициента детерминации R2 = 0,995 и значение F – критерия однозначно говорит об адекватности полученной модели исходным данным. Необходимо отметить, что эти значения намного превышают значения R2 и F – критерия, которые были получены в модели с одним фактором. Таким образом, введение в модель еще одного фактора улучшает качество модели в целом.
В какой степени допустимо использовать критерий R2 для выбора между несколькими регрессионными уравнениями? Дело в том, что при добавлении очередного фактора R2 всегда возрастает и, если взять число факторов, равным числу наблюдений, то можно добиться того, что R2 = 1. Но это вовсе не будет означать, что полученная эконометрическая модель будет иметь экономический смысл.
Попыткой устранить эффект, связанный с ростом R2 при возрастании числа факторов, является коррекция значения R2 с учетом используемых факторов в нашей модели.
Скорректированный (adjusted) R2 имеет следующий вид:
(255)
где n – объем выборки;
k – количество коэффициентов в уравнении регрессии.
Для нашего случая
(256)
В определенной степени использование скорректированного коэффициента детерминации R2 более корректно для сравнения регрессий при изменении количества факторов.
В том случае, когда имеются одна независимая и одна зависимая переменные, естественной мерой зависимости является (выборочный) коэффициент корреляции между ними. Использование множественной регрессии позволяет обобщить это понятие на случай, когда имеется несколько независимых переменных. Корректировка здесь необходима по следующим очевидным соображениям. Высокое значение коэффициента корреляции между исследуемой зависимой и какой-либо независимой переменной может, как и раньше, означать высокую степень зависимости, но может быть обусловлено и другой причиной. Например, может существовать третья переменная, которая оказывает сильное влияние на две первые, что и является, в конечном счете, причиной их высокой коррелированности. Поэтому возникает естественная задача найти «чистую» корреляцию между двумя переменными, исключив (линейное) влияние других факторов. Это можно сделать с помощью коэффициента частной корреляции:
| (2.18) |
где
(257)
(258)
(259)
Значения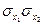 
вычисляются как
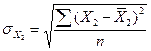(260)
Значения коэффициента частной корреляции лежат в интервале [-1,1], как у обычного коэффициента корреляции. Равенство этого коэффициента нулю означает, говоря нестрого, отсутствие прямого (линейного) влияния переменной X1 на У.
Существует тесная связь между коэффициентом частной корреляции и коэффициентом детерминации, а именно
| (261) |
или
(262)
Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае линейной двухфакторной модели рассчитываются по формулам:
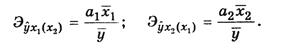(263)
Черта над символом, как и ранее, означает среднюю арифметическую. Частные коэффициенты эластичности показывают, насколько процентов изменится результативный признак, если значение одного из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным.
Для определения области возможных значений результативного показателя при известных значениях факторов, т.е. доверительного интервала прогноза, необходимо учитывать два возможных источника ошибок. Ошибки первого рода вызываются рассеиванием наблюдений относительно линии регрессии, и их можно учесть, в частности, величиной среднеквадратической ошибки аппроксимации изучаемого показателя с помощью регрессионной модели (Sy)
(264)
Ошибки второго рода обусловлены тем, что в действительности жестко заданные в модели коэффициенты регрессии являются случайными величинами, распределенными по нормальному закону. Эти ошибки учитываются вводом поправочного коэффициента при расчете ширины доверительного интервала; формула для его расчета включает табличное значение t-статистики при заданном уровне значимости и зависит от вида регрессионной модели. Для линейной однофакторной модели величина отклонения от линии регрессии задается выражением (обозначим его R):
, (265)
где п – число наблюдений,
L – количество шагов вперед,
а – уровень значимости прогноза,
X – наблюдаемое значение факторного признака в момент t,
– среднее значение наблюдаемого фактора,
– прогнозное значение фактора на L шагов вперед.
Таким образом, для рассматриваемой модели формула расчета нижней и верхней границ доверительного интервала прогноза имеет вид:
| (266) |
где UL означает точечную прогнозную оценку изучаемого результативного показателя по модели на L шагов вперед.
