Вероятность события 
равна отношению числа m исходов испытаний, благоприятствующих наступлению события 
, к общему числу n всех равновозможных несовместных исходов, т.е.
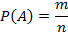
Следовательно, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, подсчитать все возможные несовместные исходы n, выбрать число интересующих нас исходов m и вычислить отношение m к n.
Свойства вероятностей: Вероятность достоверного события равна единице.
Вероятность невозможного события равна нулю.
Вероятность случайного события принимает значения от 0 до 1.
Сложение вероятностей
Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них. Обозначается 
.
Теорема сложения вероятностей несовместных событий: Вероятность суммы несовместных событий равна сумме вероятностей этих событий:
Следствие 1: Если события 
образуют полную систему, то сумма вероятностей этих событий равна единице.
Следствие 2: Сумма вероятностей противоположных событий равна единице.
Теорема сложения вероятностей совместных событий: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Умножение вероятностей
Вероятность наступления события А, вычисленная при условии наступления другого события В, называется условной вероятностью события А по отношению к событию В. Обозначается 
.
Событие А называется независимым от события В, если наступление события В не оказывает никакого влияния на вероятность наступления события А.
Произведением конечного числа событий называется событие, состоящее в том, что каждое из них произойдет. Обозначается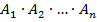 
.
Теорема умножения вероятностей независимых событий: Вероятность произведения независимых событий равна произведению вероятностей этих событий:
Теорема умножения вероятностей зависимых событий: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:
Формула полной вероятности
Пусть события (гипотезы) 
образуют полную группу событий и при наступлении каждого из них событие может наступить с некоторой условной вероятностью 
. Тогда вероятность наступления события равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события :
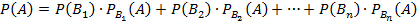
Формула Бернулли
Пусть проводится серия одинаковых независимых испытаний, в результате каждого из которых некое интересующее нас событие может появиться с определенной вероятность 
(одной и той же во всех испытаниях). Вероятность того, что в n независимых испытаниях событие наступит ровно 
раз (безразлично, в какой последовательности), находится по формуле Бернулли:
Примеры решения задач
Пример 1. Из слова "математика" выбирается наугад одна буква. Какова вероятность того, что это будет буква "а"?
Решение: Событие - наугад выбирается буква «а»
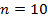- количество всех исходов
- количество благоприятствующих исходов (выбирается буква «а»)
Ответ: 0,3.
Во многих задачах на определение вероятности большее затруднение вызывает подсчёт числа вариантов возможных благоприятных исходов. Здесь на помощь приходят знания комбинаторики.
Пример 2. В ящике лежат одинаковые на ощупь 20 шаров. Из них 12 белых и 8 чёрных. Наугад вынимают два шара. Какова вероятность того, что они оба белые?
Решение: Событие - вынули два белых шара.
Число всех возможных событий равно числу сочетаний из 20 по 2: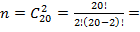 
.
Число благоприятных исходов равно числу сочетаний из 12 по 2: 
Ответ: 0,35.
Пример 3. В урне 4 белых и 6 черных шаров. Случайным образом вынули 1 шар. Какова вероятность того, что он белый?
Решение: Событие - вынули белый шар
- количество всех исходов
- количество благоприятствующих исходов
Ответ: 0,4.
Пример 4. В первой урне находятся 6 черных и 4 белых шара, во второй – 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми?
Решение: Событие 
вынутый из первой урны шар белый, событие 
вынутый из второй урны шар белый. События 
независимы, поэтому
Ответ: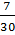 
.
Пример 5. Часы одной марки изготавливаются на трех заводах и поступают в магазин. Первый завод производит 20% всей продукции, второй - 30%, третий - 50%. В продукции первого завода спешат 5% всех часов, второго - 3%, третьего - 2%. Какова вероятность того, что купленные в магазине часы спешат?
Решение: Обозначим событие купленные часы спешат. Возможны гипотезы: 
часы изготовлены на первом заводе, 
; 
часы изготовлены на втором заводе, 
; 
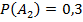часы изготовлены на третьем заводе,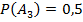 
. Найдем условные вероятности наступления события при осуществлении каждой из гипотез:
вероятность того, что купленные часы спешат, при условии, что они изготовлены на первом заводе;
вероятность того, что купленные часы спешат, при условии, что они изготовлены на втором заводе;
вероятность того, что купленные часы спешат, при условии, что они изготовлены на третьем заводе.
По формуле полной вероятности получаем:
Ответ: 0,029.
Пример 6. Вероятность попадания в цель при одном выстреле составляет 
. Найти вероятность четырех попаданий при шести выстрелах.
Решение: По условию задачи 
. По формуле Бернулли находим:
Ответ: 0,246.
