1) 
2) 
3) 
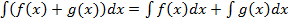
4) 
, где 
число
Таблица простейших интегралов
1) 
| 8) 
|
2) 
| 9) 
|
3) 
| 10)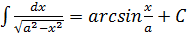 
|
4) 
| 11) 
|
5) 
| 12) 
|
6) 
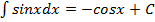
| 13) 
|
7) 
|
Основные методы интегрирования: непосредственное интегрирование, метод подстановки, интегрирование по частям
1. Непосредственное интегрирование основано на прямом использовании таблицы интегралов и основных свойств.
Пример 1. Найти интеграл:
а) 
Решение: Воспользуемся 3 и 4 свойствами неопределенных интегралов и формулами 1 и 2 из таблицы интегралов:
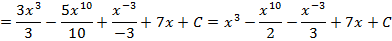
б)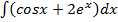 
Решение: Воспользуемся 3 и 4 свойствами неопределенных интегралов и формулами 4 и 7 из таблицы интегралов:
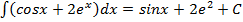
в) 
Решение: Почленно выполнив деление и применив 3 и 4 свойства неопределенных интегралов и формулы 1, 2 и 3 из таблицы интегралов, получим:
г) 
Решение: Воспользуемся определением степени с дробным показателем (
и правилами действий над степенями, преобразуем подынтегральное выражение, а затем применим 1 свойство неопределенных интегралов и формулу 2 из таблицы:
2. Интегрирование методом замены переменной (подстановкой) заключается в следующем: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения (не считая постоянного множителя).
Правило интегрирования подстановкой:
1) Определяют, к какому табличному интегралу приводится данный интеграл.
2) Определяют какую часть подынтегральной функции заменить новой переменной, и записывают замену.
3) Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной через дифференциал новой переменной.
4) Производят замену под интегралом.
5) Находят полученный интеграл.
6) Производят обратную замену.
Пример 2. Найти интеграл методом замены переменной:
а) 
б) 
в) 
3. Интегрирование по частям. Интегрируя обе части равенства 
, получим 
или 
, откуда получаем:
Это формула интегрирования по частям. При интегрировании по частям данное подынтегральное выражение представляют в виде произведения двух сомножителей, которые обозначают 
и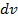 
. Множитель стараются выбрать так, чтобы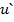 
было проще, чем .
Пример 3. Проинтегрировать по частям:
а) 
б) 
Определенный интеграл. Формула Ньютона-Лейбница
Определение: Если 
первообразная функция для 
, то приращение 
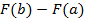первообразных функций при изменении аргумента 
от 
до 
называется определенным интегралом и обозначается символом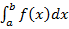 
, то есть
где 
нижний предел, 
верхний предел определенного интеграла. Это равенство называется формулой Ньютона-Лейбница.
Свойства определенного интеграла
1.) 
2.) 
3.) 
4.) 
5.) 
