Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида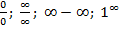 
. Для раскрытия неопределенностей можно воспользоваться следующими приемами:
1. Если получаем 
, где 
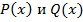– многочлены, то в этом случае надо числитель и знаменатель разложить на множители и сократить на 
, а затем опять подставить предельное значение.
2. Если получаем неопределенность 
и есть иррациональность, то числитель и знаменатель надо домножить на сопряженную величину.
3. Если при 
получаем неопределенность 
, то надо числитель и знаменатель почленно разделить на неизвестное слагаемое в наивысшей степени.
4. Если получаем неопределенность 
, а 
представлена в виде разности двух дробей, то необходимо привести дробь к общему знаменателю и получить неопределенность 
.
5. Если получаем неопределенность и есть иррациональность, то числитель и знаменатель домножаем на сопряженное выражение.
6. Первый замечательный предел раскрывает неопределенность вида и имеет вид:
Следствия: 
7. Второй замечательный предел раскрывает неопределенность вида 
и имеет вид:
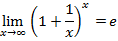
Следствия: 
Примеры решения задач
Пример 1. Вычислить значение предела:
1. 
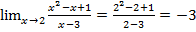
2. 
, так как 
, то 
при 
есть величина бесконечно малая, а обратная ей величина 
бесконечно большая.
3. 
. При подстановке предельного значения получаем неопределенность 
, значит необходимо разложить числитель и знаменатель на множители и после сокращения вычислить предел. При разложении воспользуемся формулой из школьного курса: если 
и 
- корни квадратного трехчлена, то 
.
Имеем: 
4. 
. Получаем неопределенность , умножим числитель и знаменатель на величину, сопряженную числителю, то есть на 
и затем, сократив дробь, получим:
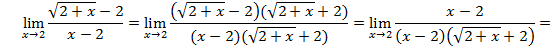
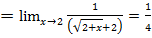
5. 
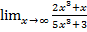. Получаем неопределенность 
, разделим почленно числитель и знаменатель на 
, затем воспользуемся теоремами о пределах и определением бесконечно малых величин:
6. 
. Имеем неопределенность вида 
, приведем дроби к общему знаменателю, сократим полученную дробь и вновь подставим предельное значение:
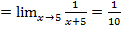
7. 
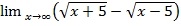. Получаем неопределенность , умножим и разделим на величину, сопряженную данному выражению:
8. 
. Получаем неопределенность вида . С помощью преобразований сведем данный предел к первому виду первого замечательного предела:
, так как 
и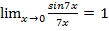 
(следствие (2) из первого замечательного предела).
9. 
. Получаем неопределенность вида . С помощью преобразований сведем данный предел к виду второго замечательного предела:
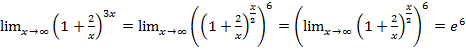, так как 
(следствие (2) из второго замечательного предела).
