Определение: Ряд называется знакочередующимся, если всякие два соседних члена ряда являются числами разных знаков.
Будем для определенности предполагать, что первый член ряда положителен.
Теорема (признак Лейбница): Если знакочередующийся ряд удовлетворяет условиям: 1) последовательность его членов монотонно убывает по абсолютной величине; 2) общий член ряда стремится к нулю, то ряд сходится.
Функциональные ряды. Степенные ряды
Определение: Функциональным рядом называют сумму членов функциональной последовательности 
.
Зафиксируем некоторое значение 
, в результате получим обычный числовой ряд, который можно исследовать на сходимость.
Из всех функциональных рядов одними из наиболее распространенных являются так называемые степенные ряды.
Определение: Степенным рядом называется ряд вида:
где числа 
называют коэффициентами ряда, а член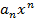 
- общим членом ряда.
Определение: Число 
называется радиусом сходимости ряда
, если при 
ряд сходится и притом абсолютно, а при 
ряд расходится.
Радиус сходимости можно найти, используя признак Даламбера:
( не зависит от n),
Отсюда следует, что если существует предел 
, то радиус сходимости равен этому пределу и ряд сходится при 
, то есть в промежутке 
, который называется интервалом сходимости.
Если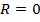 
, то ряд сходится в единственной точке 
.
Сходимость ряда при 
и 
исследуется с помощью какого-либо из признаков сходимости.
Примеры решения задач
Пример 1. Найти промежуток сходимости степенного ряда
Решение:
Используя формулу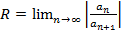 
, получим:
Следовательно, данный ряд сходится абсолютно при 
Исследуем сходимость ряда в точках 
и 
. При имеем ряд
Это знакочередующийся ряд, который в силу признака Лейбница сходится.
При имеем ряд
или
Это обобщенный гармонический ряд, который расходится, так как 
Отсюда следует, что данный ряд сходится при 
.
Ответ: .
Раздел 2. Основы теории вероятностей и математической статистики
Тема 2.1
Вероятность. Закон распределения дискретной случайной величины. Характеристики случайной величины
Элементы комбинаторики
Определение: Произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут:
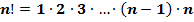
Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов.
В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.
1. Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками. Число перестановок обозначается 
и вычисляется по формуле:
2. Размещениями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком из расположения. Число размещений обозначается 
и вычисляется по формуле:
- размещения без повторений
- размещения с повторениями
3. Сочетаниями называются все возможные комбинации из n элементов по k, которые отличаются друг от друга по крайней мере хотя бы одним элементом. Число сочетаний обозначается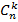 
. Число сочетаний вычисляется по формуле: 
При решении задач комбинаторики используют следующие правила:
Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m 
n способами.
Основные понятия и теоремы теории вероятностей
Событие – исход наблюдения или эксперимента. Обозначаются события заглавными буквами латинского алфавита A, B, C, D.
Событие называется достоверным, если в результате данного испытания оно обязательно произойдет.
Событие называется невозможным, если в результате данного испытания оно произойти не может.
Событие называется случайным, если в результате данного испытания оно может произойти или не произойти.
События называются совместными, если появление одного из них не исключает появления другого. События называются несовместными, если появление одного из них исключает появление другого.
Полной системой событий 
, 
, 
,…. 
называется совокупность несовместных событий, наступление одного из которых обязательно при данном испытании. Если полная система состоит из двух несовместных событий, то такие события называются противоположными. Событие, противоположное событию 
, обозначается 
.
Число, являющееся выражением меры объективной возможности наступления события А, называется вероятностью этого события и обозначается символом P (А).
